
- •3.1. Тензор напряжений
- •3.2. Тензор дисторсии
- •3.3. Изометрическое преобразование
- •3.4. Тензор деформации
- •3.5. Лабораторная система отсчета и
- •3.6. Проблема факторизации
- •3.7. Подходы Лагранжа и Эйлера. Другие тензоры деформаций
- •3.8. Тензор малых деформаций.
- •3.10 Простейшие модели физических (механических) свойств среды. Закон Гука
- •3.10.1. Изотропное тело
- •3.10.2. Ортотропный материал
- •3.10.3. Трансверсально изотропное тело
- •3.11. Виртуальная и действительная работа напряжений
- •3.12 Геометрические и массовые характеристики
3.4. Тензор деформации
Рассмотрим
другой частный случай: тензор А
симметричен, симметричен и тензор
дисторсии. Будем их обозначать в этом
случае
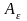 и
и
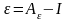 , (3.10)
, (3.10)
тензор назовем тензором деформации (в механике рассматривают и другие тензоры, называемые также тензорами деформации). Как и любой симметричный тензор, тензор имеет три главных направления
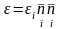 , (3.11)
, (3.11)
эти направления совпадают с главными направлениями аффинора
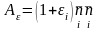 . (3.12)
. (3.12)
В случае
одноосной деформации
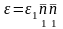 преобразование (3.8) принимает вид
преобразование (3.8) принимает вид
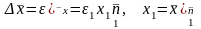 . (3.13)
. (3.13)
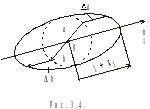
На рис. 3.2
штриховой линией показана совокупность
начальных положений единичных волокон;
эллипс – положения концов этих волокон
после деформирования; начала волокон
считаются неподвижными. Смещение концов
всех волокон, как видно из выражения
(13), параллельны оси
.
Волокна ортогональные
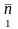 не деформируются и не поворачиваются;
волокна, параллельные
,
удлиняются; их относительное удлинение
(
не деформируются и не поворачиваются;
волокна, параллельные
,
удлиняются; их относительное удлинение
( )
равно
)
равно
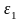 .
.
 Остальные
волокна и удлиняются, и поворачиваются.
Стержень с осью
вытягивается, удлиняется
Остальные
волокна и удлиняются, и поворачиваются.
Стержень с осью
вытягивается, удлиняется
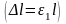 ,
поперечные сечения остаются плоскими,
поперечными, недеформированными.
,
поперечные сечения остаются плоскими,
поперечными, недеформированными.
В случае плоской деформации
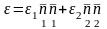 ,
,
если главные
деформации имеют одинаковые знаки,
недеформированными остаются лишь
волокна, ортогональные плоскости
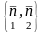 .
Круг в этой плоскости также превращается
в эллипс с главными осями
.
Круг в этой плоскости также превращается
в эллипс с главными осями
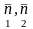 .
Если
.
Если
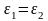 ,
то круг остается кругом и волокна в
плоскости
не поворачиваются.
,
то круг остается кругом и волокна в
плоскости
не поворачиваются.
В отличии от
тензора деформации, ранг аффинора
всегда равен 3 и его главные значения
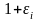 положительны.
Определитель
положительны.
Определитель
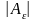 представляет отношение нового объема
тела к начальному и равен
представляет отношение нового объема
тела к начальному и равен
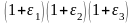 .
.
3.5. Лабораторная система отсчета и
В общем случае аффинор А не симметричен и не ортогонален. Сфера преобразуется в эллипсоид, но главные оси эллипсоида не являются главными направлениями аффинора. Происходит и деформирование тела, и его поворот.
О “физической” стороне дела будет сказано ниже, но сейчас полезно отметить, что деформацию инициирует тензор напряжений, тогда как поворот не требует усилий; он связан лишь с условиями закрепления тела. Поэтому при записи “физических ” соотношений используют термины “напряжения” и “деформации”, оставляя в стороне поворот. Отсюда следует необходимость решения задачи: как, зная тензор А, определить тензор .
Любое
преобразование можно рассматривать
как совокупность нескольких преобразований.
Например, если
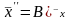 ,
,
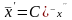 ,
то
,
то
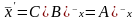 ;
аффинор представляет произведение двух
аффиноров. Разбиение на два не означает,
что сначала произошло деформирование
В, затем С; просто это могло произойти
в такой последовательности. Если одно
из движений (В или С) представляло жесткий
поворот, то с точки зрения физических
особенностей процесса не важно, был ли
поворот после деформирования или в
процессе деформирования: поворот на
процесс не влияет. Возможно разложение
и на большее число движений, но практический
смысл имеет только такое разложение:
деформация без поворота и поворот без
деформации.
;
аффинор представляет произведение двух
аффиноров. Разбиение на два не означает,
что сначала произошло деформирование
В, затем С; просто это могло произойти
в такой последовательности. Если одно
из движений (В или С) представляло жесткий
поворот, то с точки зрения физических
особенностей процесса не важно, был ли
поворот после деформирования или в
процессе деформирования: поворот на
процесс не влияет. Возможно разложение
и на большее число движений, но практический
смысл имеет только такое разложение:
деформация без поворота и поворот без
деформации.
Итак, имея тензор А, можно представить два варианта развития событий:
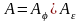 (3.14)
(3.14)
(деформация, затем поворот) или, наоборот,
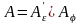 (3.15)
(3.15)
(рис. 3.3).
Ориентиром на этих рисунках служат
главные оси деформаций: эти волокна
поворачиваются только в связи с жестким
поворотом тела. Нетрудно видеть, что в
обоих случаях поворот одинаков и
отображается одним и тем же тензором
,
но аффиноры деформаций
и
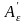 характеризуются одними и теми же главными
деформациями, но различными главными
направлениями (повернутыми друг
относительно друга на угол ).
Умножив А в обоих выражениях на
характеризуются одними и теми же главными
деформациями, но различными главными
направлениями (повернутыми друг
относительно друга на угол ).
Умножив А в обоих выражениях на
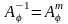 ,
получим
,
получим
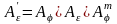 ; (3.16)
; (3.16)
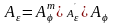 (3.17)
(3.17)
т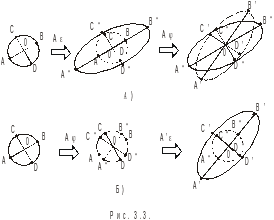 ензоры
и
различны. Итак, к проблеме факторизации
добавляется еще одна: какой из этих
тензоров –
или
– использовать в физических соотношениях.
ензоры
и
различны. Итак, к проблеме факторизации
добавляется еще одна: какой из этих
тензоров –
или
– использовать в физических соотношениях.
Несколько
забегая вперед (в “физику”), представим
себе, что рассматриваемое тело линейно
упруго и изотропно, вдобавок коэффициент
Пуассона равен
нулю. Тогда, как увидим, закон Гука примет
вид
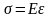 .
Это означает, что главные оси напряжений
и деформаций совпадают. Но в рассмотренном
в п. 5.1 напряженном состоянии речь шла
о деформированном теле; главные оси
тензора на рис. 3.3
должны отвечать направлениям
.
Это означает, что главные оси напряжений
и деформаций совпадают. Но в рассмотренном
в п. 5.1 напряженном состоянии речь шла
о деформированном теле; главные оси
тензора на рис. 3.3
должны отвечать направлениям
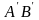 и
и
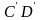 ,
которые совпадают с главными деформациями
тензора
.
Значит, закон Гука имеет вид
,
которые совпадают с главными деформациями
тензора
.
Значит, закон Гука имеет вид
 .
.
С другой стороны если идет речь о неупругом деформировании, то важно не только текущее значение деформации, но и ее история. Если представить себе испытания образца на вращающейся платформе, то испытатель (на платформе) увидит деформацию , а посторонний наблюдатель (не вращающий с платформой) – . История деформаций для этих наблюдателей различно, но лишь для испытателя она верна: образец никак не реагирует на движение платформы. Для неупругого тела правильнее выделять в теле тензор , но при записи физических соотношений тензор уже нельзя использовать: его главные оси зависят от поворота . Поэтому тензор следует пересчитать в “лабораторную” систему, незамечающую :
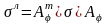 . (3.18)
. (3.18)
