
- •3.1. Тензор напряжений
- •3.2. Тензор дисторсии
- •3.3. Изометрическое преобразование
- •3.4. Тензор деформации
- •3.5. Лабораторная система отсчета и
- •3.6. Проблема факторизации
- •3.7. Подходы Лагранжа и Эйлера. Другие тензоры деформаций
- •3.8. Тензор малых деформаций.
- •3.10 Простейшие модели физических (механических) свойств среды. Закон Гука
- •3.10.1. Изотропное тело
- •3.10.2. Ортотропный материал
- •3.10.3. Трансверсально изотропное тело
- •3.11. Виртуальная и действительная работа напряжений
- •3.12 Геометрические и массовые характеристики
3.1. Тензор напряжений
Итак, дано тело произвольных размеров и формы; известно, что оно неподвижно но и нагружено внешними силами так, что во всех его элементарных объемах на одинаковых площадках действуют одинаковые силы. Такое напряженное состояние тела называют однородным. Для рассмотрения напряжений в нем можно выбрать любую его часть любой формы и размера. Исследуется статическая сторона явления: удобно считать тело твердым, хотя анализ справедлив для любой Среды. Ключом к рассмотрению является известный метод сечений.
Напомним, что
напряжением
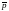 называют интенсивность силы, передающейся
через некоторую площадку (с единичной
нормалью
называют интенсивность силы, передающейся
через некоторую площадку (с единичной
нормалью
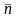 )
от одной части тела к другой, отделенной
мысленно этой площадкой. Однородность
означает, что вектор
(интенсивность
силы, распределенной по площади,
измеряемая в Паскалях) зависит только
от ориентации площадки
.
По третьему закону Ньютона на площадке
с нормалью –
(обычно рассматривается наружная
нормаль) напряжение равно –
.
Через точку тела можно провести
бесчисленное множество площадок;
напряжения на них также представляют
бесчисленное множество векторов, но
эти множество, как увидим ниже, упорядочено.
)
от одной части тела к другой, отделенной
мысленно этой площадкой. Однородность
означает, что вектор
(интенсивность
силы, распределенной по площади,
измеряемая в Паскалях) зависит только
от ориентации площадки
.
По третьему закону Ньютона на площадке
с нормалью –
(обычно рассматривается наружная
нормаль) напряжение равно –
.
Через точку тела можно провести
бесчисленное множество площадок;
напряжения на них также представляют
бесчисленное множество векторов, но
эти множество, как увидим ниже, упорядочено.
Чтобы выделить
полностью часть тела, минимально
требуется провести четыре сечения,
получив тем самым четырехгранник с
наружными нормалями
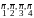 .
Силы, действующие по этим граням,
находятся умножением напряжений
.
Силы, действующие по этим граням,
находятся умножением напряжений
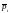 (постоянных на каждой грани) по площади
граней
(постоянных на каждой грани) по площади
граней
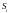 .
Из геометрических соображений следует,
что эти площади связаны между собой и
достаточно знать
.
Из геометрических соображений следует,
что эти площади связаны между собой и
достаточно знать
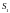 ,
чтобы, по нормалям
,
чтобы, по нормалям
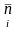 найти все
(в
разделе 4 будет показано, что для любого
многогранника сумма
найти все
(в
разделе 4 будет показано, что для любого
многогранника сумма
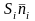 равна нулю).
равна нулю).
Неподвижность тела при действии этих сил требует, чтобы суммарная сила была равна нулю
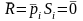 (i=1…4).
(i=1…4).
Таким образом,
достаточно знать три напряжения на
каких-либо трех площадках
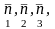 чтобы найти четвертое:
чтобы найти четвертое:

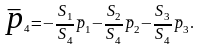 (3.1)
(3.1)
Как видим,
вектор
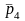 представляет линейную форму трех
векторов
представляет линейную форму трех
векторов
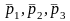 ,
коэффициенты которой зависят только
от векторов
.
,
коэффициенты которой зависят только
от векторов
.
Варьируя положение четвертой площадки, найдем напряжения на всех площадках. Следовательно, напряженное состояние однозначно определяется векторами и (i=1…3).
Удобнее всего
для этой цели использовать три
ортогональные площадки, обозначим их
нормали
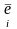 (они послужат ортами декартова базиса),
четвертую – просто
,
ее площадь – S. Легко
установить, что
(они послужат ортами декартова базиса),
четвертую – просто
,
ее площадь – S. Легко
установить, что
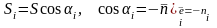
(например, из
упомянутого выше условия
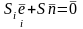 ),
и выражение (3.1) примет вид
),
и выражение (3.1) примет вид
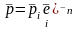 ,
i=1…3 (3.2)
,
i=1…3 (3.2)
Объект
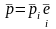 ,
представляющий, как мы знаем, двухвалентный
тензор, обозначают
и называют тензором напряжений. Выражение
(3.2) показывает смысл этого тензора: его
проекция на нормаль к любой площадке
определяет напряжение на этой площадке.
В частности, это относится и к площадкам
(
,
представляющий, как мы знаем, двухвалентный
тензор, обозначают
и называют тензором напряжений. Выражение
(3.2) показывает смысл этого тензора: его
проекция на нормаль к любой площадке
определяет напряжение на этой площадке.
В частности, это относится и к площадкам
(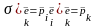 ).
Таким образом, напряжение
).
Таким образом, напряжение
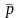 на площадке
представляет линейную функцию
с оператором .
Столбцами матрицы
являются векторы
на площадке
представляет линейную функцию
с оператором .
Столбцами матрицы
являются векторы
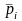 и, таким образом,
и, таким образом,
 – касательное напряжение на второй, а
не на первой площадке.
– касательное напряжение на второй, а
не на первой площадке.
При получении
тензора мы
использовали лишь одно условие равновесия
(по силам); в действительности их два.
Второе условие – по моментам – запишем
для куба со стороной а. Пара сил на
площадках
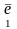 и
и
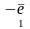 создают момент
создают момент
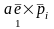 ,
аналогично найдутся еще два; сумма
моментов
,
аналогично найдутся еще два; сумма
моментов
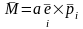 должна быть равна нулю. Отсюда
должна быть равна нулю. Отсюда
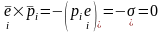 ,
,
то есть тензор симметричен. В сопротивлении материалов это условие называют законом парности касательных напряжений (12=21, 13=31, 23=32).
Простейшее напряженное состояние – одноосное, когда тензор сводится к диаде
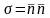 , (3.3)
, (3.3)
ранг его равен единице. Нетрудно видеть, что ранг матриц
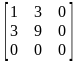 ,
,
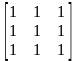 ,
,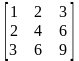
равен единице, значит, все они представляют координаты тензора (3.3) в различных декартовых базисах. Векторы на любых площадках коллинеарны.
Плоскому напряженному состоянию отвечают тензоры второго ранга; они приводятся к виду
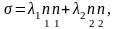
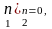 (3.4)
(3.4)
i – главные напряжения (вместе с =0),
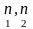 – главные направления тензора.
– главные направления тензора.
В механике
жидкостей наиболее популярно шаровое
напряженное состояние
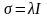 ,
величину , обычно
положительную, обозначают p
и называют давлением. Из простейших
состояний можно еще упомянуть чистый
сдвиг (
,
величину , обычно
положительную, обозначают p
и называют давлением. Из простейших
состояний можно еще упомянуть чистый
сдвиг (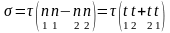 ,
,
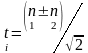 ,
плоское напряженное состояние) и
цилиндрическое (
,
плоское напряженное состояние) и
цилиндрическое (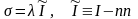 ).
).
