Структурные функции.

Понятие структурной функции часто применяется для анализа сред со случайными неоднородностями. Оно было введено акад. А.Н. Колмогоровым для описания поля скоростей турбулентных движений воздушных масс в атмосфере.

По определению, структурная функция представляет величину

, (64)

то есть средний квадрат разности значений случайной величины в двух точках. Пусть в точке 1 скорость является случайной величиной и равна , а в точке 2 - . Тогда структурная функция будет характеризовать связь между скоростями в двух точках.

Рассмотрим структурную функцию некоторого стационарного процесса. При этом несущественно, по времени или по пространству производится сдвиг.

. (65)

Это выражение дает связь между корреляционной и структурной функциями и показывает, что для стационарного процесса возможно использование как той, так и другой.

Корреляционная функция в максимуме равна квадрату дисперсии. Следовательно, . То есть корреляционная функция в нуле принимает максимальное значение, структурная – минимальное. На корреляционная функция равна нулю, структурная . Поскольку , получаем:

. (66)

Мы показали, что .

Следовательно, для стационарного процесса получаем еще одну формулу, связывающую корреляционную и структурную функции:

. (67)

Некоторые исследования, связанные с ограничением интервала усреднения, показывают:

1. Корреляционная функция дает большую статистическую точность, если исследуемый объем состоит из множества мелких неоднородностей.

2. Если неоднородности крупные, большую статистическую точность дают структурные функции.

Стационарные случайные процессы

Случайный процесс называется стационарным, если одномерная плотность распределения вероятности и, следовательно, среднее значение и дисперсия случайного процесса не зависят от времени, а двумерная плотность распределения вероятности и корреляционная функция зависят только от разности временных аргументов.

В узком смысле под стационарным понимается процесс, ни одна статистическая характеристика которого не зависит от времени. В широком смысле условие стационарности требует независимости от времени первого и второго моментов. Все строго стационарные процессы – стационарны и в широком смысле, но не все процессы, стационарные в широком смысле, строго стационарны.

Рассмотрением именно этих процессов, для которых коэффициент корреляции является функцией временного сдвига , а не времени , мы и будем заниматься.

Таким образом, если стационарные случайные функции независимы, то функция корреляции между ними равна нулю. Функция взаимной корреляции для линейно связанных случайных функций равна произведению их среднеквадратичных значений, взятому с соответствующим знаком. Поэтому можно сказать, что корреляционная функция дает качественное

представление о линейной зависимости между значениями одной или двух

случайных функций в выбранные моменты времени (или в двух точках пространства).

Процессы, для которых среднее по совокупности реализаций совпадает со средним по времени при интервале усреднения , называются эргодическими.

Пусть получена запись случайного процесса . - интервал усреднения. Обозначим усреднение по времени волнистой чертой. По определению,

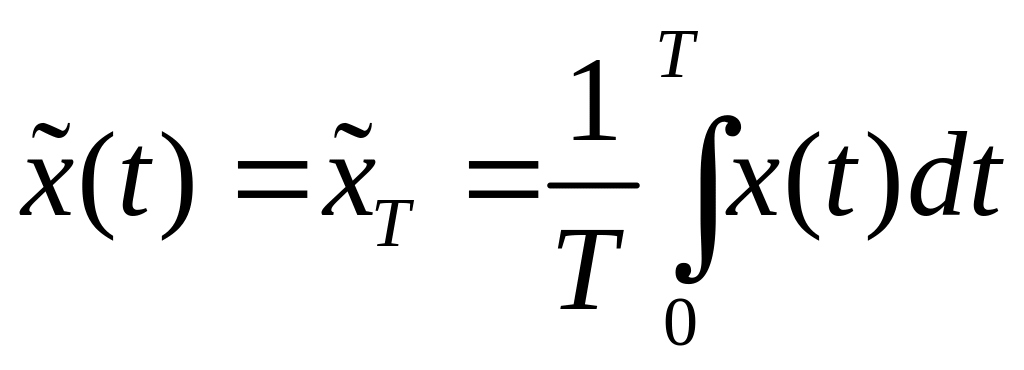. (68)

Если

, (69)

(здесь прямой чертой обозначено усреднение по совокупности реализаций), то процесс называется эргодическим.

Таким образом, для эргодического процесса усреднение по ансамблю может быть заменено усреднением во времени.

Найдем необходимое и достаточное условие эргодичности. Для этого после усреднения случайной величины х по времени усредним ее по совокупности:

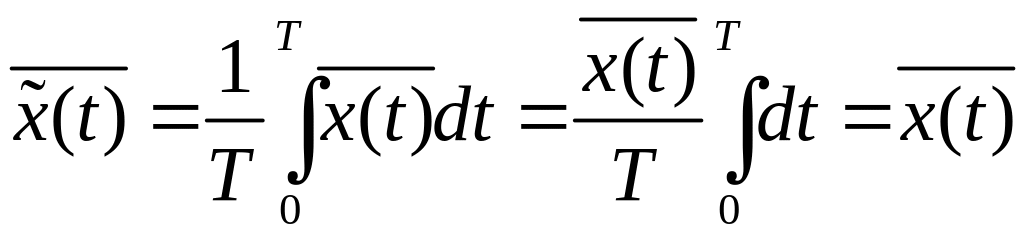. (70)

Если - стационарный процесс, .

Рассмотрим различие между средним по времени и средним по совокупности. Мерой этого различия является дисперсия .

Если при , мы имеем дело с эргодическим процессом.

Итак, выполнение равенства

(71)

служит необходимым и достаточным условием эргодичности процесса.

Поскольку мы берем функцию корреляции в виде , речь, здесь, следовательно, идет о стационарных процессах.

Эргодические процессы составляют подкласс стационарных процессов. Так что не все стационарные процессы эргодичны.

Строгая эргодичность означает, что множество реализаций данного случайного процесса на некотором конечном отрезке времени характеризуются теми же многомерными законами распределения любого порядка, что и множество отрезков этого процесса той же длительности, «нарезанных» из одной бесконечно длинной реализации.

Стационарный процесс будет эргодическим, если временное среднее и корреляционная функция будут одинаковыми для всех реализаций процесса. Для эргодичности гауссовского случайного процесса достаточно, чтобы он был стационарным, а его корреляционная функция удовлетворяла требованиям:

(72)

где

, (73)

а и - корреляционная функция и среднее значение процесса соответственно.

Чтобы охарактеризовать случайные процессы и , необходимо задать средние значения и , дисперсии и , а также корреляционные функции и . Если между процессами существует вероятностная связь, для описания степени этой связи вводят взаимные корреляционные функции. По определению, взаимные корреляционные функции представляют собой математическое ожидание произведения значений двух процессов, взятых в разные моменты времени:

. (74)

Вычисляются они по формулам:

, (75)

. (76)

Основные свойства взаимной корреляционной функции следующие:

1. В общем случае взаимные корреляционные функции не являются четными относительно . Тем не менее, существует вид симметрии, описываемый соотношением

. (77)

2. Взаимная корреляционная функция не обязательно должна иметь максимум при =0.

3. Если два процесса статистически независимы,

. (78)

Для комплексных случайных процессов особенность состоит в том, что при усреднении произведения значений процессов один из сомножителей берется комплексно сопряженным:

, (79)

, (80)

где звездочкой отмечены комплексно-сопряженные функции.

Для комплексных процессов соответственно

(81)

Спектральная плотность мощности и автокорреляция

Спектральная плотность мощности случайного процесса определяется выражением:

, (82)

где - интервал наблюдения случайного процесса, - непрерывный аналог коэффициентов Фурье отдельных реализаций усеченного случайного процесса , отличного от нуля на интервале наблюдения. Величина называется периодограммой для конкретной реализации .

Спектральная плотность мощности и корреляционная функция случайного процесса связаны между собой парой преобразований Фурье:

. (83)

Первое соотношение известно под названием формулы Винера –Хинчина. Спектральная плотность мощности обладает следующими свойствами:

1. – четная функция ;

2. – вещественная функция частоты ;

3. – неотрицательная функция частоты, то есть для любой частоты

.

Взаимная спектральная плотность для стационарных случайных процессов определяется в виде:

. (84)

. Свойства взаимной спектральной плотности:

1. Взаимные спектральные плотности являются комплексно сопряженными функциями ;

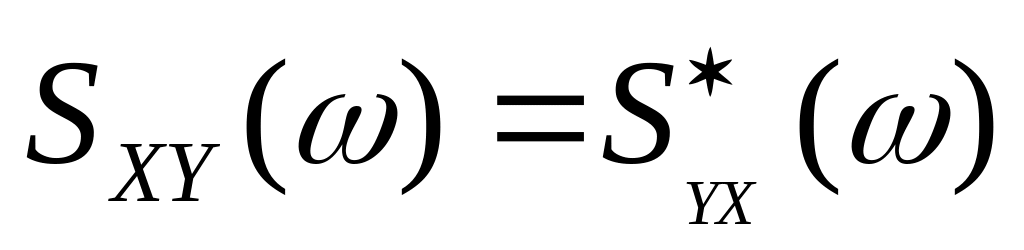2. и - четные функции частоты ;

3. и 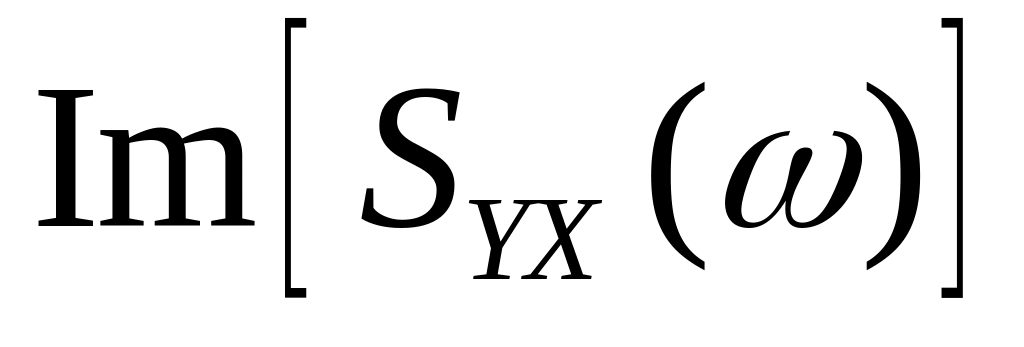- нечетные функции частоты .

Функция когерентности определяется как

(85)

и представляет собой своего рода «коэффициент корреляции» в частотной области.

Спектральная плотность суммы двух некоррелированных процессов равна сумме спектральных плотностей процессов, образующих сумму.

Белый шум – случайный процесс, имеющий постоянную спектральную плотность на всех частотах, бесконечную дисперсию и равный нулю интервал корреляции для всех значений , то есть .

Корреляционная функция белого шума имеет вид:

. (86)

Белый шум является моделью абсолютно случайного процесса, когда значения случайного процесса в любые два несовпадающих, но сколь угодно близких момента времени статистически независимы, а интегральная ширина энергетического спектра бесконечно велика. Он представляет собой физически нереализуемую математическую абстракцию. Однако многие процессы в рассматриваемом на практике интервале частот имеют спектр, очень близкий к равномерному. В этом случае их можно аппроксимировать белым шумом.

В случае постоянства спектральной плотности мощности случайного процесса введение такой идеализации позволяет разрабатывать достаточно легко применимые оптимальные методы фильтрации.

Квазибелым шумом называется случайный процесс, спектральная плотность которого постоянна в пределах ограниченной полосы частот и равна нулю вне ее:

. (87)

где - физическая частота спектра в герцах.

Говорят, что процесс, энергетический спектр которого непостоянен во всем частотном диапазоне, является окрашенным случайным процессом.

Корреляционная функция рассчитывается достаточно просто.