Формула Байеса

Формула Байеса связана с очень важной в настоящее время проблемой выделения сигналов на фоне шумов и касается так называемой «переоценки гипотез».

Пусть имеется ряд возможных исходов какой-либо операции. Обозначим их как события .

К примеру, это могут быть записи интенсивности сигнала на фоне шумов. Наличие сигнала обозначим через событие К.

Пусть предварительно известны вероятности реализаций . Пусть известны также условные вероятности события К при осуществлении события . Это так называемые априорные вероятности, известные нам до опыта. В результате опыта получена реализация, в которой событие К произошло. Как изменятся при этом вероятности различных исходов нашего опыта? То есть встает вопрос об определении апостериорных вероятностей.

Как следует из формулы условной вероятности (6),

(14)

Предстоит определить .

Очевидно,

. (15)

Здесь - полная вероятность события К. Понятие полной вероятности применяется в тех случаях, когда имеется неопределенность относительно причин, вызывающих следствие K. Для снятия этой неопределенности выдвигается ряд гипотез

Формула Байеса является отражением причинно-следственной связи в случайных явлениях. Она показывает, как надо изменить апостериорные вероятности по сравнению с априорными в связи с появлением события K.

Пример:

Имеется три совершенно одинаковых ящика. Пусть в одном находятся два белых шара, во втором - один белый и один чёрный, в третьем – два черных. Предположим, мы вытащили шар из одного из ящиков, и он оказался белым. Рассчитать вероятность того, что в ящике остался тоже белый шар.

Очевидно, априорная вероятность правильного выбора ящика . Вероятность того, что вытащим белый шар, будет различна для разных ящиков. Для того, в котором находятся два белых шара, она равна . Для ящика, в котором один из шаров – черный, эта вероятность равна . Для третьего ящика она равна нулю. Эти вероятности известны нам до опыта. Найдем апостериорные вероятности того, что мы взяли шар из ящика, где было:

1 – два белых шара:

;

2 – один белый и один черный шар:

.

Очевидно, что для третьего ящика искомая вероятность равна нулю:

.

Обобщая формулу полной вероятности и теорему Байеса (15) на случай непрерывно изменяющихся случайных величин – случайного процесса, - найдём, что условная плотность вероятности случайной величины при условии, что А имело место, дается формулой:

, (16)

где - вероятность события А при условии, что случайная величина приняла значение х; в дано случае - плотность вероятности случайной величины х до опыта (см. следующую лекцию).

Вероятность при n независимых испытаниях

Какова вероятность того, что при n независимых испытаниях произойдёт m благоприятных событий?

Пусть известна вероятность события при одном испытании. Очевидно, что вероятность того, что событие не происходит, равна

. (17)

Число неблагоприятных исходов будет .

Совместное осуществление двух независимых событий имеет вероятность

. (18)

Очевидно, что вероятность m событий при n испытаниях

(19)

Это выражение носит название закона Бернулли или биномиального распределения.

Пример: Радиолокатор посылает 8 импульсов в течение некоторого интервала времени. Для обнаружения цели необходимо принять не менее 5 отраженных от нее импульсов. Задана вероятность того, что отраженный сигнал потонет в шумах: Следовательно, вероятность поступления одного импульсов равна . Какова вероятность обнаружения?

Если из 8 импульсов будет принято 5, 6, 7 или все 8 импульсов, цель будет обнаружена.Следовательно, искомая вероятность равна

или

.

Пусть n очень велико. Как тогда изменится формула (19)?

.

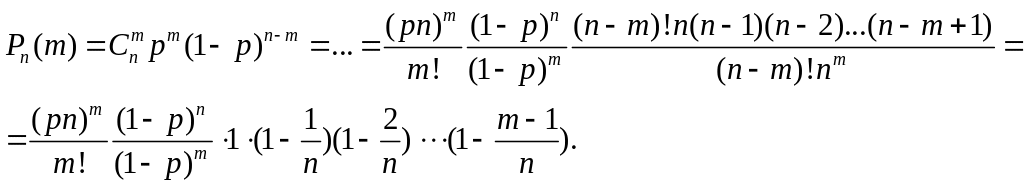Рассмотрим дискретные случайные величины. Поставим задачу следующим образом. На оси абсцисс случайным образом распределены точки. Выберем интервал длиной l и обозначим через вероятность того, что в интервал длиной l попадает ровно k точек. Распределение считается заданным, если для любого k известно . Набор вероятностей при k =0;1;2;…будет называться распределением Пуассона, если расположение точек на оси абсцисс удовлетворяет следующим условиям:

1. Условие стационарности. Оно означает, что вероятность попадания того или иного количества точек в интервал зависит от длины интервала, но не зависит от положения интервала на оси абсцисс. Иными словами, точки распределены на оси абсцисс с одинаковой средней плотностью. Обозначим ее через . Фактически это математическое ожидание числа точек, приходящихся на единицу длины.

2. Условие независимости, - события, состоящие в попадании того или иного числа точек в неперекрывающиеся отрезки, независимы.

3. Условие ординарности, - вероятность попадания в бесконечно малый интервал более одной точки есть бесконечно малая величина более высокого порядка малости по сравнению с вероятностью попадания в него ровно одной точки.

4. При выполнении этих условий требуется определить - вероятность того, что в интервал длиной l попадает ровно k точек. Ввиду достаточной простоты вывода запишем лишь конечный результат:

(20)

Это распределение вероятностей носит название распределения Пуассона.