ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Факультет систем управления

(дистанционная форма обучения)

Кафедра автоматизиции обработки информации (АОИ)

Контрольная работа № 1

по дисциплине “Спецглавы математики - 1”

автор учебного пособия: Смыслова З. А.

Специальность: 220200

Выполнил

“ __”_августа__ 2002 г.

Принял:

________________________________

(ФИО преподавателя)

__________________

(оценка)

“ _____”___________ 2002 г.

2002 г.

Вариант 7

1. Решить задачу, используя диаграмму Эйлера-Венна.

Каждый из студентов группы занимается хотя бы одним видом спорта. Пятеро занимаются альпинизмом, шестеро - волейболом, 10 человек - борьбой. Известно, что двое занимаются и альпинизмом, и волейболом; трое волейболом и борьбой; четверо - альпинизмом и борьбой; а один занимается всеми тремя видами спорта. Сколько студентов занимаются только борьбой?

Решение

В задаче идет речь о трех множествах В, Б, А - студентах занимающимися волейболом, борьбой и альпинизмом соответственно.

Используя обозначение n(X) - кол-во элементов множества X, запишем кратко условие задачи:

n(А) = 5; n(В) = 6; n(Б) = 10

n(АВ) = 2; n(ВБ) = 3; n(АБ) = 4; n(АВБ) = 1

В задаче требуется найти n(Б \ (АВ)), т.е. множество таких элементов Б которые не содержаться ни в множестве А ни в множестве В.

Перенесем данные задачи на диаграмму Эйлера-Венна. Разметку диаграммы начнем с множества АВБ - здесь один элемент. В множестве АВ - 2 элемента, но один из них уже учтен. Оставшийся 1 элемент проставляем на диаграмме и т. д.

А

В

1

2

1

3

2

4

Б

Теперь на диаграмме все элементы учтены по одному разу. Из диаграммы видно, что количество студентов занимающихся только борьбой равно 4.

Ответ: 4 студента.

2. Задано универсальное множество U={1, 2, 3, 4, 5, 6, 7, 8} и множества X = {2, 4, 5, 7, 8}, Y = {1, 2, 3, 4, 6}, Z = {4, 5, 6, 8}. Записать булеан множества X, любое разбиение множества Y, покрытие множества Z. Выполнить действия .

Решение

Для построения булеана множества X воспользуемся двоичной записью номера подмножества. Если множество X содержит n элементов, его булеан содержит подмножеств - в нашем случае 32 подмножества. Будем записывать номер подмножества пятиразрядным двоичным числом от 0 до 31, включая в подмножество только те элементы. которым соотвестсвует единица в двоичном разряде.

Булеан множества X

Номер подмножества	Двоичная запись номера	Подмножества множества X = {2, 4, 5, 7, 8}
0	00000	{} =
1	00001	{8}
2	00010	{7}
3	00011	{7, 8}
4	00100	{5}
5	00101	{5, 8}
6	00110	{5, 7}
7	00111	{5, 7, 8}
8	01000	{4}
9	01001	{4, 8}
10	01010	{4, 7}
11	01011	{4, 7, 8}
12	01100	{4, 5}
13	01101	{4, 5, 8}
14	01110	{4, 5, 7}
15	01111	{4, 5, 7, 8}
16	10000	{2}
17	10001	{2, 8}
18	10010	{2, 7}
19	10011	{2, 7, 8}
20	10100	{2, 5}
21	10101	{2, 5, 8}
22	10110	{2, 5, 7}
23	10111	{2, 5, 7, 8}
24	11000	{2, 4}
25	11001	{2, 4, 8}
26	11010	{2, 4, 7}
27	11011	{2, 4, 7, 8}
28	11100	{2, 4, 5}
29	11101	{2, 4, 5, 8}
30	11110	{2, 4, 5, 7}
31	11111	{2, 4, 5, 7, 8}

Итак, B(X) = { , {8}, {7}, {7, 8}, {5}, {5, 8}, {5, 7}, {5, 7, 8}, {4}, {4, 8}, {4, 7}, {4, 7, 8}, {4, 5}, {4, 5, 8}, {4, 5, 7}, {4, 5, 7, 8}, {2}, {2, 8}, {2, 7}, {2, 7, 8}, {2, 5}, {2, 5, 8}, {2, 5, 7}, {2, 5, 7, 8}, {2, 4}, {2, 4, 8}, {2, 4, 7}, {2, 4, 7, 8}, {2, 4, 5}, {2, 4, 5, 8}, {2, 4, 5, 7}, {2, 4, 5, 7, 8}}.

Для множества Y построим разбиение, состоящее из трех блоков R(Y) = {Y1, Y2, Y3}, например, таким образом:

Y1 = {1, 2}, Y2 = {3, 4}, Y3 = {6}

Определение разбиения выполняется: множества Y1, Y2, Y3 не пусты, не пересекаются (Y1Y2=, Y2Y3=, Y1Y3=), их объединение равно множеству Y:

Y1Y2Y3 = (Y1Y2)Y3 = ({1, 2}{3, 4}){6} = {1, 2, 3, 4}{6} = {1, 2, 3, 4, 6}.

Для построения покрытия выберем подмножества Z1 = {4, 5} и Z2={5, 6, 8}.

Полученная система множеств P(Z) = {Z1, Z2} состоит из двух блоков, объединение которых равно множеству Z:

Z1Z2 = {4, 5}{5, 6, 8} = {4, 5, 6, 8} = Z.

Для выполнения действия найдем:

= (U \ X) = ({1, 2, 3, 4, 5, 6, 7, 8} \ {2, 4, 5, 7, 8}) = {1, 3, 6}

ZY = {4, 5, 6, 8}{1, 2, 3, 4, 6} = {4, 6}

Таким образом, = {1, 3, 6} \ {4, 6} = {1, 3}.

3. Упростить, используя законы и тождества алгебры множеств

(перечислить используемые законы).

A(B)B(BC)B .

Решение

Расставим скобки соответственно приоритетам операций и определим порядок действий:

Выполним преобразования, указывая номер закона над знаком равенства:

1)

2)

3)

4)

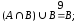
Ответ: A(B)B(BC)B = B .

4. Пользуясь только определениями операций над множества и определением равенства множеств, доказать

A(B) = AB .

Доказательство

Пусть X = A(B); Y = AB .

Покажем, что согласно определению равенства множеств XY и YX.

Пусть x - произвольный элемент множества X. Тогда по определению пересечения множеств (xA и x(B)). Далее по определению объединения множеств (xA и (x или xB)).

Следовательно, ((xA и x) или (xA и xB))

=> (x или (xA и xB)) => (xA и xB) => x(AB) = Y.

Таким образом, для любого xX выполняется xY, т.е. XY.

Докажем теперь, что YX.

Пусть y - произвольный элемент множества Y. Тогда

(yY) => (yA и yB) => (y или (yA и yB)) =>

((yA и y) или (yA и yB)) => (yA и (y или yB))

=> y A(B) = X. Так как элемент y выбран произвольно, то YX.

Таким образом, XY и YX, следовательно X=Y .

5. Пусть X={0, 1, 2, 3, 4}. Бинарное отношение RXX задано характеристическим свойством:

R = {(a, b)| a+b делится на 3, a, b X}.

Представить отношение R другими возможными способами. Какими свойствами обладает это отношение? Является ли оно отношением эквивалентности?

Решение

Отношение R можно задать перечислением всех элементов:

R = {(0, 0), (3, 3), (0, 3), (3, 0), (1, 2), (2, 1), (2, 4), (4, 2)}

Наглядно представить отношение R можно с помощью графика (рис.1), схемы (рис.2), графа (рис.3), матрицы отношения (рис.4).

DR

DR

ER

4

*

4

4

3

*

*

3

3

2

*

*

2

2

1

*

1

1

*

*

0

0

ER

1

4

3

2

0

Рис. 1

Рис. 2

1

2

0

3

4

Рис. 3

Рис. 4

Выясним, какими свойствами обладает отношение. Отношение не является ни рефлексивным, ни антирефлексивным. Действительно, при a=b, условие “a+b делится на 3” принимает вид a + a = 2a - делится на 3 не выполняется при любых значениях aX, с другой стороны существуют значения a для которых это условие выполняется. Так например, для a=1 это условие не выполняется (21 = 2 - не делится на 3), а для a=3 - выполняется (23 = 6 - делится на 3). Таким образом, мы выяснили, что отношение не является ни рефлексивным, ни антирефлексивным.

Проверим, является ли отношение симметричным. Пусть a+b делится на 3 (т.е. (a, b)R). Составим пару (b, a) и для нее проверим характеристическое свойство отношения:

b + a = a + b.

Очевидно, что a + b делится на 3 (по условию), следовательно b + a делится на 3, т.е. (b, a)R. Отношение симметрично.

Проверим, является ли отношение транзитивным.

Пусть (a, b)R и (b, c)R, т.е. a + b делится на 3 и b + c делится на 3.

Будет ли делится на 3 выражение a + c, т.е. будет ли (a, c)R?

Преобразуем a + c = a + c + b - b = (a+b) - (b+c) + 2c. Первые два слагаемые делятся на 3 по условию, а третье слагаемое 2c не делится на 3 (в общем случае). Следовательно, отношение не является транзитивным.

Очевидно, что поскольку данное отношение не является одновременно рефлексивным, симметричным и транзитивным, то оно не является отношением эквивалентности.

6. Дано множество X = {1, 3, 6, 9} и отношение R = {(x, y)| x,yX, x - делитель y}. Показать, что отношение R является отношением порядка. Построить диаграмму Хассе частично упорядоченного множества (X, R). Существует ли в множестве X наибольший и наименьший элементы? Существуют ли несравнимые элементы?

Решение

Покажем, что отношение R рефлексивно, антисимметрично и транзитивно.

Рефлексивность имеет место, так как любое число является своим делителем, т.е. xX =>(x, x)R.

Пусть одновременно выполняются условия: (x, y) R и (y, x) R. Тогда x = y. Действительно, (x, y) R означает, что x - делитель y, т.е. mZ | y=mx. Одновременно nZ | x=ny.

Отсюда y= mny и mn = 1.

Последнее равенство выполняется при m = n = 1 (случай m = n = -1 исключается, т.к. все элементы множества X - положительные числа), т.е. x = y, и отношение R антисимметрично.

Пусть (x, y) R и (y, z) R, значит, найдутся m, k Z такие, что y = mx, z = ky. Тогда z = k (mx) = (k m)x = n x, где n = mkZ. Следовательно, x является делителем z и (x, z) R. Отношение R транзитивно.

Отношение R рефлексивно, антисимметрично и транзитивно, т.е. является отношением порядка.

Построим диаграмму Хассе частично упорядоченного множества (X, R). На нижнем (первом) уровне диаграммы поместим элемент xX, не имеющий других делителей кроме себя (x = 1). На втором уровне - элемент не имеющий других делителей кроме себя и элементов нижнего уровня (x = 3). Оставшиеся два элемента x = 6 и x = 9 делятся на себя и на все элементы втрого и первого уровней - помещаем их на третий уровень. Соединяем отрезком элементы соседних уровней, если элемент нижнего уровня является делителем элемента соседнего верхнего уровня. Диаграмма Хассе построена (рис.5). Пара элементов (x, y) R тогда и только тогда, когда двигаясь по диаграмме только вверх, мы можем пройти от элемента x до элемента y.

9

6

3

1

Рис. 5

По диаграмме Хассе легко обнаружить несравнимые элементы 6 и 9. Наибольшего элемента нет. А максимальных элементов два x = 6 и x = 9, т.к. в множестве нет элементов y таких, что “6 является делителем y” и “9 является делителем y”. В частично упорядоченном множестве (X, R) элемент x = 1 является делителем любого элемента множества и следовательно является наименьшим элементом.

7. Заданы отношения:

R: S:

A1	A2	A3		B1	B2	B3
a	e	d		a	b	c
a	b	c		b	e	d
d	a	b		d	e	d

Записать обозначения операций реляционной алгебры и выполнить их:

а) селекция отношения R по условию “A1 >A2”;

б) проекция на список (2, 3) объединения отношений R и S.

Решение:

Обозначение операции селекции . Чтобы выполнить эту опеацию вычеркиваем из отношения R все записи не удовлетворяющие условию “A1>A2” (знак “>” означает лексикографический (алфавитный) порядок):

A1	A2	A3
d	a	b

Объединение RS дает множество записей, которые принадлежат хотя бы одному из отношений R или S (данная операция возможна поскольку R и S - совместимы, т.е. их степени равны, а данные однотипны).

RS

C1	C2	C3
a	e	d
a	b	c
d	a	b
b	e	d
d	e	d

Обозначение проекции (RS). Чтобы выполнить эту операцию, выписываем второе и третье поле всех записей RS в новую таблицу (вычеркнули столбец C3), вычеркиваем две последние повторяющиеся строки.

(RS)

D1	D2
e	d
b	c
a	b

8. Даны множества A = {0, 2, 4} и B = {4n| nN}. Какова мощность множеств AB, AB, AB ?