17

Томский государственный университет

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Факультет систем управления

(дистанционная форма обучения)

Кафедра автоматизиции обработки информации (АОИ)

Контрольная работа № 1

по дисциплине “Спецглавы математики - 2”

автор учебного пособия: Пермякова Н. В.

Специальность: 220200

Выполнил

“ __”_августа__ 2002 г.

Принял:

________________________________

(ФИО преподавателя)

__________________

(оценка)

“ _____”___________ 2002 г.

2002 г.

Вариант 7

G0

G1

G2

Задание

1. Представьте графы G0 и G1 различными способами (по четыре для каждого графа).

Пронумеруем произвольно вершины и ребра графа G0:

IV

I

II

III

V

В графе G0 4 вершины и 4 ребра, следовательно матрица смежности графа G0 - матрица A(4x4), матрица инцидентности - B(4x5):

A(G0) = B(G0) =

Построим структуру смежности для орграфа G0. Это 4 связных списка:

• вершине 1 смежны вершины 1 и 2 - 1: 2, 3;

• вершине 2 смежны вершины 1 и 3 - 2: 1, 3;

• у вершины 3 нет смежных вершин - 3: ;

• вершине 4 смежна вершина 4 - 4: 4;

Построим список ребер для орграфа G0. Размерность массивов начальных и конечных вершин равна m = 5.

NR = {1, 1, 2, 2, 4};

KR = {1, 2, 1, 3, 4}.

Пронумеруем произвольно вершины и ребра графа G1:

I

II

III

V

VI

IV

VII

В графе G1 6 вершин и 7 ребер, следовательно матрица смежности графа G1 - матрица A(6x6), матрица инцидентности - B(6x7):

A(G1) = B(G1) =

Построим структуру смежности для неорграфа G1. Это 6 связных списков:

• вершине 1 смежны вершины 4 и 5 - 1: 4, 5;

• вершине 2 смежны вершины 4 и 6 - 2: 4, 6;

• вершине 3 смежны вершины 4, 5, 6 - 3: 4, 5, 6;

• вершине 4 смежны вершины 1, 2, 3 - 4: 1, 2, 3;

• вершине 5 смежны вершины 1 и 3 - 5: 1, 3;

• вершине 6 смежны вершины 2 и 3 - 6: 2, 3;

Построим список ребер для орграфа G1. Так как в неорграфах одна вершина может быть и началом и концом ребра, то размерность массивов начальных и конечных вершин в списке ребер равна

2m = 27=14.

NR = {2, 2, 3, 3, 3, 1, 1, 6, 4, 6, 5, 4, 4, 5};

KR = {6, 4, 6, 5, 4, 4, 5, 2, 2, 3, 3, 3, 1, 1}.

1. Запишите алгоритм (или составьте программу) нахождения вершины графа, имеющей нулевую полустепень захода. Граф задан матрицей инцидентности.

По определению, число дуг орграфа для которых вершина x является концом называется полустепенью захода вершины x и обозначается .

По свойству матрицы инцидентности число элементов i-ой строки матрицы равных -1 равно полустепени захода i-ой вершины.

Таким образом, для вершины имеющей нулевую полустепень захода в соответствующей строке матрицы инцидентности не должно быть ни одного элемента равного -1.

Исходя из вышесказанного составим алгоритм решения данной задачи.

Обозначения, использованные в алгоритме:

m - количество вершин графа, n - количество ребер графа,

A - матрица инцидентности

НАЧАЛО

Ввод A; {Ввод матрицы инцидентности}

{Цикл по матрице}

i:=1; j:=1;

ЦИКЛ_ПОКА (i  m и j  n) {цикл по строкам}

j:=1;

ЦИКЛ_ПОКА (j  n и A[i, j]  -1) {цикл по столбцам}

j:= j +1;

ВСЕ_ЦИКЛ

ЕСЛИ j > n, ТО Печать i; {если в i-ой строке матрицы нет

ни одного элемента равного -1, то напечатать номер i

вершины имеющей нулевую полустепень захода}

i:=i +1;

ВСЕ_ЦИКЛ

КОНЕЦ

2. Изоморфны ли графы G1 и G2 ?

Занумеруем произвольным образом вершины графов G1 и G2:

G1

G2

Для того, чтобы два графа G1(X1, V1) и G2(X2, V2) были изоморфны, необходимо, чтобы выполнялись равенства | X1| =| X2|, | V1|=| V2|. Проверим выполнение этих условий для графов G1 и G2 :

| X1| = 6 | X2| = 6

| V1| = 7 | V2| = 7

Далее сравним степени вершин в графах G1 и G2.

Граф G1: 1(1) = 2, 1(2) = 2, 1(3) = 3, 1(4) = 3, 1(5) = 2, 1(6) = 2.

Граф G2: 2(1) = 2, 2(2) = 2, 2(3) = 3, 2(4) = 3, 2(5) = 2, 2(6) = 2.

У обоих графов одинаковое количество вершин со степенью 2 и одинаковое количество вершин со степенью 3.

Построим соответствие f: G1 G2 следующим образом:

f(1) = 6, f(2) = 2, f(3) = 4, f(4) = 3, f(5) =5 , f(6) = 1.

Проверим сохраняет ли построенная биекция смежность.

Вершина 1 смежна вершине 4 и f(1) = 6 смежна f(4) = 3.

Вершина 1 смежна вершине 5 и f(1) = 6 смежна f(5) = 5.

Вершина 2 смежна вершине 4 и f(2) = 2 смежна f(4) = 3.

Вершина 2 смежна вершине 6 и f(2) = 2 смежна f(6) = 1.

Вершина 3 смежна вершине 4 и f(3) = 4 смежна f(4) = 3.

Вершина 3 смежна вершине 5 и f(3) = 4 смежна f(5) = 5.

Вершина 3 смежна вершине 6 и f(3) = 4 смежна f(6) = 1.

Вершина 4 смежна вершине 1 и f(4) = 3 смежна f(1) = 6.

Вершина 4 смежна вершине 2 и f(4) = 3 смежна f(2) = 2.

Вершина 4 смежна вершине 3 и f(4) = 3 смежна f(3) = 4.

Вершина 5 смежна вершине 1 и f(5) = 5 смежна f(1) = 6.

Вершина 5 смежна вершине 3 и f(5) = 5 смежна f(3) = 4.

Вершина 6 смежна вершине 2 и f(6) = 1 смежна f(2) = 2.

Вершина 6 смежна вершине 3 и f(6) = 1 смежна f(3) = 4.

Установленное соответствие является биекцией, сохраняющей смежность. Следовательно, графы G1 и G2 изоморфны.

3. Запишите бинарное отношение, заданное графом G0. Какими свойствами оно обладает?

Пронумеруем вершины графа произвольным образом.

Запишем бинарное отношение представленное графом G0 перечислением, считая, что элементы множества X - вершины графа, тогда элментами бинарного отношения Gb будут дуги орграфа

Gb = {(1, 1), (4, 4), (1, 2), (2, 1), (2, 3)}

Отношение Gb не обладает свойством рефлексивности, т.к. не выполняется условие (x, x)  R,  xX. Пары (2, 2) и (3, 3)  G0. Не у всех вершин графа есть петли.

Отношение Gb не обладает свойством антирефлексивности, т.к. не

выполняется условие (x, x)  R,  xX. Пары (1, 1) и (4, 4)  G0. Свойство антирефлексивности предполагает отсутствие петель в графе.

Отношение Gb не обладает свойством симметричности, т.к. не

выполняется условие xRy yRx,  x,yX.

В графе G0 есть пара (2, 3), но нет пары (3, 2).

Отношение Gb не обладает свойством антисимметричности, т.к. не

выполняется условие (x, y)  R и (y, x)  R  x=y,  x,yX.

В графе G0 есть дуга (1, 2) и (2, 1), но 21.

Отношение Gb не обладает свойством несимметричности, т.к. не

выполняется условие (x, y)  R  (y, x) R,  x,yX, потому что в графе G0 есть дуга и (1, 2) и дуга (2, 1).

Отношение Gb не обладает свойством транзитивности, т.к. не

выполняется условие (x, y)  R и (y, z)  R  (x, z) R,  x,y,zX.

Например, в графе G0 есть дуга (1, 2) и дуга (2, 3), но нет транзитивно замыкающей дуги (1, 3).

4. Является ли граф G1 планарным? Если да, то изобразите изоморфный ему плоский граф.

Занумеруем произвольным образом вершины графа G1:

G1

По критерию Понтрягина-Куратовского граф не планарный, если в нем можно выделить подграф K5 или K3,3. Очевидно, что не является графом вида K3,3. Проверим можно ли выделить в графе G1 подграф K5.

Рассмотрим все возможные подграфы графа G1, множество вершин которых состоит из пяти элементов.

Для этого из графа G1 поочередно удаляется по одной вершине, всего можно рассмотреть шесть таких подграфов:

Ни один из построенных подграфов не является K5. Таким образом, граф G1 - планарный граф. Изоморфный ему плоский граф имеет вид:

5. Запишите матрицы достижимости и взаимодостижимости для графа G0. Выделите сильные компоненты графа.

Пронумеруем вершины графа произвольным образом.

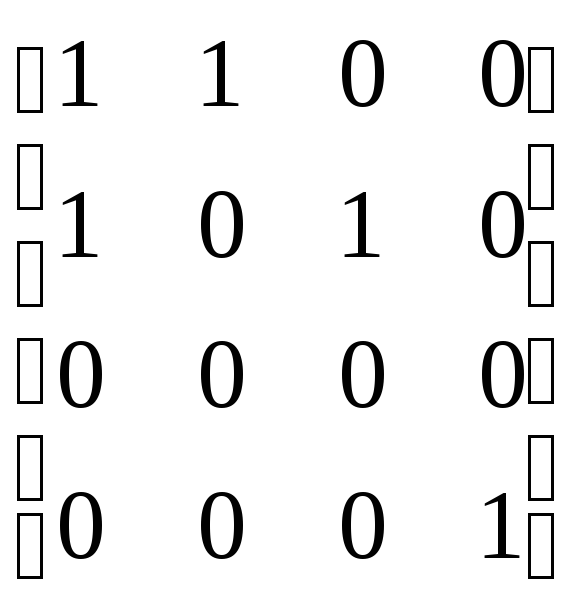
Построение матрицы достижимости R. Размер матрицы (4x4).

Из вершины 1 можно попасть в вершины 1, 2 и 3. Элементы первой строки матрицы кроме четвертого равны 1.

Из вершины 2 можно попасть в вершины 1, 2, 3 (вершина 2 достижима сама для себя по определению). Следовательно, все элементы второй строки кроме четвертого равны 1.

Вершина 3 достижима только сама для себя, поэтому в третьей строке только третий элемент равен 1, остальные равны 0.

Вершина 4 достижима только сама для себя, поэтому в четвертой строке только четвертый элемент равен 1, остальные равны 0.

Матрица достижимости R построена:

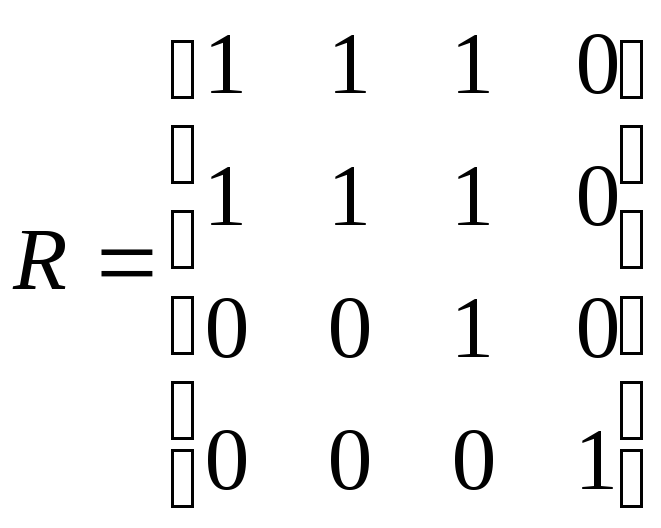
Для того, чтобы построить матрицу взаимодостижимости, построим матрицу контрдостижимости P. Матрица контрдостижимости равна транспонированной матрице достижимости.

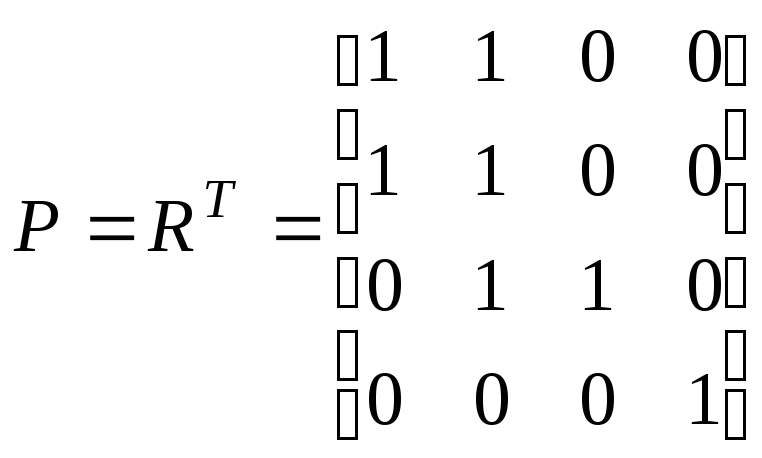
Элементы матрицы взаимодостижимости вычисляются по формуле:

Выделим сильные компоненты графа G0 по матрице взаимодостижимости.

Вычеркнем те столбцы и строки из матрицы S, которые соответствуют единичным элементам первой строки матрицы.

Это элементы с номерами j=1 и j=2. Вычеркнем столбцы 1, 2 и строки 1, 2. Таким образом, сильная компонента связности - подграф на вершинах 1, 2.

Далее рассмотрим измененную матрицу S.

Вычеркнем те столбцы и строки из матрицы , которые соответствуют единичным элементам первой строки матрицы.

Это элемент с номером j=3. Вычеркнем столбец 3 и строку 3. Следующая сильная компонента связности подграф на вершине 3.

После этого в измененной матрице остался один элемент, это третья сильная компонента графа G0 - граф с одной вершиной 4.

3