III. Табличный способ задания функции

Пусть дана таблица

x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7
y	−1	0	1	2	3	4	5	6

Поставим в соответствие каждому значению , записанному в первой строке таблицы, число , стоящее во второй строке под числом . Тогда, можно сказать, что функция задана таблично. Областью определения этой функции является множество, состоящее из 8 чисел . Они перечислены в первой строке таблицы. Множеством значений этой функции является множества, состоящее из 8 чисел , перечисленных во второй строке. С помощью таблицы можно задать функцию только при конечном числе значений аргумента. Таблицы часто используются для задания функции.

Пример: Таблицы тригонометрических функций; таблицы логарифмов и т.д.

IV. Графический способ задания функции

Соответствие между переменными и y задается посредством графика. Обычно графики чертятся с помощью самопишущих приборов. Данный способ задания функции используется при физических, медицинских измерениях.

Классификация функций по их свойствам

I. Основные простейшие функции:

1) постоянная , где .

2) степенная , где .

3) показательная .

4) логарифмическая .

5) тригонометрическая , .

6. обратные тригонометрические

.

I. Элементарные функции

Определение №1. Всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций и конечное число суперпозиций основных простейших функций, называется элементарной функцией.

Элементарные функции обычно делятся на классы:

1. Многочлены (полиномы).

К ним относятся функции, которые могут быть заданы формулами вида:

Если , то число называется степенью данного многочлена.

Многочлены называются целой рациональной функцией.

Определение №2. Многочлены первой степени называются линейными функциями .

2. Дробно-рациональные функции.

К этому классу функций относятся функции, которые могут быть заданы в виде: , где и - многочлены степеней и

.

Определение №3. Функция, представляющая собой отношение двух целых рациональных функций называется дробно-рациональной функцией.

Определение №4. Совокупность целых рациональных и дробно-рациональ­ных функций образует класс рациональных функций.

3. Иррациональные функции.

Определение №5. Иррациональной функцией называется функция, которая может быть задана с помощью суперпозиций конечного числа рациональных функций, степенных функций с рациональными показателями и четырех арифметических операций.

Пример: .

4. Трансцендентные функции.

Определение №6. Всякая функция не являющаяся рациональной и иррацио­нальной называется трансцендентной функцией.

Пример: ; и т.д.

Четные и нечетные функции

Определение №1. Симметричный промежуток – это промежуток, сим­метричный относительно начала координат ( ; ; ).

Определение №2. Функция , заданная на симметричном проме-жутке называется четной, если для любых значений из области опреде-ления справедливо равенство .

Примеры: а) ; б) ; в) .

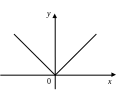
а) б) в)

Как видно из определения и приведенных примеров, графики всех четных функций симметричны относительно оси координат.

Определение №3. Функция , заданная на симметричном промежутке называется нечетной, если для любых значений из ее области определения справедливо равенство .

Примеры: а) ; б) ; в) .

а) б) в)

Особенностью нечетных функций является то, что их графики симметричны относительно начала координат.