Лабораторная работа № 6. Обработка и представление результатов прямых измерений при наличии группы однородных и равнорассеянных многократных наблюдений

Цель работы: рассмотреть методику обработки и представления результатов прямых из­мерений для двух групп наблюдений.

Краткие теоретические сведения

Одним из условий правомерности статистической обработки результатов многократных наблюдений является требование однородности выборки, т. е. принадлежности всех членов выборки к одной и той же генеральной совокупности.

На практике нередко одну и ту же величину измеряют несколькими сериями, сделанными в различное время и по новому настроенной измеритель­ной аппаратуры. Также от серии к серии могут меняться параметры внешней среды, приборы, исследователи и т. д. Такие измерения называют неравноточнымииями. В этом случае мы получаем k групп по n_j (j = 1,2,..., m) результатов наблюдений в каждой.

Для повышения точности их желательно объединить в один ряд и обрабатывать по типовым правилам, учитывая, что общее количество результатов наблю­дений в этом объединенном ряду окажется равным сумме количеств результатов наблюдений в каждой группе. Однако такое объединение правомерно, если группы результатов наблюдений являются однородными и равнорассеянными.

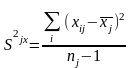Группы наблюдений называются однородными и равнорассеяннымй, если оценки среднего арифметического и оценки дисперсии для ряда наблюдений, соответственно

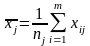
во всех группах статистически одинаковы.

Проверка равнорассеянности и однородности групп наблюдений

Равнорассеянность и однородность групп наблюдений проверяется методами математической статистики, известными под общим названием дисперсионного анализа.

Дисперсии не подчиняются нормальному распределению, для них не подходит t-критерий. Для сравнения дисперсий используется критерий Фишера (F –распределение) или критерий Бартлетта.

Критерий Фишера. Если при вы­бранном уровне значимости q (уровень значимости при проверке гипотезы, вы­бирается обычно равным 0,05) окажется, что:

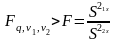
(6.1)

г де , а ν₁ = n₁ ̶ 1 и ν₂ = n₂ ̶ 1 - число степеней свободы для первой и второй дисперсии соответственно, то дисперсии считаются статистически неразличимы­ми, т. е. являются независимыми оценками одной и той же дисперсии. В противном случае гипотезу о равенстве выборочных дисперсий отвергают. Значе­ния распределения Фишера приведены в приложении.

Гипотезу о равнорассеянности и однородности результатов наблюдений прове­ряют в два этапа.

1. Вначале проверяется гипотеза о равенстве оценок дисперсий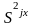 во всех группах наблюдений. Для этого их располагают в вариационный ряд в порядке возрастания и проверяют значимость отношения

. Если это соотношение незначимо, то незначимы и все остальные. Тогда гипотеза о том, что рассея­ние результатов наблюдений относительно средних значений во всех группах статистически одинаково, принимается. В противном случае признается, что дисперсии и 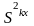статистически отличны друг от друга, и проверяется значи­мость отношений других дисперсий из вариационного ряда. В данном случае мы ограничимся случаем двух групп наблюдений, когда достаточно использовать формулу (6.1).

2. При равенстве оценок дисперсий в группах проверяется гипотеза об однородности, т. е. о равенстве в них математических ожиданий. Эта гипотеза может быть прове­рена несколькими методами. В частности, при нормальном распределении ре­зультатов наблюдений равенство двух математических ожиданий можно прове­рять с помощью критерия Стьюдента.

В этом случае вычисляется величина:

(6.2)

Если при выбранном уровне доверительной вероятности Р_д (доверительная вероятность при проверке гипотезы выбирается обычно равной 95%) окажется, что |t_1-2| < t_v, где t_v выбирается по таблице t - распределения Стьюдента при числе степеней свободы, равном ν = n₁+n₂ - 2, то гипотеза о равенстве математических ожиданий принимается (следует иметь в виду, что число степеней ν свободы связано с чис­лом n, входящим в таблицу, соотношением v = n - 1).

Если имеется более двух групп результатов наблюдений, причем часть из них однородные и равнорассеянные, а часть нет, то совместную обработку проводят только для первой части результатов наблюдений. Методы обработки неоднород­ных и/или неравнорассеянных результатов в данной работе не рассматриваются.

По результатам проверки могут возникнуть следующие варианты:

1. группы однородны, т. е. незначительно различие средних при одинаковых рассеивании группы;

2. группы равнорассеяны, но различие средних незначительно;

3. группы равнорассеяны, но различие средних значительно;

4. группы неравнорассеяны и различие средних значительно.

По вариантам пп. 1 и 2 для повышения точности результата измерения можно объединить все группы в одну и вычислить по ней общий результат измерения. По вариантам пп. 3 и 4 объединять группы нецелесообразно, а следует выяснять причину расхождения между ними.