Содержание

Предисловие 3

1. Введение в математический анализ 4

2. Дифференциальное исчисление функции одной переменной 8

3. Дифференциальное исчисление функции многих переменных 13

4. Обыкновенные дифференциальные уравнения 26

Предисловие

Учебно-практическое пособие «Задачи и упражнения по экономике и управлению в базовых математических дисциплинах» составлено как приложение к учебнику В.В. Лебедева «Математика в экономике и управлении» - М.: НВТ - Дизайн, 2004.

Пособие включает четыре темы из программ учебных дисциплин «Математика» (высшая математика) и «Математический анализ»: введение в математический анализ, дифференциальное исчисление функции одной переменной, дифференциальное исчисление функции нескольких переменных, обыкновенные дифференциальные уравнения. По каждой теме приведено подробное решение базовых экономических задач и предлагается 10 аналогичных задач для самостоятельного решения.

Содержание задач предполагает, что студенты обладают базовыми знаниями по высшей математике и экономике.

Пособие рекомендуется для подготовки бакалавров по направлениям:

«Менеджмент» 080200, «Прикладная информатика» 230700, «Управление персоналом» 080400, «Экономика» 080100, "Экология и природопользование" – 022000, "Социология" – 040100, «Бизнес-информатика» - 080500.

Пособие может быть использовано студентами всех экономических направлений подготовки и различных форм обучения для самостоятельной работы.

1. Введение в математический анализ

Пример 1. Спрос на некоторый товар при цене  руб. за единицу товара составляет единиц товара, а при цене  руб. за единицу товара спрос составляет единиц товара.

Предполагая, что спрос линейно зависит от цены, вывести уравнение функции спроса и определить спрос при цене руб. за единицу товара.

Решение.

1 способ. Линейная зависимость спроса от цены определяется соотношением , где – некоторые константы. Для нахождения констант и подставим в уравнение данные задачи. Получаем систему двух линейных уравнений:

.

Откуда получаем функцию спроса .

Определим спрос при цене  руб. за единицу товара:  ед.

2 способ. Для нахождения линейной функции спроса можно использовать уравнение прямой, проходящей через две точки:

.

Ответ: ;  ед.

Задача 1. Спрос на некоторый товар при цене руб. за единицу товара составляет единиц товара, а при цене руб. за единицу товара спрос составляет единицам товара.

Предполагая, что спрос линейно зависит от цены, вывести уравнение функции спроса и определить спрос при цене р₃ руб. за единицу товара, если:

1.1. ;

1.2. ;

1.3. ;

1.4. ;

1.5. ;

1.6. ;

1.7. ;

1.8. ;

1.9. ;

1.10. .

Пример 2. Функция полных издержек некоторой фирмы задана уравнением (ден. ед.), где объем производства (единиц продукции). При этом цена производимой продукции на рынке равна 4 ден. ед. за единицу продукции.

Найти точку безубыточности фирмы.

Решение. Функция прибыли фирмы определяется как разность между доходом (выручкой от продаж) и издержками , т.е. задается уравнением . Точка безубыточности фирмы находится из условия

,

откуда следует .

Ответ:  ед.

Задача 2. Найти точку безубыточности однопродуктовой фирмы, если заданы функция полных издержек фирмы и цена производимой продукции на рынке :

2.1. ; ;	2.6. ; ;
2.2. ; ;	2.7. ; ;
2.3. ; ;	2.8. ; ;
2.4. ; ;	2.9. ; ;
2.5. ; ;	2.10. ; .

Пример 3. Заданы функции спроса и предложения на некоторый вид продукции, где – цена за единицу продукции.

При какой цене (значении ) наступает равновесие спроса и предложения, если ?

Решение. Точка равновесия – точка пересечения графиков функций спроса и предложения . графики данных функций спроса и предложения – отрезки прямых в первой четверти. Для нахождения точки равновесия надо приравнять «спрос» и «предложение»: . Откуда  ден. ед. Обратите внимание, что спрос превышает предложение для .

Ответ:  ден. ед.

Задача 3. Найти точку равновесия, если известны функции спроса и предложения на некоторый вид продукции (решение проиллюстрировать графиками в плоскости ):

3.1. ;

3.2. ;

3.3. ;

3.4. ;

3.5. ;

3.6. ;

3.7. ;

3.8. ;

3.9. ;

3.10. .

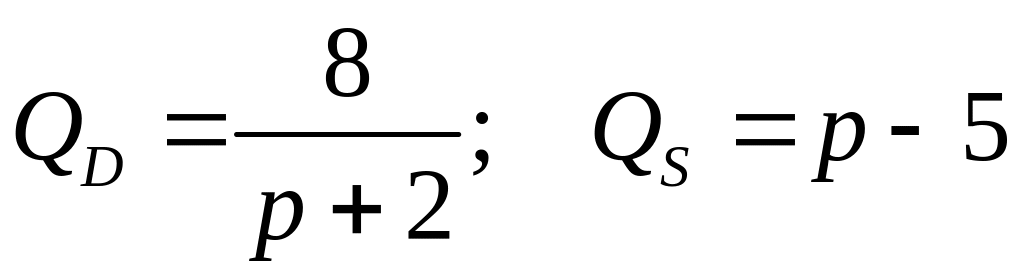Пример 4. Построить бюджетное множество, которое отражает покупательные возможности потребителя двух товаров, если на приобретение этих товаров расходуется не более ден. ед. Известно, что цены товаров равны  ден. ед. и  ден. ед. соответственно.

Решение. Если первый товар покупается в количестве единиц, а второй  в количестве единиц, то за покупку будет заплачено  ден. ед., и эта сумма не может превышать  ден. ед., а значит .

Бюджетное множество задается системой неравенств:

или

и представляет собой на плоскости треугольник ОАВ. Точки пересечения с осями имеют координаты 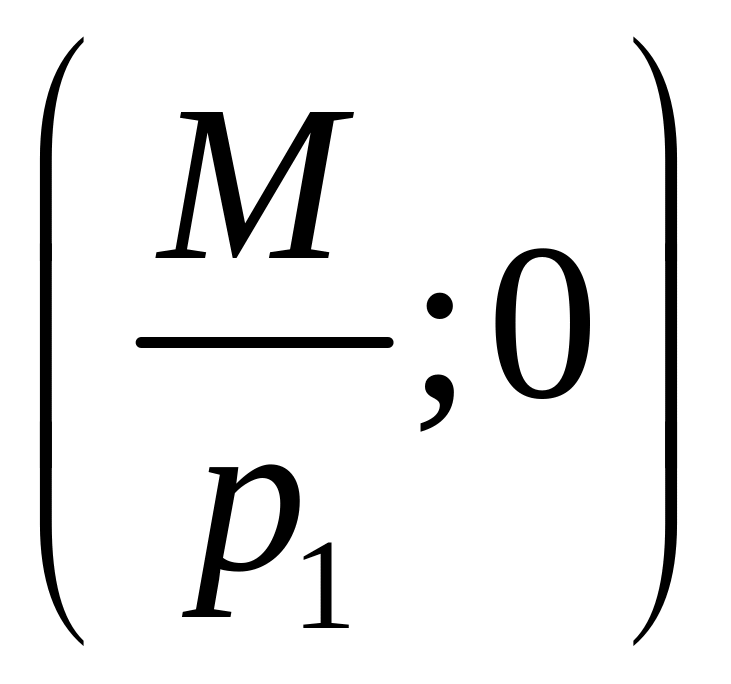и соответственно, т.е. , а .

О трезок прямой называется бюджетной линией. Отметим, что тангенс наклона бюджетной линии , т.е. .

Задача 4. Построить бюджетное множество, которое отражает покупательные возможности потребителя двух товаров, если на приобретение этих товаров расходуется не более  ден. ед. Известно, что цены товаров равны  ден. ед. и  ден. ед. соответственно.

4.1. ;	4.6. ;
4.2. ;	4.7. ;
4.3. ;	4.8. ;
4.4. ;	4.9. ;
4.5. ;	4.10. .