2.6. Теория массового обслуживания

Теория систем массового обслуживания (СМО) или теория очередей, начала развиваться в начале 20 века. Основателем СМО считается математик Иохансен, сформулировавший в 1907 году теоретические предпосылки новой теории.

Первые практические задачи теории массового обслуживания были рассмотрены сотрудником Копенгагенской телефонной компании, инженером Эрлангом (1878—1929) в период между 1908 и 1922 годами. Целью решения задач было упорядочить работу телефонной станции и заранее рассчитать качество обслуживания потребителей (очередь в ожидании) в зависимости от числа используемых устройств. В 1909 году Эрланг применил теорию вероятностей к исследованию зависимости обслуживания телефонных связей от числа поступающих на телефонную станцию вызовов. До сих пор эти идеи используются провайдерами сотовой связи.

В СССР развитием данной проблематики занимался математик Хинчин, одной из главных работ которого, является «Теория очередей».

Теория систем массового обслуживания посвящена разработке методов анализа, проектирования и рациональной организации систем, относящихся к различным областям деятельности, таким как связь, вычислительная техника, экономика, системы управления и организация производства, транспорт, торговля, здравоохранение, военное дело, логистика. Несмотря на все свое разнообразие, все приведенные системы обладают рядом типичных свойств, а именно:

• СМО представляют собой системы определенного специфического вида. Под системой понимается совокупность взаимосвязанных и целенаправленно взаимодействующих частей (элементов).

• СМО (системы массового обслуживания) - это модели системы, в которых с одной стороны возникают массовые запросы (требования) на выполнение каких-либо услуг, а с другой стороны происходит удовлетворение этих запросов.

• СМО представляет собой совокупность обслуживающего оборудования и персонала при соответствующей организации процесса обслуживания.

• Задать СМО  значит задать структуру системы и статистические характе-ристики последовательности поступления заявок и последовательности их обслуживания.

Каждая система массового обслуживания состоит из какого-то числа обслуживающих устройств, приборов, линий связи, кассовых аппаратов и тому подобное, восполняющих определенные операции. Все они в дальнейшем (тра-диционно) будут называться каналами обслуживания.

Обслуживанию подлежит поток заявок или требований, поступающих в системы. Заявки поступают чаще всего в случайные моменты времени. Длительность обслуживания каждой заявки так же является случайной величиной. В связи с этим работа системы протекает нерегулярно. В какие-то моменты каналы обслуживания простаивают, в другие моменты происходит накапливание заявок. Это приводит либо к отказу обслуживания каких-то заявок, либо к образованию из них очередей.

Для уменьшения степени влияния подобных негативных факторов разрабатываются рекомендации по создпнию рациональной организации системы в соответствии с требуемой пропускной способностью и другими характеристиками эффективности ее работы. Разработка подобных конкретных рекомендаций и методов расчета характеристик эффективности систем и есть предмет теории массового обслуживания.

Системы массового обслуживания (СМО)— это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания.      С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем, чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если таковое имеется в блоке ожидания.      Цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.

Примерами систем массового обслуживания могут служить:

1. магазины;

2. банки;

3. ремонтные мастерские;

4. почтовые отделения;

5. посты технического обслуживания автомобилей, посты ремонта автомобилей;

6. персональные компьютеры, обслуживающие поступающие заявки или требования на решение тех или иных задач;

7. аудиторские фирмы;

8. отделы налоговых инспекций, занимающиеся приемкой и проверкой текущей отчетности предприятий;

9. телефонные станции;

10. железнодорожные станции и т.д.

Основными компонентами системы массового обслуживания любого вида являются:

1. входной поток поступающих требований или заявок на обслуживание;

2. дисциплина очереди;

3. механизм обслуживания.

     Раскроем содержание каждого из указанных выше компонентов.       Входной поток требований (заявок). Для описания входного потока требуется задать вероятностный закон, определяющий последовательность моментов поступления требований на обслуживание и указать количество таких требований в каждом очередном поступлении. При этом, как правило, оперируют понятием «вероятностное распределение моментов поступления требований». Здесь могут поступать как единичные, так и групповые требования (требования поступают группами в систему). В последнем случае обычно речь идет о системе обслуживания с параллельно-групповым обслуживанием.       Дисциплина очереди — это важный компонент системы массово­го обслуживания, он определяет принцип, в соответствии с которым поступающие на вход обслуживающей системы требования подключаются из очереди к процедуре обслуживания.

Чаще всего используются дисциплины очереди, определяемые следующими правилами:     - первым пришел – первый обслуживаешься;     - пришел последним — обслуживаешься первым;     - случайный отбор заявок;     - отбор заявок по критерию приоритетности;      - ограничение времени ожидания момента наступления обслуживания (имеет место очередь с ограниченным временем ожидания обслуживания, что вполне и полностью ассоциируется с понятием «допустимая длина очереди»).       Механизм обслуживания определяется характеристиками самой процедуры обслуживания и структурой обслуживающей системы. К характеристикам процедуры обслуживания относятся: продол­жительность процедуры обслуживания и количество требований, удовлетворяемых в результате выполнения каждой такой процеду­ры.

Для аналитического описания характеристик процедуры обслу­живания обычно оперируют понятием «вероятностное распределение вре­мени обслуживания требований».      Следует отметить, что время обслуживания заявки зависит от характера самой заявки или требований клиента и от состояния и возможностей обслуживающей системы (каналов обслуживания).

В ряде случаев приходит­ся также учитывать вероятность выхода обслуживающего прибора по истечении некоторого ограниченного интервала времени (ремонт, технический осмотр).      Структура обслуживающей системы определяется количеством и взаимным расположением каналов обслуживания (механизмов, приборов и тому подобное.). Прежде всего, следует подчеркнуть, что система обслуживания как правило имеет не один канал обслуживания, а несколько; система такого рода способна обслуживать одновременно несколько требований (многоканальная СМО).

В этом случае все каналы обслуживания предлагают одни и те же услуги, и, следовательно, можно утверж­дать, что имеет место параллельное обслуживание.      Система обслуживания может состоять также из нескольких разнотипных каналов обслуживания, через которые должно пройти каж­дое обслуживаемое требование, то есть в обслуживающей системе про­цедуры обслуживания требований реализуются последовательно. Механизм обслуживания определяет характеристики (считывает меформацию) выходящего (обслуженного) потока требований.      После того как мы рассмотрели основные компоненты систем обслуживания, можно констатировать, что функциональные возможности любой системы массового обслуживания определяются следующими основными факторами:

1. вероятностным распределением моментов поступлений заявок на обслуживание (единичных или групповых);

2. вероятностным распределением времени продолжительности обслуживания;

3. конфигурацией обслуживающей системы (параллельное, последовательное или параллельно-последовательное обслуживание);

4. количеством и производительностью обслуживающих каналов;

5. дисциплиной очереди;

6. мощностью и возможностями источника требований.

     В качестве обязательных основных критериев эффективности функционирования систем массового обслуживания в зависимости от характера решаемой задачи могут выступать:

1. вероятность немедленного обслуживания поступившей заявки;

2. вероятность отказа в обслуживании поступившей заявки;

3. относительная и абсолютная пропускная способность системы;

4. средний процент заявок, получивших отказ в обслуживании;

5. среднее время ожидания в очереди;

6. средняя длина очереди;

7. средний доход от функционирования системы в единицу времени и тому подобное.

Таким образом предметом теории массового обслуживания является установление зависимости между факторами, определяющими функциональные возможности системы массового обслуживания, и эффективностью ее функционирования.

В подавляющем большинстве случаев все параметры, описывающие системы массового обслуживания, являются случайными величинами или функциями, поэтому эти системы относятся к стохастическим системам.       Независимо от характера самого процесса, протекающего в системе массового обслуживания, различают два основных вида СМО:      - системы с отказами, в которых заявка, поступившая в систему в момент, когда все каналы заняты, получает отказ и сразу же покидает очередь;      - системы с ожиданием (очередью), в которых заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь и ждет, пока не освободится один из каналов.       Системы массового обслуживания с ожиданием делятся на системы с ограниченным ожиданием и системы с неограниченным ожиданием (очередь безотказная).       Соответственно в системах с ограниченным ожиданием может ограничиваться:     - длина очереди;     - время пребывания в очереди.      В системах с неограниченным ожиданием заявка, стоящая в очереди, ждет обслуживание неограниченно долго, то есть. пока не подойдет очередь.       Все системы массового обслуживания можно различать по числу каналов обслуживания то есть:     - одноканальные системы;     - многоканальные системы.      Приведенная классификация СМО является весьма условной. На практике чаще всего системы массового обслуживания выступают в качестве смешанных систем.

Например, заявки ожидают начала обслуживания до определенного момента, после чего система начинает работать как система с отказами.       Напомним, что каналом обслуживания называется устройство в СМО, которое обслуживает заявку.

- СМО, содержащее один канал обслуживания, называется одноканальной.

- СМО содержащее более одного канала обслуживания – многоканальной. 

-  Если заявка, поступающая в СМО, может получить отказ в обслуживании (в силу занятости всех каналов обслуживания) и в случае отказа вынуждена покинуть СМО, то такая СМО называется СМО с отказами.

- Если в случае отказа в обслуживании заявки могут вставать в очередь, то такие СМО называются СМО с очередью (или с ожиданием). При этом различают СМО с ограниченной и неограниченной очередью. Очередь может быть ограничена как по количеству мест, так и по времени ожидания.

- Различают СМО открытого и замкнутого типа. В СМО открытого типа поток заявок не зависит от СМО. В СМО замкнутого типа обслуживается ограниченный круг клиентов, а число заявок может существенно зависеть от состояния СМО (например, бригада слесарей – наладчиков, обслуживающих станки на заводе).

СМОтакже могут также различаться по дисциплине обслуживания.

Если в СМО отсутствует приоритет, то заявки отбираются из очереди в канал по различным правилам например;

• Первым пришел – первым обслужен (FCFS – First Came – First Served)

• Последним пришел – первым обслужен (LCFS – Last Came – First Served)

• Первоочередное обслуживание требований с кратчайшей длительностью обслуживания (SPT/SJE)

• Первоочередное обслуживание требований с кратчайшей длительностью дообслуживания (SRPT)

• Первоочередное обслуживание требований с кратчайшей средней длительностью обслуживания (SEPT)

• Первоочередное обслуживание требований с кратчайшей средней длительностью дообслуживания (SERPT)

Важны также приоритеты, которые бывают двух типов – абсолютный и относительный.

Если требование в процессе обслуживания может быть удалено из канала и возвращено в очередь (либо вовсе покидает СМО) при поступлении требования с более высоким приоритетом, то такая система работает с абсолютным приоритетом. Если обслуживание любого требования, находящегося в канале не может быть прервано, то такая СМО работает с относительным приоритетом. Существуют также приоритеты, осуществляемые с помощью какого то конкретного правила или набора правил. Примером может служить приоритет, который изменяется с течением времени.

Чаще всего СМО описываются некоторыми параметрами, которые характеризуют эффективность работы системы.

– число каналов в СМО;

– интенсивность поступления в СМО заявок;

– интенсивность обслуживания заявок;

– коэффициент загрузки СМО;

– число мест в очереди;

– вероятность отказа в обслуживании поступившей в СМО заявки;

– вероятность обслуживания поступившей в СМО заявки (относительная пропускная способность СМО);

При этом:

(39)

А – среднее число заявок, обслуживаемых в СМО в единицу времени (абсолютная пропускная способность СМО)

(40) – среднее число заявок, находящихся в СМО

– среднее число каналов в СМО, обслуживающих заявки. Одновременно – это среднее число заявок, обслуживаемых в СМО за единицу времени. Величина это математическое ожидание случайного числа занятых обслуживанием n каналов.

, (41) где – вероятность нахождения системы в S_k состоянии.

– коэффициент занятости каналов

– среднее время ожидания заявки в очереди

– интенсивность ухода заявок из очереди

– среднее число заявок в очереди. Определяется как математическое ожидание случайной величины m – числа заявок, состоящих в очереди

(42) Где – вероятность нахождения в очереди i заявок;

– среднее время пребывания заявки с СМО

– среднее время пребывания заявки в очереди

В открытых СМО справедливы соотношения:

(43)

(44)

Эти соотношения известны в теории как формулы Литтла и применяются только для стационарных потоков заявок и обслуживания.

Рассмотрим некоторые типы СМО. При этом будет предполагаться, что плотность распределения промежутка времени между двумя последовательными событиями в СМО имеет показательное распределение, а все потоки являются простейшими.

Размеченный граф состояний одноканальной СМО представлен на рисунке

Рисунок 87. – Граф состояний одноканальной СМО

Здесь и – интенсивность потока заявок и выполнения заявок. Состояние системы S_o обозначает, что канал свободен, а S₁ – что канал, соответственно, занят обслуживанием заявки.

Система дифференциальных уравнений, названная в честь Колмогорова, для такой СМО имеет вид:

Рисунок 88.

где p_o(t) и p₁(t) – вероятности нахождения СМО в состояниях So и S1 соответственно. Уравнения для финальных вероятностей p_o и p₁ получим, приравнивая к нулю производные в первых двух уравнениях системы. В результате получим:

Рисунок 89.

Вероятность p₀ по своему смыслу - это вероятность обслуживания заявки p_обс, так как канал является свободным, а вероятность р₁ - по своему смыслу является вероятностью отказа, в обслуживании поступающей в СМО заявки р_отк, так как, канал занят обслуживанием предыдущей заявки.

Пусть СМО содержит n каких то каналов, а интенсивность входящего потока заявок равна , и интенсивность обслуживания заявки каждым каналом равна . Размеченный граф состояний системы можно увидеть на рисунке 90 .

Рисунок 90 – Граф состояний многоканальной СМО с отказами

Состояние S_0, естественно, означает, что все каналы свободны, состояние S_k (k = 1, n) означает, что обслуживанием заявок заняты k каналов.

Переход из одного состояния в другое соседнее правое происходит скачкообразно под воздействием входящего потока заявок интенсивностью независимо от числа работающих каналов (верхние стрелки).

Для перехода системы из одного состояния в соседнее левое неважно, какой именно канал освободится. Величина характеризует интенсивность обслуживания заявок при работе в СМО k каналов (на рисунке нижние стрелки).

Сравнивая графы легко увидеть, что многоканальная СМО с отказами является частным случаем системы рождения и гибели, (формулы Литтла) если в последней принять и

(45) При этом для нахождения финальных вероятностей можно воспользоваться вышеизложенными формулами (формулы Литтла). С их учётом получим:

(46) (47)

Эти формулы (46) и (47) называются формулами Эрланга – еще одного основателя теории массового обслуживания.

Вероятность отказа в обслуживании заявки р_отк равна вероятности того, что все каналы заняты, то есть система находится в состоянии S_n. Таким образом,

(48)

Относительную пропускную способность СМО можно найти:

(49)

Абсолютную пропускную способность можно найти:

(50)

Среднее число занятых обслуживанием каналов можно найти по формуле (50), однако можно сделать это проще. Так как каждый занятый канал в единицу времени обслуживает в среднем заявок, то конечно можно найти по формуле:

(51)

В СМО с ограниченной очередью число мест m в очереди ограничено. Следовательно, заявка, поступившая в момент времени, когда все места в очереди заняты, отклоняется и покидает СМО. Граф такой СМО представлен на рисунке 91.

S₀

Рисунок 91. – Граф состояний одноканальной СМО с ограниченной очередью

Состояния СМО представляются следующим образом:

S₀ – канал обслуживания свободен,

S₁ – канал обслуживания занят, но очереди нет,

S₂ – канал обслуживания занят, в очереди одна заявка,

S_k+1 – канал обслуживания занят, в очереди k заявок,

S_m+1 – канал обслуживания занят, все m мест в очереди заняты.

Для получения необходимых формул можно воспользоваться тем обстоятельством, что СМО на рисунке является частным случаем системы рождения и гибели, представленной на рисунке, если в последней принять и

(52)

(53)

(54)

Выражения для финальных вероятностей состояний рассматриваемой СМО можно найти из (54) и (53) с учётом (52). В результате получим:

Поступившая в СМО заявка получает отказ в обслуживании, если СМО находится в состоянии S_m+1, то есть вероятность отказа в обслуживании заявки равна:

(55)

(56)

Таким образом относительная пропускная способность СМО равна:

(57)

Тогда абсолютная пропускная способность равна:

(58)

Ну и среднее число заявок, стоящих в очереди L_оч, находится по формуле

(59)

и может быть записано в виде:

(60)

При формула принимает вид:

(61)

– среднее число заявок, находящихся в СМО, находится по формуле 62.

(62)

и тогда может быть записано в виде:

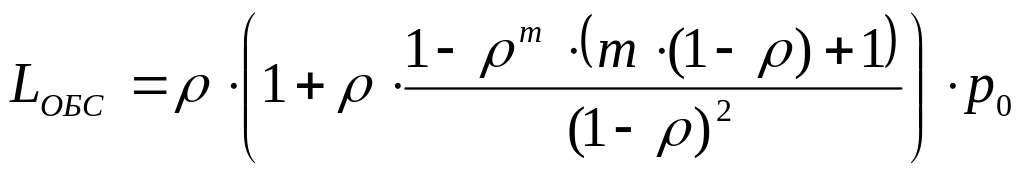(63)

При , получим:

(64)

Среднее время пребывания заявки в СМО и в очереди находится по вышеизложенным формулам.

Граф такой СМО изображён на рисунке.

Рисунок 92. – Граф состояний одноканальной СМО с неограниченной очередью

Все характеристики такой СМО можно получить из вышеизложенных формул, полагая в них . При этом необходимо различать два существенно разных случая то есть: а) ; б) . В первом случае, как это видно из формул (22), (23), р₀ = 0 и p_k = 0 (при всех конечных значениях k). Это означает, что при очередь естественно неограниченно возрастает, то есть этот случай практического интереса не представляет.

Рассмотрим случай, когда . Формулы при этом запишутся в виде:

(65)

(66)

Поскольку в СМО отсутствует ограничение на длину очереди как таковой, то любая заявка может быть обслужена, то есть относительная пропускная способность равна:

(67)

Тогда абсолютная пропускная способность равна:

(68)

А среднее число заявок в очереди получим из формулы при :

(69)

При этом среднее число обслуживаемых заявок есть:

(70)

Среднее число заявок, находящихся в СМО:

(71)

Ну и среднее время пребывания заявки в СМО и в очереди определяются этими формулами.

Пусть на вход СМО, имеющей каналов обслуживания, поступает пуассоновский поток заявок с интенсивностью . Интенсивность обслуживания заявки каждым каналом равна , а максимальное число мест в очереди равно .

Граф такой системы представлен на рисунке 93.

Рисунок 93. – Граф состояний многоканальной СМО с ограниченной очередью

– все каналы свободны, очереди нет;

– заняты l каналов (l = 1, n), очереди нет;

- заняты все n каналов, в очереди находится i заявок (i = 1, m).

Сравнение графов на рисунке 89 и рисунке 93 показывает, что последняя система является частным случаем системы размножения и гибели, если в ней сделать следующие замены (левые обозначения относятся к системе рождения и гибели):

Рисунок 94.

Выражения для финальных вероятностей можно легко найти из формул. В результате получим:

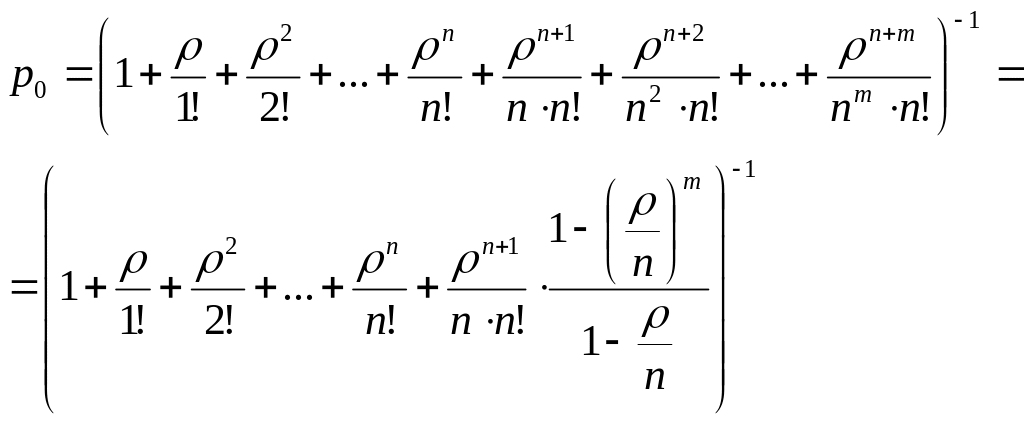
Рисунок 95.

Тогда образование очереди происходит, когда в момент поступления в СМО очередной заявки все каналы заняты, то есть в системе находятся либо n, либо (n+1),…, либо (n + m – 1) заявок. Так как эти события несовместны, то вероятность образования очереди p_оч равна сумме соответствующих вероятностей :

(72)

Отказ в обслуживании заявки происходит, когда все m мест в очереди заняты, т.е.:

(73)

Относительная пропускная способность равна:

(74)

Абсолютная пропускная способность:

(75)

Среднее число заявок, находящихся в очереди, определяется по формуле (71) и может быть записано в виде:

(76)

Среднее число заявок, обслуживаемых в СМО, может быть записано в виде:

(77)

Среднее число заявок, находящихся в СМО:

(78)

Среднее время пребывания заявки в СМО и в очереди определяется вышеизложенными формулами.

Граф такой СМО изображен на рисунке 96 и получается из графа на рисунке 7 при .

Рисунок 96 – Граф состояний многоканальной СМО с неограниченной очередью

Формулы для финальных вероятностей можно получить из формул для n-канальной СМО с ограниченной очередью при . При этом следует иметь в виду, что при вероятность р₀ = р₁=…= p_n = 0, т.е. очередь неограниченно возрастает. Следовательно, этот случай практического интереса не представляет и ниже рассматривается лишь случай . При из этого получим:

(79)

Формулы для остальных вероятностей имеют тот же вид, что и для СМО с ограниченной очередью:

(80)

Из вышеизложенных формул получим выражение для вероятности образования очереди заявок:

(81)

Поскольку очередь не ограничена, то вероятность отказа в обслуживании заявки:

(82)

Относительная пропускная способность:

(83)

Абсолютная пропускная способность:

(84)

Из формул при получим выражение для среднего числа заявок в очереди:

(85)

Среднее число обслуживаемых заявок определяется формулой:

(86)

Отличие такой СМО от СМО, рассмотренной выше, состоит в том, что время ожидания обслуживания, когда заявка находится в очереди, считается случайной величиной, распределённой по показательному закону с параметром , где – среднее время ожидания заявки в очереди, а – имеет смысл интенсивности потока ухода заявок из очереди. Граф такой СМО изображён на рисунке 9.

Рисунок 97. – граф многоканальной СМО с ограниченной очередью и ограниченным временем ожидания в очереди

Остальные обозначения имеют здесь тот же смысл, что и в подразделе.

Сравнение графов на рис. 97  и показывает, что последняя система является частным случаем системы рождения и гибели, если в ней сделать следующие замены (левые обозначения относятся к системе рождения и гибели):

Рисунок 98

Выражения для финальных вероятностей легко найти из формул и с учетом. В результате получим:

,

Рисунок 99.

где . Вероятность образования очереди определяется формулой:

(87)

Отказ в обслуживании заявки происходит, когда все m мест в очереди заняты, то есть вероятность отказа в обслуживании:

(88)

Относительная пропускная способность:

(89)

Абсолютная пропускная способность:

(90)

Среднее число заявок, находящихся в очереди, находится по формуле и равно:

(91)

Среднее число заявок, обслуживаемых в СМО, находится по формуле и равно:

(92)

Среднее время пребывания заявки в СМО складывается из среднего времени ожидания в очереди и среднего времени обслуживания заявки:

(93)

Переход СМО из одного состояния в другое, как мы уже упоминали, происходит случайным образом и представляет собой случайный процесс. Работа СМО это случайный процесс с дискретными состояниями, поскольку его возможные состояния во времени можно заранее перечислить. Как мы уже упоминали переход из одного состояния в другое, происходит скачкообразно, в случайные моменты времени, поэтому он называется процессом с непрерывным временем.

Таким образом, работа СМО представляет собой случайный процесс с дискретными состояниями и непрерывным; временем. Конкретный пример - в процессе обслуживания оптовых покупателей на фирме «Кристалл» в Москве можно фиксировать заранее все возможные состояния простейших СМО, которые входят во весь цикл, коммерческого обслуживания от момента заключения договора на поставку ликероводочной продукции, ее оплаты, оформления документов, отпуска и получения продукции, догрузки и вывоза со склада готовой продукции.

Из множества разновидностей случайных процессов наибольшее распространение в коммерческой деятельности получили такие процессы, для которых в любой момент времени характеристики процесса в будущем зависят только от его состояния в настоящий момент и не зависят от предыстории от прошлого (Марковский процесс). Например, возможность получения с завода «Кристалл» ликероводочной продукции зависит от наличия ее на складе готовой продукции, то есть его состояния в данный момент, и не зависит от того, когда и как получали и увозили в прошлом эту продукцию другие покупатели.

Такие случайные процессы называются процессами без последствия, или Марковскими, в которых при фиксированном настоящем будущее состояние СМО не зависит от прошлого. Случайный процесс, протекающий в системе, называется Марковским случайным процессом, или «процессом без последствия», если он обладает следующим свойством: для каждого момента времени t₀ вероятность любого состояния t > t₀ системы S_i, - в будущем (t >t_Q) зависит только от ее состояния в настоящем (при t = t₀) и не зависит от того, когда и каким образом система пришла в это состояние, то есть оттого, как развивался процесс в прошлом.

Такие Марковские случайные процессы делятся на два класса: процессы с дискретными и непрерывными состояниями. Процесс с дискретными состояниями возникает в системах, обладающих только некоторыми фиксированными состояниями, между которыми возможны скачкообразные переходы в некоторые, заранее не известные моменты времени. Теперь рассмотрим пример процесса с дискретными состояниями. В офисе фирмы имеются два стационарных телефона. Возможны только следующие состояния у этой системы обслуживания: S_o-телефоны свободны; S_l - один из телефонов занят; S₂- оба телефона заняты.

Процесс, протекающий в этой системе, состоит в том, что система случайным образом переходит скачком из одного дискретного состояния в другое.

Процессы с непрерывными состояниями отличаются непрерывным плавным или ритмичным переходом из одного состояния в другое. Эти процессы более характерны для технических устройств (конвеер), нежели для экономических объектов, где обычно лишь приближенно можно говорить о непрерывности процесса (например, непрерывном расходовании запаса товара), тогда как фактически всегда процесс имеет дискретный характер, поэтому далее мы будем рассматривать только процессы с дискретными состояниями.

Марковские случайные процессы с дискретными состояниями в свою очередь подразделяются на процессы с дискретным временем и процессы с непрерывным временем. В первом случае переходы из одного состояния в другое происходят только в определенные, заранее фиксированные моменты времени, тогда как в промежутки между этими моментами система сохраняет свое стабильное состояние. Во втором случае переход системы из состояния в состояние естественно может происходить в любой случайный момент времени.

На практике процессы с непрерывным временем встречаются значительно чаще, поскольку переходы системы из одного состояния в другое обычно происходят не в какие-то фиксированные моменты времени, а в любые случайные моменты времени.

Для описания процессов с непрерывным временем используется модель в виде так называемой марковской цепи с дискретными состояниями системы, либо непрерывной марковской цепью.

Теперь рассмотрим математическое описание Марковского случайного процесса с дискретными состояниями системы S_o, S_l,S₂ и с непрерывным временем. Полагаем, что все переходы системы массового обслуживания из состояния S_i в состояние Sj происходят под воздействием самых простейших потоков событий с интенсивностями л_ij, а обратный переход под воздействием другого потока л_ij,. Введем обозначение p_i как вероятность того, что в момент времени t система находится в состоянии S_i. Для любого момента времени t справедливо записать нормировочное условие - сумма вероятностей всех состояний равна 1:

₂ Уp_i(t)=p₀(t)+ p₁(t)+ p₂(t)=1 (94)

ⁱ⁼⁰

Теперь проведем анализ системы в момент времени t, задав малое приращение времени Дt, и найдем вероятность р₁ (t + Дt) того, что система в момент времени (t + Дt) будет находиться в состоянии S₁ которое достигается разными вариантами:

а) система в момент t с вероятностью p₁(t) находилась в состоянии S₁ и за малое приращение времени Дt так и не перешла в другое соседнее состояние ни в S₀, ни b S₂. Вывести систему из состояния S₁ можно суммарным простейшим потоком c интенсивностью (л₁₀ + л₁₂), поскольку суперпозиция простейших потоков и также является простейшим потоком. Тогда на этом основании вероятность выхода из состояния S₁ за малый промежуток времени Д t приближенно равна (л₁₀ + л₁₂)* Д t. И тогда вероятность невыхода из этого состояния равна [1 -(л₁₀ +л₁₂)* Д t]. B соответствии с этим вероятность того, что система останется в состоянии Si на основании теоремы умножения вероятностей, равна:

p₁(t) [1 - (л₁₀ + л₁₂)* Д t]; (95)

б) система находилась в соседнем состоянии S_o и за малое время Д t перешла в состояние S_o. Переход системы происходит под воздействием потока л₀₁ с вероятностью, приближенно равной л₀₁Д t

Вероятность того, что система будет находиться в состоянии S₁, в этом варианте равна p_o(t) л ₀₁ Д t;

в) система находилась в состоянии S₂ и за время Д t перешла в состояние S₁ под воздействием потока интенсивностью л ₂₁ с вероятностью, приближенно равной л₂₁Д t. Вероятность того, что система будет находиться в состоянии S₁, равна p₂(t) л₂₁Д t.

Применяя теорему сложения вероятностей для этих вариантов, получим выражение:

p₂(t + Дt)= p₁(t) [1 -(л₁₀ + л₁₂)* Д t] + p_o(t) л ₀₁ Д t + p₂(t) л₂₁Д t , (96)

которое можно записать иначе:

p₂(t + Дt)- p₁(t)/ Д t = p_o(t) л ₀₁ + p₂(t) л₂₁- p₁(t) (л₁₀ + л₁₂) . (97)

Переходя к пределу при Дt -> 0, приближенные равенства перейдут в точные, и тогда получим производную первого порядка

dp₂/dt = p₀ л ₀₁ + p₂ л₂₁ -p₁ (л₁₀ + л₁₂) , (98)

что является дифференциальным уравнением.

Проводя рассуждения аналогичным образом для всех других состояний системы, получим систему дифференциальных уравнений, которые называются уравнениями А. Н. Колмогорова:

dp₀ /dt = p₁ л ₁₀ , (99)

dp₁ /dt = p₀ л ₀₁ +p₂ л₂₁ -p₁ (л₁₀ +л₁₂) , (100)

dp₂ /dt= p₁ л ₁₂ +p₂ л_{21 . (101)}

Однако для составления уравнений Колмогорова существуют общие правила.

Уравнения Колмогорова позволяют вычислить все возможные вероятности состояний СМО S_i в функции времени p_i(t). В теории случайных процессов показано, что если число состояний системы конечно, а из каждого из них можно перейти в любое другое состояние, то тогда существуют предельные (финальные) вероятности состояний, которые показывают на среднюю относительную величину времени пребывания системы, в этом состоянии.

Если предельная вероятность состояния S₀ - равна p₀ ⁼ 0,2, то, следовательно, в среднем 20% времени, или 1/5 рабочего времени, система находится в состоянии S_o. Например, при отсутствии заявок на обслуживание к = 0, р₀ = 0,2,; следовательно, в среднем 2 ч в день система находится в состоянии S_o и простаивает, если продолжительность рабочего дня составляет 10 ч.

Поскольку предельные вероятности системы постоянны, то заменив в уравнениях Колмогорова соответствующие производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим СМО.

Такую систему уравнений составляют по размеченному графу состояний СМО по следующим правилам: слева от знака равенства в уравнении стоит предельная вероятность р_i рассматриваемого состояния Si умноженная на суммарную интенсивность всех потоков, выводящих (выходящие стрелки) изданного состояния S_i систему, а справа от знака равенства сумма произведений интенсивности всех потоков, входящих (входящие стрелки) в состояние Si систему, на вероятность тех состояний, из которых эти потоки исходят. Для решения подобной системы необходимо добавить еще одно уравнение, определяющее нормировочное условие, поскольку сумма вероятностей всех состояний СМО равна 1: _n

Уp_i(t) = 1 (102)

ⁱ⁼¹

Например, для СМО, имеющей размеченный граф из трех состояний S_o, S₁, S₂, система уравнений Колмогорова, составленная на основе изложенного правила, имеет следующий вид:

Для состояния S_o> p₀ л ₀₁ = p₁ л _{10 (103)}

Для состояния S₁> p₁ (л₁₀ +л₁₂) = p₀ л ₀₁ +p₂ л_{21 (104)}

Для состояния S₂> p₂ л₂₁ = p₁ л _{12 (105)}

p₀ +p₁ +p₂ =1 (106)

dp ₄(t) /dt= л₃₄ p₃(t) - л₄₃ p₄(t) , (107)

p₁(t) + p₂(t) + p₃(t) + p₄(t) = 1 . (108)

К этим уравнениям надо добавить еще и начальные условия. Так например, если при t = 0 система S находится в состоянии S_1, то начальные условия можно записать так:

p₁(0)=1, p₂(0)= p₃(0)= p₄(0)=0 . (109)

Переходы между этими состояниями СМО происходит под воздействием поступления заявок и их обслуживания. Вероятность перехода в случае, если поток событий простейший, определяется вероятностью появления события в течение какого – то времени Д t, то есть величиной элемента вероятности перехода л_ij Д t, где л_ij интенсивность потока событий, переводящих систему из состояния i в состояние i (по соответствующей стрелке на графе состояний).

Если все потоки событий, переводящие систему из одного состояния в другое, простейшие, то процесс, протекающий в системе, будет естественно Марковским случайным процессом, то есть процессом без последствия. В этом случае поведение системы достаточно просто определяется если известны интенсивность всех этих простейших потоков событий. Например, если в системе протекает марковский случайный процесс с непрерывным временем, то, записав систему уравнений Колмогорова для вероятностей состояний и проинтегрировав эту систему при заданных начальных условиях, получим все возможные вероятности состояний как функции времени:

p_i(t), p₂(t),…., p_n(t) . (110)

Во многих случаях на практике оказывается, что вероятности состояний как функции времени ведут себя таким образом, что реально существует

lim p_i(t) = p_i (i=1,2,…,n) ; t>? (111)

независимо от вида начальных условий. В этом случае говорят, что существуют предельные вероятности состояний системы при t->? и в системе устанавливается некоторый предельный стационарный режим. При этом система случайным образом меняет свои, состояния, однако каждое из этих состояний осуществляется с некоторой постоянной вероятностью, которая определяется средним временем пребывания системы в каждом из состояний.

Вычислить предельные вероятности состояния р_i можно, если в системе положить все производные равными 0, поскольку в уравнениях Колмогорова при t-> ? зависимость от времени пропадает. Тогда система дифференциальных уравнений превращается в систему обычных линейных алгебраических уравнений, которая совместно с нормировочным условием и позволяет вычислить все предельные вероятности состояний.

Правильная или наиболее удачная экономико-математическая постановка задачи в значительной степени определяет полезность рекомендаций по совершенствованию систем массового обслуживания в коммерческой деятельности и решения в виде программного обеспечения.

В связи с этим необходимо тщательно проводить статистическое наблюдение за процессом в системе, поиска и выявления существенных связей, формирования проблемы, выделения цели, определения показателей и выделения экономических критериев оценки работы СМО. В этом случае в качестве наиболее точного, интегрального показателя могут выступать затраты, с одной стороны, СМО коммерческой деятельности как обслуживающей системы, а с другой - затраты связанные с заявками, которые могут иметь разную по своему физическому содержанию природу.

Повышение эффективности в любой сфере деятельности трудовая теория (К. Маркс, А. Смит, Д. Риккардо), в конечном счете, рассматривала как экономию времени и усматривал в этом один из важнейших экономических законов. К. Маркс писал, что экономия времени, равно как и планомерное распределение рабочего времени по различным отраслям производства, остается первым экономическим законом на основе коллективного производства. И этот закон проявляется во всех сферах общественной деятельности.

В рыночной экономике для товаров, в том числе и денежных средств, поступающих в коммерческую сферу, критерий эффективности связан со временем и скоростью обращения товаров и определяет интенсивность поступления денежных средств в банк. Время и скорость обращения, являясь показателями коммерческой деятельности, характеризирует эффективность использования средств, вложенных в товарные запасы. Товарооборачиваемость таким образом отражает среднюю скорость реализации среднего товарного запаса. Показатели товарооборачиваемости и уровня запасов тесно связаны с известными моделями (особенно логистическими). Таким образом, можно проследить и установить взаимосвязи между всеми показателями коммерческой деятельности с временными характеристиками.

Следовательно, эффективность работы коммерческого предприятия или организации складывается из совокупности времени выполнения отдельных операций обслуживания, в то же время для населения затраты времени включают время на дорогу, посещение магазина, столовой, кафе, ресторана, ожидание начало обслуживания, ознакомление с меню, выбор продукции, расчет и так далее. Проведенные исследования структуры затрат времени населения свидетельствует о том, что значительная его часть расходуется весьма нерационально. Заметим, что коммерческая деятельность, в конечном счете, должна быть направлена на удовлетворение потребности человека. Поэтому усилия моделирования таких СМО должны включать анализ затрат времени по каждой элементарной операции обслуживания. С помощью соответствующих методов и следует создавать модели связи показателей СМО.

Это обусловливает необходимость применять наиболее общие и известные экономические показатели, такие как товарооборот, прибыль, издержки обращения, рентабельность и другие, увязывать в экономико-математических моделях с дополнительно возникающей группой показателей, определяемых спецификой обслуживающих систем и вносимых собственно спецификой теории массового обслуживания.

Например, особенностями показателей СМО с отказами являются: время ожидания заявок в очереди Т_оч=0, поскольку по своей природе в таких системах существование очереди невозможно, то L_оч=0 и, следовательно, вероятность ее образования Р_оч=0. По числу заявок k определятся режим работы системы, ее состояние: при k=0 - простой каналов, при 1<k<n - обслуживание заявок, при k>n - обслуживание и отказ. Показателями таких СМО являются вероятность отказа в обслуживании Р_отк, вероятность обслуживания Р_обс, среднее время простоя канала t_пр, среднее число занятых n_з и свободных каналов n_св, среднее обслуживания t_обс, абсолютная пропускная способность А.

Для СМО с неограниченным ожиданием характерно, что вероятность обслуживания заявки Р_обс=1, поскольку длина очереди и время ожидания начала обслуживания не ограничены, т.е. формально L_оч>? и Т_оч>?. В системах возможны следующие режимы работы: при k=0 наблюдается простой каналов обслуживания, при 1<k?n - обслуживание и при k>n - обслуживание и очередь. Показателями таких эффективности таких СМО являются среднее число заявок в очереди L_оч, среднее число заявок в системе k, среднее время пребывания заявки в системе Т_смо, абсолютная пропускная способность А.

В СМО с ожиданием с ограничением на длину очереди, если число заявок в системе k=0, то наблюдается простой каналов, при 1<k?n- обслуживание, при n<k<n+m - обслуживание и очередь и при k>n+m- обслуживание, очередь и отказ в ожидании обслуживания. Показателями эффективности таких СМО являются вероятность отказа в обслуживании Р_отк - вероятность обслуживания Р_обс, среднее число заявок в очереди L_оч, среднее число заявок в системе L_смо среднее время пребывания заявки в системе Т_смо, абсолютная пропускная способность А.

Таким образом, перечень характеристик систем массового обслуживания можно представить следующим образом: среднее время обслуживания - t_обс; среднее время ожидания в очереди - Т_оч; среднее пребывания в СМО - Т_смо; средняя длина очереди - L_оч; среднее число заявок в СМО- L_смо; количество каналов обслуживания - n; интенсивность входного потока заявок - л; интенсивность обслуживания - м; интенсивность нагрузки - с; коэффициент нагрузки - б; относительная пропускная способность - Q; абсолютная пропускная способность - А; доля времени простоя в СМО - Р₀; доля обслуженных заявок - Р_обс; доля потерянных заявок - Р_отк, среднее число занятых каналов - n_з; среднее число свободных каналов - n_св; коэффициент загрузки каналов - К_з; среднее время простоя каналов - t_пр.

Следует заметить что, иногда достаточно использовать немного (около десяти основных показателей), чтобы выявить слабые места и разработать рекомендации по совершенствованию СМО.

Это часто связано с решением вопросов согласованной работы всей цепочки или совокупностей СМО.

Например, в коммерческой деятельности обязательно необходимо учитывать еще и экономические показатели СМО: общие затраты - С; издержки обращения - С_ио, издержки потребления - С_ип, затраты на обслуживание одной заявки - С₁, убытки, связанные с уходом заявки, - С_у1, затраты на эксплуатацию канала - С_к, затраты простоя канала - С_пр, капитальные вложения - С_кап, приведенные годовые затраты - С_пр, текущие затраты - С_тек, доход СМО в единицу времени - Д₁

В процессе постановки задач необходимо раскрыть все взаимосвязи показателей СМО, которые по своей базовой принадлежности можно разделить на две группы: первая связана с издержками обращения С_ио, которые определяются числом занятых обслуживанием каналов, затратами на содержание СМО, интенсивностью обслуживания, степенью загрузки каналов, эффективностью их использования, пропускной способностью СМО и др.; вторая группа показателей определяется издержками собственно заявок С_ип, поступающих на обслуживание, которые образуют входящий поток, ощущают эффективность обслуживания и связаны с такими показателями, как длина очереди, время ожидания обслуживания, вероятность отказа в обслуживании, время пребывания заявки в СМО и др.

Эти группы показателей противоречивы в том смысле, что улучшение показателей одной группы (противоречие клиент – бизнесмен), например, сокращение длины очереди или времени ожидания в очереди путем увлечения числа каналов обслуживания (официантов, поваров, грузчиков, кассиров), связано с ухудшением показателей группы, поскольку это может привести к увеличению времени простоев каналов обслуживания, затрат на их содержание и так далее. В связи с этим формализации задач обслуживания вполне естественно стремление построить СМО таким образом, чтобы установить разумный компромисс между показателями собственно заявок и полнотой использования возможностей системы. С этой целью необходимо выбрать обобщенный, интегральный показатель эффективности СМО, включающий одновременно претензии и возможности обеих групп. В качестве такого показателя может быть выбран критерий экономической эффективности, включающий как издержки обращения С_ио, так и издержки заявок С_ип, которые будут иметь оптимальное значение при минимуме общих затрат С и системы ограничений (линейное программирование). На этом основании целевую функцию задачи можно записать так:

С= (С_ио+С_ип) >min (112)

Так как всегда издержки обращения включают затраты, связанные с эксплуатацией СМО - С_экс и простоем каналов обслуживания - С_пр, а издержки заявок включают потери, связанные с уходом не обслуженных заявок - С_нз, и с пребыванием в очереди - С_оч., тогда целевую функцию можно переписать с учетом этих показателей таким образом:

С={(С_прn_св+С_экзn_з) + С_очР_обсл (Т_оч + t_обс) + С_изР_откл}>min. (113)

В зависимости от поставленной задачи в качестве изменяющихся, варьируемых, то есть управляемых, показателей могут быть: количество каналов обслуживания, организация каналов обслуживания (параллельно, последовательно, смешанным образом), дисциплина очереди, приоритетность обслуживания заявок, взаимопомощь между каналами и так далее. Часть показателей в задаче могут фигурировать в качестве неуправляемых, которые обычно являются исходными данными. В качестве критерия эффективности в целевой функции могут быть так же товарооборот, прибыль, или доход, или например рентабельность, тогда оптимальные значения управляемых показателей СМО находятся, очевидно, уже при максимизации, как в предыдущем варианте.

В некоторых случаях можно пользоваться и другим вариантом записи целевой функции:

С={С_экзn_з+C_пр(n-n _з)+C_отк*Р_отк*л+С_сист* n_з}>min (114)

В качестве общего критерия также может быть выбран, например, уровень культуры обслуживания покупателей на предприятиях, тогда целевая функция может быть представлена следующей моделью:

К_об=[(З_пу*К_у)+(З_пв*К_в)+(З_пд*К_д)+(З_пз*К_з)+(З_по*К₀)+(З_кт*К_кт)]*К_мп, (115)

где З_пу - значимость показателя устойчивости ассортимента товаров;

К_у - коэффициент устойчивости ассортимента товаров;

З_пв - значимость показателя внедрения прогрессивных методов продажи товаров;

К_в - коэффициент внедрения прогрессивных методов продажи товаров;

З_пд - значимость показателя дополнительного обслуживания;

К_д - коэффициент дополнительного обслуживания;

З_пз - значимость показателя завершенности покупки;

К_з - коэффициент завершенности покупки;

З_по - значимость показателя затрат времени на ожидание в обслуживании;

К_о - показатель затрат времени на ожидание обслуживания;

З_кт - значимость показателя качества труда коллектива;

К_кт - коэффициент качества труда коллектива;

К_мп - показатель культуры обслуживания по мнению покупателей;

Для анализа СМО, конечно, можно выбирать и другие критерии оценки эффективности работы СМО. Например, в качестве такого критерия для систем с отказами можно выбирать вероятность отказа Р_отк, значение которого не превышало бы какой то заранее заданной величины. Например, требование Р_отк<0,1 означает, что не менее чем в 90% случаев система будет справляться с обслуживанием потока заявок при заданной интенсивности л. Можно также ограничить среднее время пребывания заявки в очереди или в системе. В качестве показателей, которые должны подлежать определению, могут выступать: либо число каналов n при заданной интенсивности обслуживания м, либо интенсивность м при заданном числе каналов.

Наконец после построения целевой функции необходимо определить условия решения задачи, найти ограничения, установить исходные значения показателей, выделить неуправляемые показатели, построить или подобрать совокупность моделей взаимосвязи всех показателей для анализируемого типа СМО, чтобы в конечном итоге найти оптимальные значения управляемых показателей, например количество поваров, официантов, кассиров, грузчиков, объемы складских помещений и так далее.

Если система S может переходить в другое состояние случайным образом в произвольный момент времени, то тогда говорят о случайном процессе с непрерывным временем. В отсутствии последствия такой процесс называется непрерывной марковской цепью. При этом вероятности переходов для любых i и j в любой момент времени равны нулю (в силу непрерывности времени). По этой причине вместо вероятности перехода вводится величина - плотность вероятности перехода из состояния в состояние , определяемая как предел:

(116)

Если эти величины не зависят от t, то марковский процесс называется однородным. Если за время система может изменить свое состояние не более чем один раз, то говорят, что случайный процесс является ординарным. Величину принято называть интенсивностью перехода системы из S_i в S_j. На графе состояний системы численные значения всегда ставят рядом со стрелками, показывающими переходы в вершины графа.

Зная интенсивности переходов можно найти величины p₁(t), p₂(t),…, p_n(t) – вероятности нахождения системы S в состояниях S₁, S₂,…, S_n соответственно. При этом выполняется условие:

(117)

Распределение таких вероятностей состояний системы, которое можно характеризовать вектором , называется стационарным, если оно не зависит от времени, то есть все компоненты вектора являются константами.

В свою очередь состояния S_i и Sj называются сообщающимися, если возможны переходы .

Если состояние S_i называется существенным, если всякое S_j, достижимое из S_i, является сообщающимся с S_i. Тогда состояние S_i называется несущественным, если оно не является существенным.

Если существуют предельные вероятности состояний системы то:

, (118)

не зависящие от начального состояния системы, тогда говорят, что при в системе устанавливается стационарный режим.

Система, в которой существуют предельные (финальные), вероятности состояний системы, называется эргодической, и соответственно протекающий в ней случайный процесс эргодическим.

Теорема 1. Если S_i – несущественное состояние, то то есть при система выходит из любого несущественного состояния.

Теорема 2. Чтобы система с конечным числом состояний имела единственное предельное распределение вероятностей состояний, необходимо и достаточно, чтобы все ее существенные состояния сообщались между собой.

Если случайный процесс, происходящий в системе с дискретными состояниями является непрерывной марковской цепью, то для вероятностей p₁(t), р₂(t),…, p_n(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова. При составлении уравнений удобно пользоваться графом состояний системы. В левой части каждого из них стоит производная вероятности какого-то (j-го) состояния. В правой части – сумма произведений вероятностей всех состояний, из которых возможен переход в данное состояние, на интенсивности соответствующих потоков, минус суммарная интенсивность всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния.