2. Факторні методи визначення екстремуму

Ідея методу – пробні досліди ставляться у відповідності з ПФЕ.

Метод Бокса-Уілсона (Метод крутого сходження)

В околі точки Ко ставимо ПФЕ. Нехай отримано

a_j – пропорційні проекціям вектора-градієнта на осі фактори

1. для знаходження координат точки Кі у напрямі екстремуму необхідно визначити взаємозв’язок між кроком зміни j-тої незалежної величини у нормальній і кодованій системі координат

2. вибираємо найбільш суттєвий фактор, напр. К за абсолютною величиною фактора

3. з фізичних величин вибираємо крок зміни 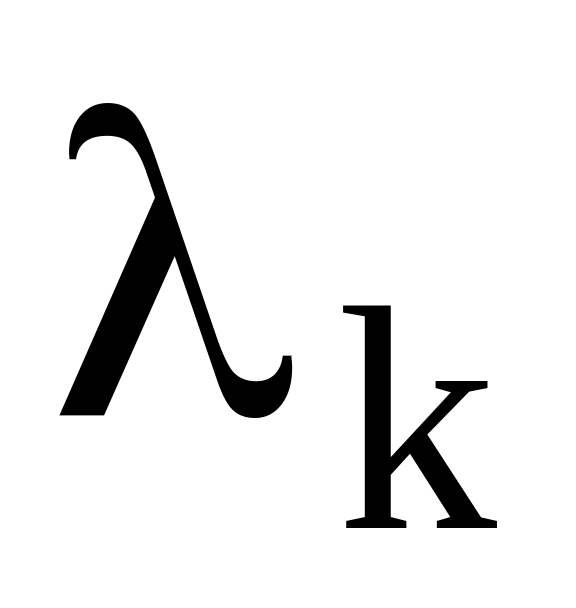у звичайному масштабі

4. встановлюємо зв’язок між і (нормованій системі)

Використаємо

,

x_k – кодована система; X_k – звичайна система

Нехай К₅ точка екстремуму, тоді

Тоді у кодованій системі координат

( * )

Але для кодованого значення К-го фактора точки К₅ можна записати

Оскільки точка К₀ лежить у центрі плану, то , маємо

( ** )

Зпівставивши (*) і (**), отримаємо

5. Значення у натуральній системі

6. Використовуючи співвідношення

знаходимо координати точок, які лежать у напрямі градієнта.

Признаком досягнення екстремуму є не значимість коефіцієнтів і різке зростання коефіцієнтів при парних взаємодіях факторів.

Приклад:

Знайти екстремальну область, якщо

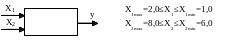
	X1	X2	Y
1	–	–	95
2	+	–	90
3	–	+	85
4	+	+	82

Визначаємо координати базової точки та інтервали зміни факторів

;

;

;

В околі базової точки ( ) у відповідності ПФЕ провели експеримент

Знаходимо а₀=88,0; а₁= - 2,0; а₂= - 4,5 та отримаємо

.

Найбільш суттєвий фактор х₂, бо .

Вибираємо крок зміни фактора х₂ :

Визначаємо крок зміни факторів у кодованій системі координат

Знаходимо крок зміни фактора х₁

Отже

Знаходимо .

Нова базова точка і цикл повторюємо.

Признаком досягнення екстремуму є не значимість лінійних коефіцієнтів математичної моделі на одному з етапів і різке зростання коефіцієнтів при парних взаємодіях факторів.

Лекція 3 оптимізація технологічних процесів деревообробки з застосуванням методів лінійного програмування

Задачі лінійного програмування (ЗЛП) складають великий клас дослідження операцій. До них зокрема відносяться:

• оптимальне завантаження станків;

• формування виробничої програми деревообробних підприємств;

• планування розкрою листових і круглих деревинних матеріалів та ряд інших задач.

Особливість структури ЗЛП полягає в тому, що критерій оптимальності залежить від елементів розв’язку, а умова функціонування об’єкту записується у вигляді лінійних рівнянь або нерівностей.