8. Алгоритм розрахунку повного факторного експерименту для випадку рівномірного числа паралельних дослідів

1) Для кожної стрічки матриці планування за формулою

,

де n – кількість паралельних дослідів, u – номер паралельного досліду, розраховують середнє арифметичне значення параметра оптимізації

2) З метою оцінки відхилення функції відгуку від його середнього значення за формулою

визначають дисперсію кожної стрічки матриці планування.

3) Перевіряють однорідність дисперсій за формулою ,

де: G_T – теоретичний критерій Кохрена, визначається з додатків; m=N; f=N(n-1);

G_P – розрахунковий критерій Кохрена, який визначається за формулою

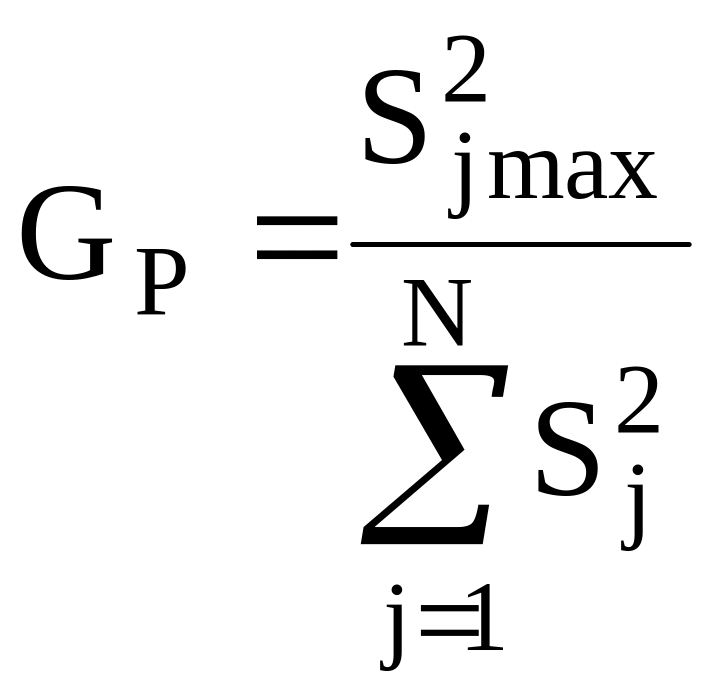
Гіпотеза приймається, якщо розрахунковий критерій Кохрена менший від теоретичного.

4) Визначають значення коефіцієнтів регресії за формулами

, , , ,

де і, k, u – номера факторів, x_ij, x_kj, x_uj – кодовані значення факторів в j-му досліді.

5) Перевіряють статичну значимість коефіцієнтів моделі за допомогою критерію Стьюдента t за формулою , де:

t_T – теоретичний критерій Стьюдента, який визначається з додатків, f=N(n-1);

t_p – критерій Стьюдента, розрахований за формулою ,

m – індекс коефіцієнта.

6) Обчислюють теоретичні значення функції ŷ_j за формулою

, відкинувши коефіцієнти, менші за t_T.

7) Визначають адекватність отриманої регресивної моделі за критерієм Фішера , де: F_T – теоретичне значення, яке вибирається з додатків, f₁=N(n-1), f₂=N–P; а F_p – за формулою

,

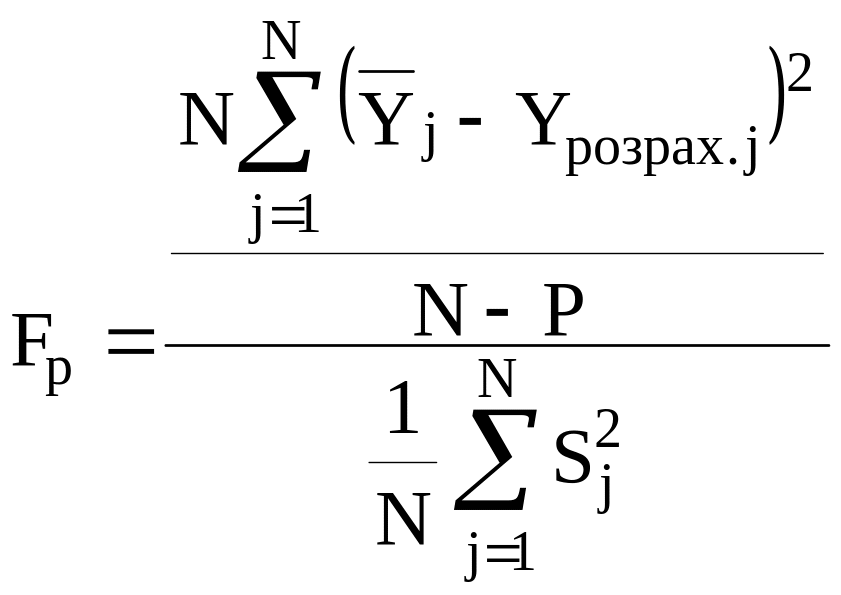де Р – число значущих коефіцієнтів математичної моделі.

Модель вважається адекватною, якщо розрахований критерій Фішера менший від теоретичного.

8) На основі отриманих коефіцієнтів будується регресійна модель у натуральних координатах.

Лекція 2 Методи статистичної оптимізації об’єктів керування

Розв’язок задачі оптимізації здійснюється в два етапи:

- пошуки в області екстремуму;

- уточнення екстремальної точки за допомогою додаткових пошукових дослідів або за допомогою математичної моделі.

Методи поділяються на класичні і факторні.

1. Класичні методи визначення екстремуму

За класичними методами пошукові досліди ставляться шляхом почергового варіювання незалежних змінних. На цей час всі інші фактори фіксуються.

Метод Гауса-Зейделя

Якщо , то рухаємося в напрямі К₀ – К₂

Закінчення процедури, якщо для будь-яких трьох точок Х_m-1, X_m, X_m+1 виконується

Y(X_m-1,1)<Y(X_m,1)<Y(X_m+1,1)  K_m відповідає локальному екстремуму. У нашому випадку – це точка К₃

На другому етапі за базову точку вибирається точка екстремуму, наприклад К₃, і процедура продовжується

Перевага: простота, наглядність;

Недоліки: трудність стабілізації керованих факторів, що зумовлює додаткові похибки у знаходженні часткових екстремумів.

Градієнтний метод

Ряд Тейлора в околі точки х₀

Суть методу полягає в тому, що на кожному етапі руху до екстремуму біля вибраної базової точки здійснюють пробні досліди, які дозволяють вибрати напрям градієнта і вибирається робочий крок λ. Такий рух дозволяє вибрати нову точку, яка наближує нас до екстремуму.

Наступна точка вибирається з умови:

Напрям градієнта К₀К₅ будується так, щоб для вибраного λ

; .

Для цього отримують λА₁ і λА₂. Отримані значення відкладаються від базової точки К₀ вздовж осей х₁ і х₂. Таким чином, отримують координати нової точки К₅ і повторюють алгоритм.

Алгоритм продовжується до тих пір, поки усі величини А_j будуть нескінченно малі.

Існують різні модифікації градієнтних методів, які відрізняються правилом вибору кроку λ.

Приклад. Знайти максимум функції .

Знаходимо

Вибираємо початкову точку

та знаходимо значення функції в цій точці

Нехай λ=0,1=const. Тоді

.

Знаходимо наступну точку за формулою :

; та знаходимо значення функції в цій точці

На другій ітерації отримуємо

;

Знаходимо .

Модифікований градієнтний метод

Знайти екстремум (максимум) функції

Вибираємо початкову точку

та знаходимо значення функції в цій точці

Знаходимо наступну точку

Складаємо вираз для приросту цільової функції на першому кроці

Знайдемо λ, для якого цей приріст є максимальний

Тоді

Значення функції

На другому кроці

Значення функції