Задание 181–185. На графике функции найти точку, в которой касательная к графику параллельна прямой .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
|
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
.
Задание 186–190. На
графике функции
найти точку, в которой касательная к
графику перпендикулярна прямой
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
, |
|
|
|
|
|
|
|
|
,
,
,
.
,
,
,
.
,
,
,
,
,
.
,
,
,
.
Задание 191–210. Исследовать данные функции методами дифференциального исчисления и начертить их графики. Исследование и построение графика рекомендуется проводить по следующей схеме: 1) найти область существования функции; 2) исследовать функцию на непрерывность; найти точки разрыва функции и её односторонние пределы в точках разрыва; 3) выяснить, не является ли данная функция четной, нечетной; 4) найти точки экстремума функции и определить интервалы возрастания и убывания функции; 5) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции; 6) найти асимптоты графика функции, если они имеются; 7) построить график функции, используя результаты исследования; при необходимости можно дополнительно находить точки графика, давая аргументу х ряд значений и вычисляя соответствующие значения у.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 211–220.
Требуется изготовить из жести ведро без крышки данного объема
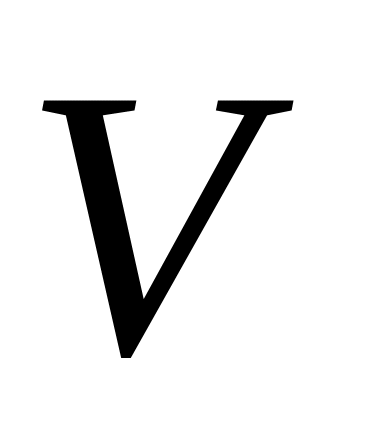цилиндрической формы. Каковы должны
быть высота цилиндра и радиус его
основания, чтобы на изготовление ведра
ушло наименьшее количество материала?Равнобедренный треугольник, вписанный в окружность радиусом
,
вращается вокруг прямой, проходящей
через его вершину параллельно основанию.
Какова должна быть высота этого
треугольника, чтобы тело, полученное
в результате его вращения, имело
наибольший объем?Прямоугольник вписан в эллипс с осями
и
.
Каковы должны быть стороны прямоугольника,
чтобы его площадь была наибольшей?Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом .
Найти радиус основания и высоту конуса наименьшего объема, описанного около шара радиусом .
При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность?
Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен а. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света?
Требуется изготовить закрытый цилиндрический бак максимальной вместимости. Каковы должны быть размеры бака (радиус
и высота Н), если на его изготовление
имеется S
= 18,84 м2
материала
?В прямоугольной системе координат через точку М (2; 3) проведена прямая, которая вместе с осями координат образует треугольник, расположенный в первом квадранте. Каковы должны быть отрезки, отсекаемые прямой на осях координат, чтобы площадь треугольника была наименьшей?
Резервуар, открытый сверху, имеет форму прямоугольного параллелепипеда с квадратным основанием. Каковы должны быть размеры резервуара, чтобы на его изготовление пошло наименьшее количество материала, если он должен вмещать 256 л воды?