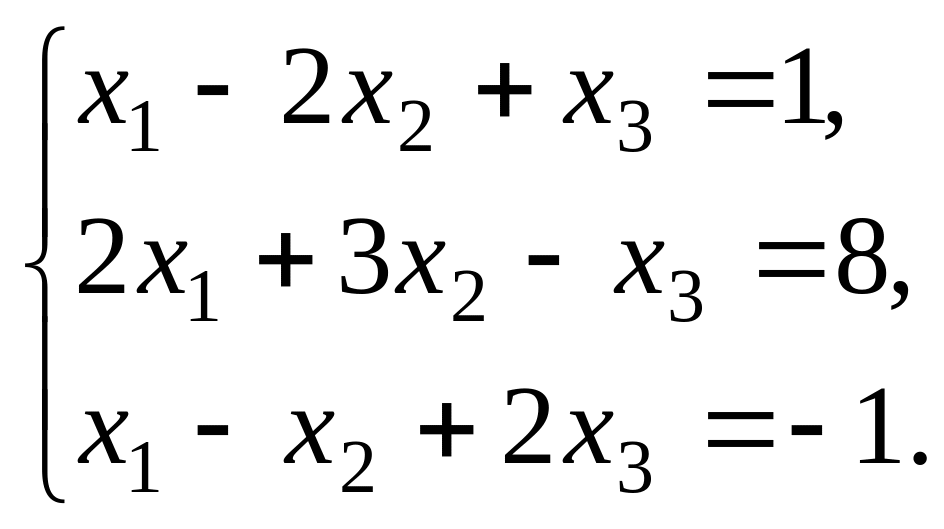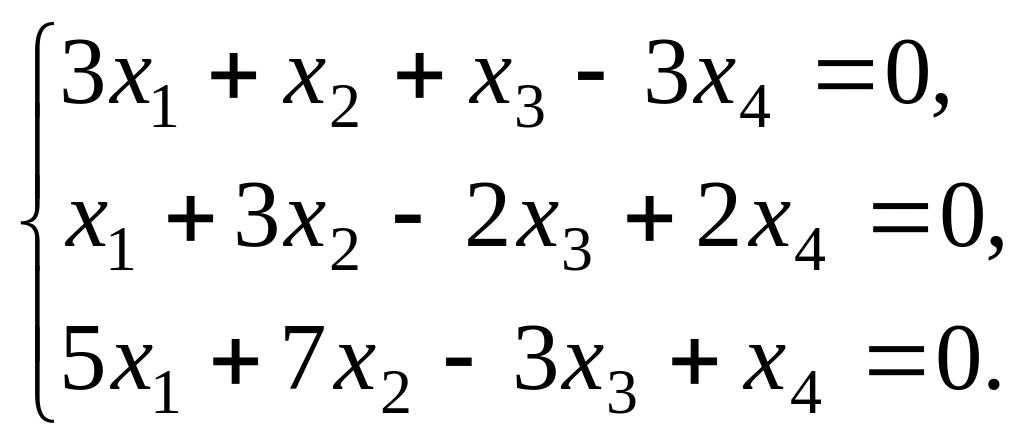Задания к контрольным работам

Задание 1–10. Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти её решение с помощью формул Крамера; 2) записать систему в матричной форме и решить её средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

Задание 11–20. В задачах данную систему уравнений решить методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы.

Задание 21–30. Найти множество решений однородной системы трех линейных уравнений с четырьмя неизвестными.

Задание 31–40. Исследовать данную систему уравнений на совместность и решить ее, если она совместна.

	38.

Задание 41–50. Даны векторы , , и в некотором базисе. Показать, что векторы образуют базис, и найти координаты вектора в этом базисе.

	,	,	,	.
	,	,	,	.

Задание 51–60. В задачах 51-60 даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты CD и её длину; 5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой CD ; 6) уравнение прямой, проходящей через точку К параллельно стороне АВ; 7) координаты точки М, расположенной симметрично точке А относительно прямой CD.

	,	,	.
	,	,	.
	,	,	.
	,	,	.
	,	,	.
	,	,	.
	,	,	.
	,	,	.
	,	,	.
	,	,	.