3.2 Задания типа 11-20

Если каждому значению переменной х из множества Х по некоторому правилу поставлено в соответствие единственное вполне определенное значение y, то переменную y называют функцией от х.

Записывают или . Говорят ещё, что функция отображает множество Х на множество Y .

Множество Х называется областью определения функции и обозначается . Множество всех называется множеством значений функции и обозначается .

х – независимая переменная величина или аргумент, y – функция или зависимая переменная.

Число А называется пределом функции при , если для любого положительного числа найдется такое положительное число , что для всех , удовлетворяющих неравенству , выполняется неравенство . Записывают .

Аналогично:

, если при , N – произвольное положительное число.

, если при , где М – произвольное сколько угодно большое положительное число. В этом случае функция называется бесконечно большой величиной при .

Если , то функция называется бесконечно малой величиной при .

Простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0

.

Практическое вычисление пределов основывается на следующих теоремах.

Если существуют конечные и , то

1)

2)

3) (с – константа)

4) , ( ).

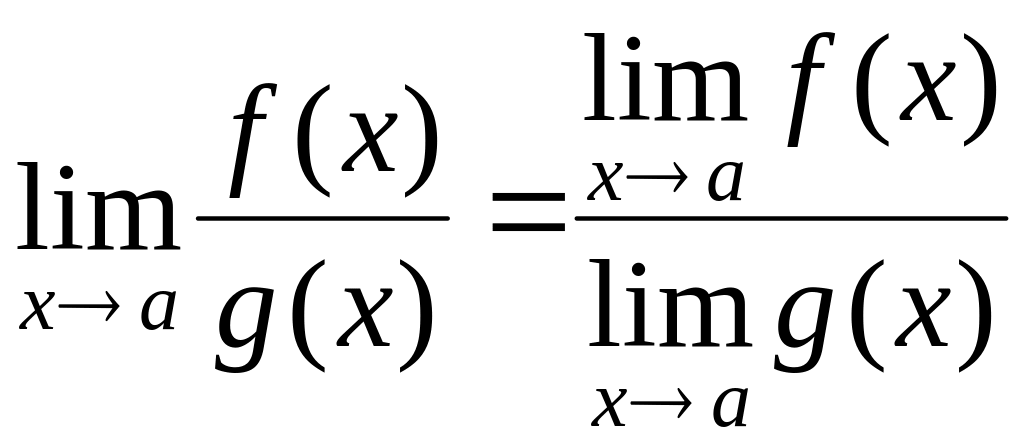Используются также следующие пределы:

; - первый замечательный предел;

; - второй замечательный предел. Число е≈2,71828.

С числом е связана система логарифмов, более удобная, чем десятичная.

- называется натуральный логарифм.

Число е называют ещё неперовым числом (по имени одного из первых изобретателей логарифмических таблиц Непера (1550-1617)). Показательная функция играет большую роль при изучении различных явлений в механике (теория колебаний), в электротехнике, радиотехнике. Функцию часто называют экспонентой и обозначают .

Разберем подобные примеры из контрольной работы. Найти пределы, не пользуясь правилом Лопиталя:

а) б)

Обычно для отыскания предела используют теоремы о пределах. Из этих теорем следует: если предельная точка входит в область определения функции, стоящей под знаком предела, то для его отыскания нужно найти значение функции в этой точке.

.

Но часто теоремы о пределах применить нельзя. Это бывает в случаях, так называемых, неопределенных выражений: .

Рассмотрим основные способы раскрытия неопределенностей на указанных выше примерах.

а)

Решение. Теорему о пределе частного применять нельзя, т.к. числитель и знаменатель неограниченно возрастают при . Имеем неопределенность вида . В подобных примерах числитель и знаменатель дроби целесообразно разделить на высшую степень переменной. В нашем примере разделим числитель и знаменатель на , затем перейдем к пределу.

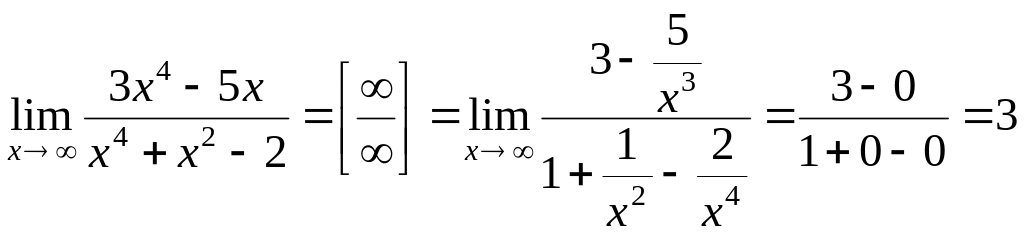
б)

Решение. Подставляя х=2 в числитель и знаменатель дроби получим неопределенность вида . В подобных примерах, когда числитель и знаменатель многочлены, их необходимо разложить на множители, после этого дробь сократить и прейти к пределу. Для разложения на множители квадратного трехчлена используем формулу , где х₁ ,х₂ – корни соответствующего квадратного уравнения

.