1. Встановити, чи зупиниться коли-небудь ця машина, якщо вона починає свою роботу із заданого слова (в початковий момент, в стані , машина знаходиться в комірці, в якій записана перша зліва буква слова, що переробляється).

2. У разі якщо машина зупиняється, визначити яке слово отримано нею в результаті, та яка її остання конфігурація.

14. Побудувати машину Тьюринга для обчислення заданої частково-числової функції. Прокоментувати вибір зовнішнього алфавіту та початкової конфігурації. Пояснити сенс кожного стану та переходу.

15. Елементи нескінченної таблиці нумеруються так, як вказано на рисунку. Знайти по заданому k його місце у таблиці i, j.

16. Задано вираз з арифметичними діями у вигляді стрічки. Визначити значення виразу. Врахувати наявність дужок.

17. У текстовому файлі збережено лабіринт. Написати програму виходу з лабіринту.

Варіант 4

1. Поняття повного набору логічних з’єднань. Теорема про повні набори логічних з’єднань. Приклади наборів, що не є повними.

2. Похідні правила виведення: теорема про правила введення логічних з’єднань.

3. Доведіть, що дана формула є теоремою числення висловлень, побудувавши послідовність формул, що є виводом даної формули із аксіом:

4. Доведіть, що в численні висловлень має місце наступна виводимість, побудувавши відповідне виведення із гіпотез:

5. Використовуючи теорему дедукції, доведіть, що наступна формула є теоремою числення висловлень:

6. Логічні операції над предикатами. Теорема про кон’юнкцію двох предикатів. Наслідки.

7. Записати наступне висловлювання за допомогою кванторів (на мові логіки предикатів) та за допомогою формул формалізованого числення предикатів. Для цього ввести необхідні предикати, предикатні та функціональні букви та терми:

Якщо кожен розумний філософ – цинік і тільки жінки є філософами, то тоді, якщо існують розумні філософи, то деякі з жінок – циніки.

8. Встановити, чи є терм вільним для змінної у формулі :

є , є

9. Нехай задано інтерпретацію:

, , ,

Вказати для яких значень змінних формула буде істинною в заданій інтерпретації:

є

10. Нехай задано інтерпретацію:

, , , ,

Обчислити значення функцій в заданій інтерпретації:

,

11. Концепція алгоритму. Нормальний алгоритм Маркова. Схема підстановок.

12. Побудувати нормальний алгоритм Маркова для обчислення наступної частково-числової функції. Прокоментувати вибір алфавіту, вказати призначення кожної з підстановок та продемонструвати роботу алгоритму на прикладі декількох вхідних слів в обраному алфавіті.

13. Задана машина Тьюринга із зовнішнім алфавітом та наступною функціональною схемою:

1	Вхідне слово:

Необхідно:

1. Встановити, чи зупиниться коли-небудь ця машина, якщо вона починає свою роботу із заданого слова (в початковий момент, в стані , машина знаходиться в комірці, в якій записана перша зліва буква слова, що переробляється).

2. У разі якщо машина зупиняється, визначити яке слово отримано нею в результаті, та яка її остання конфігурація.

14. Побудувати машину Тьюринга для обчислення заданої частково-числової функції. Прокоментувати вибір зовнішнього алфавіту та початкової конфігурації. Пояснити сенс кожного стану та переходу.

15. Службовий автобус з "Фабрика меблів "НОВА" здійснює один рейс по встановленому маршруту і, у випадку наявності вільних місць, підбирає робітників, котрі чекають на зупинці та відвозить їх на фабрику. Автобус також може чекати на зупинці робітників, які ще не прийшли. Відомо час приходу кожного робітника на свою зупинку і час проїзду автобуса від кожної зупинки до наступної. Автобус приходить на першу зупинку в нульовий момент часу. Тривалість посадки робітників в автобус вважаємо нульовою. Написати програму, яка визначить мінімальний час, за який автобус привезе максимально можливу кількість робітників.

16. Написати гру-стрілялку розстрілювання рухомої мішені. Враховувати кут польоту та силу.

17. Гра Ґранді (Ґвідо Ґранді (1671-1742) — італійський математик). На початку гри є одна загальна група предметів, що містить n предметів. Два гравці по черзі розбивають одну з наявних \grup на дві нерівні частини. Гра триває доти, доки всі групи не міститимуть 1-2 предмети. Переможцем вважають того, хто виконає останнє розбиття. Гру реалізувати з комп’ютером

Варіант 5

1. Числення висловлювань. Аксіоми. Поняття виводу. Правило виводу MP.

2. Похідні правила виведення: теорема про правила видалення логічних з’єднань.

3. Доведіть, що дана формула є теоремою числення висловлень, побудувавши послідовність формул, що є виводом даної формули із аксіом:

4. Доведіть, що в численні висловлень має місце наступна виводимість, побудувавши відповідне виведення із гіпотез:

5. Використовуючи теорему дедукції, доведіть, що наступна формула є теоремою числення висловлень:

6. Логічні операції над предикатами. Теорема про диз’юнкцію двох предикатів. Наслідки.

7. Записати наступне висловлювання за допомогою кванторів (на мові логіки предикатів) та за допомогою формул формалізованого числення предикатів. Для цього ввести необхідні предикати, предикатні та функціональні букви та терми:

Послідовність має границю.

8. Встановити, чи є терм вільним для змінної у формулі :

є , є

9. Нехай задано інтерпретацію:

, , ,

Вказати для яких значень змінних формула буде істинною в заданій інтерпретації:

є

10. Нехай задано інтерпретацію:

, , , ,

Обчислити значення функцій в заданій інтерпретації:

,

11. Машина Тьюринга. Схема будови та принцип роботи. Поняття конфігурації та стандартної конфігурації.

12. Побудувати нормальний алгоритм Маркова для обчислення наступної частково-числової функції. Прокоментувати вибір алфавіту, вказати призначення кожної з підстановок та продемонструвати роботу алгоритму на прикладі декількох вхідних слів в обраному алфавіті.

13. Задана машина Тьюринга із зовнішнім алфавітом та наступною функціональною схемою:

1	Вхідне слово:

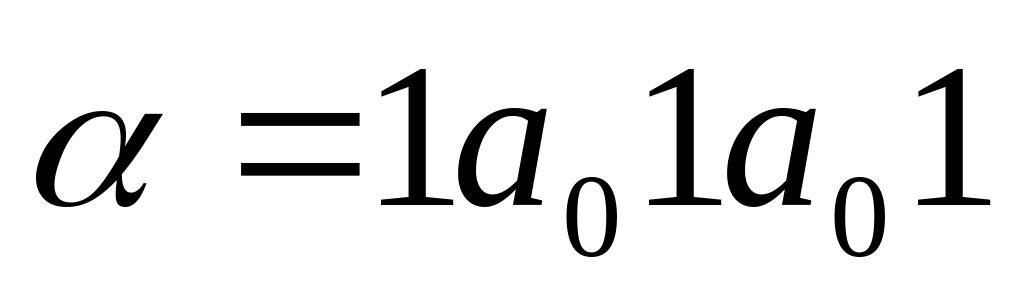
Необхідно: