Варіант 1

1. Висловлювання, пропозиційні букви та пропозиційні форми. Поняття тавтології. Приклади.

2. Похідні правила виведення: теорема про правила видалення логічних з’єднань.

3. Доведіть, що дана формула є теоремою числення висловлень, побудувавши послідовність формул, що є виводом даної формули із аксіом:

4. Доведіть, що в численні висловлень має місце наступна виводимість, побудувавши відповідне виведення із гіпотез:

5. Використовуючи теорему дедукції, доведіть, що наступна формула є теоремою числення висловлень:

6. Поняття предиката. Класифікація предикатів. Множина істинності предиката.

7. Записати наступне висловлювання за допомогою кванторів (на мові логіки предикатів) та за допомогою формул формалізованого числення предикатів. Для цього ввести необхідні предикати, предикатні та функціональні букви та терми:

Будь-яке натуральне число, що ділиться на 12, ділиться також на 2, 4 та 6

8. Встановити, чи є терм 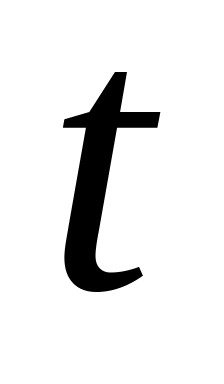вільним для змінно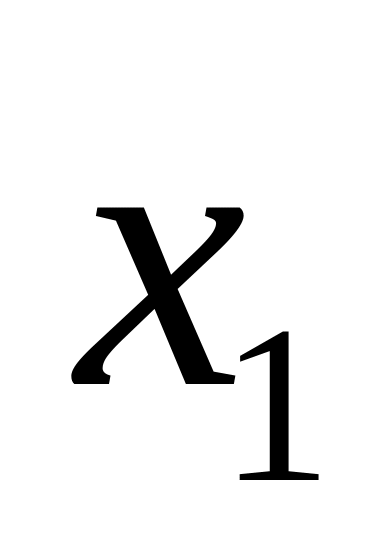ї у формулі :

є , є

9. Нехай задано інтерпретацію:

, , ,

Вказати для яких значень змінних формула буде істинною в заданій інтерпретації:

є

10. Нехай задано інтерпретацію:

, , , ,

Обчислити значення функцій в заданій інтерпретації:

,

11. Частково-числові функції. Операції суперпозиції та примітивної рекурсії. Приклади.

12. Побудувати нормальний алгоритм Маркова для обчислення наступної частково-числової функції. Прокоментувати вибір алфавіту, вказати призначення кожної з підстановок та продемонструвати роботу алгоритму на прикладі декількох вхідних слів в обраному алфавіті.

13. Задана машина Тьюринга із зовнішнім алфавітом 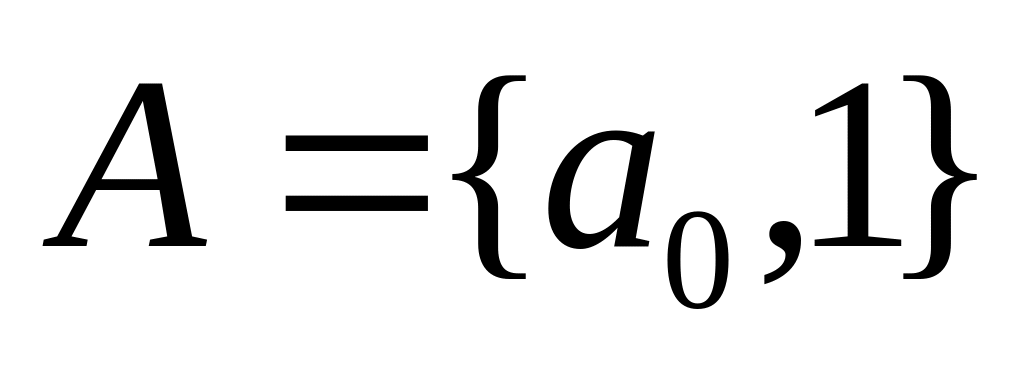та наступною функціональною схемою:

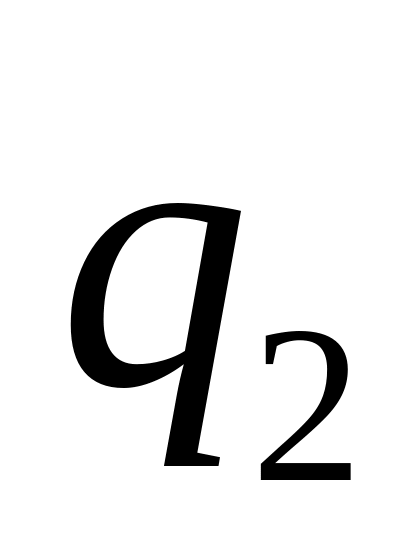
1	Вхідне слово:

Необхідно:

1. Встановити, чи зупиниться коли-небудь ця машина, якщо вона починає свою роботу із заданого слова (в початковий момент, в стані , машина знаходиться в комірці, в якій записана перша зліва буква слова, що переробляється).

2. У разі якщо машина зупиняється, визначити яке слово отримано нею в результаті, та яка її остання конфігурація.

14. Побудувати машину Тьюринга для обчислення заданої частково-числової функції. Прокоментувати вибір зовнішнього алфавіту та початкової конфігурації. Пояснити сенс кожного стану та переходу.

15. Написати гру 8-мірки: цифри від 1 до 8 задані у довільному порядку у вигляді масиву 3х3. один елемент - порожній. Завдання: впорядкувати цифри за зростанням, міняючи місцями цифру та порожній елемент. Рух по діагоналі заборонений. Половина балів – за надання можливості користувачеві самостійно переставляти фішки з відображення результатів на екран. Повна сума балів – за розставляння фішок комп’ютером.

16. Написати гру морський бій. Користувач задає свої кораблі, кораблі комп’ютера розставляються випадково, кораблі не доторкаються. Для стріляння комп’ютера запропонувати стратегію.

17. Написати гру «Змійка». Керування змією здійснюється за чотирма напрямами клавіатурою. Змія пересувається по робочому полі та з’їдає яблука. Від цього вона виростає на одну одиницю1. Гра завершується, якщо змія будь-якою частиною тіла доторкнеться до краю поля або самої себе.

Варіант 2

1. Поняття тавтології. Леми про тавтології.

2. Похідні правила виведення: теорема про правила введення логічних з’єднань.

3. Доведіть, що дана формула є теоремою числення висловлень, побудувавши послідовність формул, що є виводом даної формули із аксіом:

4. Доведіть, що в численні висловлень має місце наступна виводимість, побудувавши відповідне виведення із гіпотез:

5. Використовуючи теорему дедукції, доведіть, що наступна формула є теоремою числення висловлень:

6. Рівносильні предикати та предикати, що є випливають з інших предикатів. Теореми.

7. Записати наступне висловлювання за допомогою кванторів (на мові логіки предикатів) та за допомогою формул формалізованого числення предикатів. Для цього ввести необхідні предикати, предикатні та функціональні букви та терми:

Мешканці Швейцарії обов’язково володіють або французькою, або італійською або німецькою мовою.