Московский университет имени С.Ю. Витте, Парфенова М.Я

Тема 2. Алгебра логики

Аппарат алгебры логики был создан с целью изучения логики мышления математическими методами. Основателем логики как науки считается Аристотель (384-322г. до нашей эры). Он систематизировал известные до него знания, и эта система знаний называется сейчас формальной логикой. Дальнейшее развитие логики связано с именем немецкого математика Г. Лейбница (1646-1716 г.). Он предложил конструктивную модель построения логики. Его идея состоит в разложении того или иного понятия на составляющие, которые должны быть обозначены символами. Каждому основному понятию должен соответствовать символ. Сложные понятия должны строиться из основных (символов), которые соединяются по особым правилам. Лейбницу не удалось реализовать свою идею. Её реализовал английский учёный Джордж Буль (1815-1864 г.), основные положения которой опубликовал в 1854 г. Он ввёл символьное обозначение для высказываний и создал алгебру высказываний. В такой форме логика получила название математической логики.

Аппарат алгебры логики (альтернативное название “булевой алгебры”), впервые на практике применил Клод Шеннон для создания релейных переключательных сетей в 1938 г.

Основное понятие алгебры логики — выказывание. Под простым высказыванием понимается повествовательное предложение, о котором можно сказать, истинно оно или ложно (третьего не дано). Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: 1) ЛОЖЬ (false - f ), которое обозначим как 0 (ноль); 2) ИСТИНА (true – t), которое обозначим 1. Например, содержание высказывания А «дважды два равно четырем» истинно, т.е. А = 1; а высказывание В «три больше пяти» всегда есть ЛОЖЬ, т.е. В=0.

Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности, что записывается в виде А = В.

2.1. Логические операции

Рассмотрим основные логические операции, которые можно построить с использованием высказываний.

Сложное высказывание можно построить из простых высказываний с помощью следующих логических операций: отрицания, конъюнкции, дизъюнкции, импликации, эквивале́нции. Комбинации логических операций представляют собой логические выражения.

Операцией отрицания А называется высказывание “НЕ А” (обозначается А или ), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Описание этого правила можно представить в виде следующей таблицы, которая отражает возможные значения данной операции:

А
0	1
1	0

Такая таблица называется таблицей истинности.

Отрицание - это унарная логическая операция, т.е. выполняется с одним операндом. В вычислительных системах операции отрицания соответствует языковая конструкция, использующая частицу НЕ (NOT).

Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается С = А  В или С = А & В (при этом говорят С равно А и В). Например, чтобы снизить риск аварии необходимо знать правила дорожного движения и необходимо выполнять их. Данная операция применяется, если два высказывания связываются союзом И (AND).

Таблица истинности для этой операции имеет вид:

А	В	А  В
0	0	0
0	1	0
1	0	0
1	1	1

Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Операция записывается в виде С = A v В, читается “С равно А или В”. Например, высказывание А состоит в том, что «сотрудник может добираться домой на автобусе», событие В «сотрудник может добираться домой на троллейбусе», событие С «сотрудник добирается домой на автобусе ИЛИ троллейбусе». Данная операция применяется, если два высказывания связываются союзом ИЛИ (OR). Таблица истинности для этой операции имеет вид:

А	В	A v B
0	0	0
0	1	1
1	0	1
1	1	1

Импликацией (или условным высказыванием) двух высказываний А (А называется посылкой) и В (В называется заключением) является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно, записывается в виде С = А—>В, читается “С равно из А следует В” или “если А…, то В… “. Примером такой операции может быть любое рассуждение типа: если произошло событие А, то произойдет событие В, например, “если идет дождь, то на небе тучи”. Очевидно, что операция не симметрична, т.е. из В —> А не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно. Таблица истинности для операции импликации имеет вид:

А	В	А  В
0	0	1
0	1	1
1	0	0
1	1	1

Импликация имеет следующие свойства:

А  В  В  А

А  А = 1

1 А = А

А  1 = 1

А  0 =

Эквиваленцией (или биусловным высказыванием) двух высказываний А и В является новое высказывание С, которое истинно тогда и только тогда, когда оба высказывания имеют одинаковые значения истинности. Обозначается символом ↔ или ≡., записывается С = А↔ В (С = А ≡ В). Означает «A то же самое, что B», «A эквивалентно B», «A тогда и только тогда, когда B».. Таблица истинности для операции эквиваленции имеет вид:

А	В	А ↔ В
0	0	1
0	1	0
1	0	0
1	1	1

Эквиваленция имеет следующие свойства:

А↔ В=В↔ А

А↔ В=¬В↔ ¬А

А ↔ 1 =А

А ↔ 0 = ¬ А

Законы алгебры логики.

Логические операции, определённые на множестве, удовлетворяют следующим аксиомам, образующих алгебру логики:

1. - закон идемпотентности;

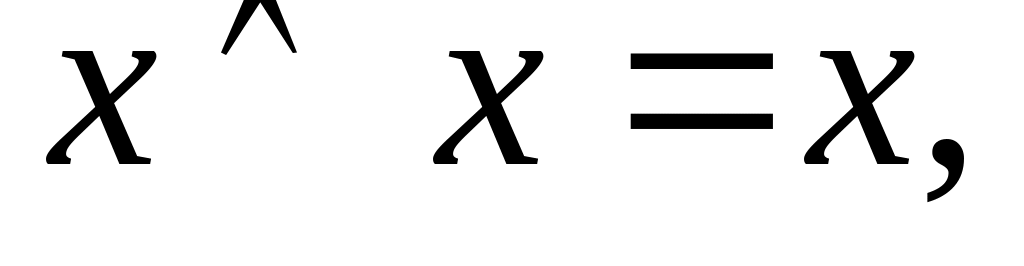
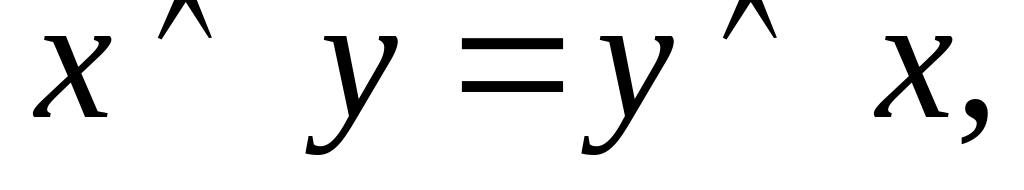
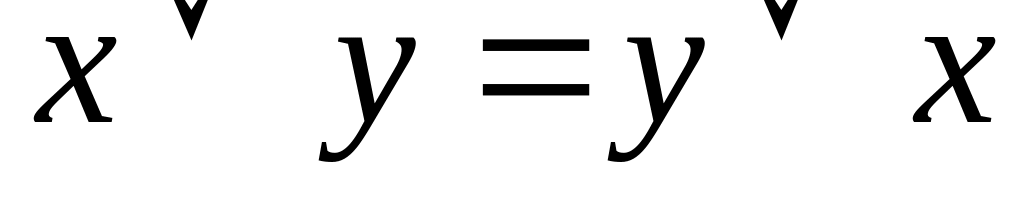2. - закон коммутативности;

3. - закон ассоциативности;

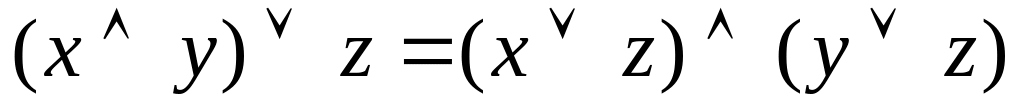4. - закон дистрибутивности;

5. - закон нуля и единицы;

6. - закон исключенного третьего и закон противоречия;

7. - закон поглощения;

8. - закон склеивания;

9. - закон де Моргана;

10. - закон двойного отрицания.

Все эти аксиомы подтверждаются непосредственной проверкой с помощью таблиц истинности для обеих сторон равенства.

Буквы, обозначающие высказывания, логические связки и скобки составляют алфавит логики высказываний. С помощью элементов алфавита можно построить разнообразные логические формулы. Например, высказывание А  В можно привести к логической формуле вида .