
- •Алгоритмы на графах
- •Обходы графов
- •Поиск в глубину (пг)
- •Алгоритм поиска в глубину в неориентированном связном графе
- •Поиск в ширину (пш)
- •Алгоритм поиска в ширину в неориентированном связном графе
- •Нахождение деревьев и остовов с помощью пг и пш
- •Нахождение дерева покрытия с помощью .
- •Нахождение дерева покрытия с помощью
- •Остов минимального веса (кратчайший остов)
- •Задача об остове минимального веса:
- •Алгоритм Краскала.
- •Алгоритм Прима.
- •Кратчайшие пути
- •Алгоритм Дейкстра
- •Алгоритм Дейкстра поиска кратчайшего пути.
- •Алгоритм Флойда
- •Алгоритм Флойда
Алгоритм Дейкстра поиска кратчайшего пути.
-
Положим
 и считать эту метку постоянной. Положим
и считать эту метку постоянной. Положим

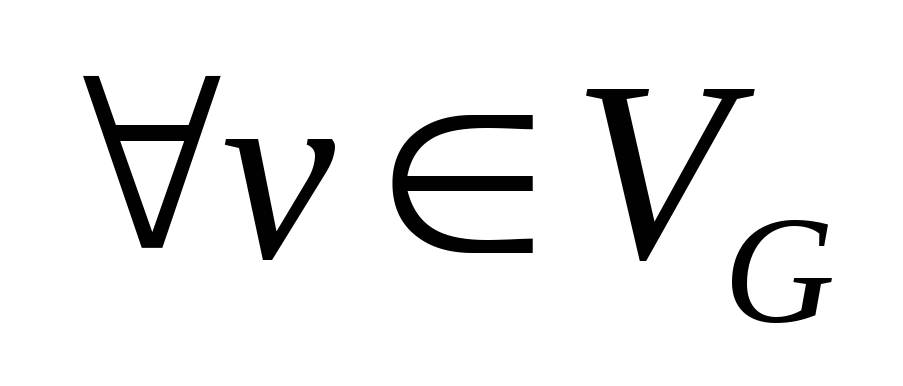 ,
,
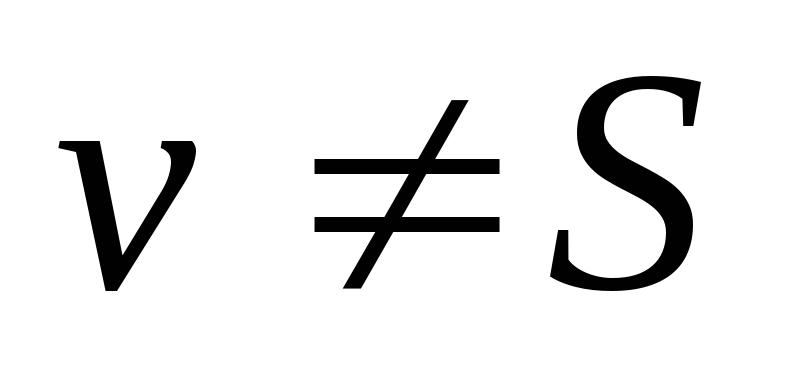 , и считая эти метки временными. Положить
, и считая эти метки временными. Положить
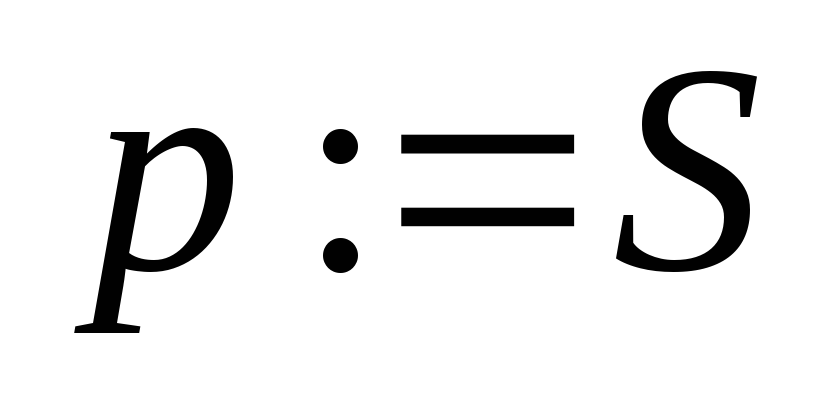 .
. -
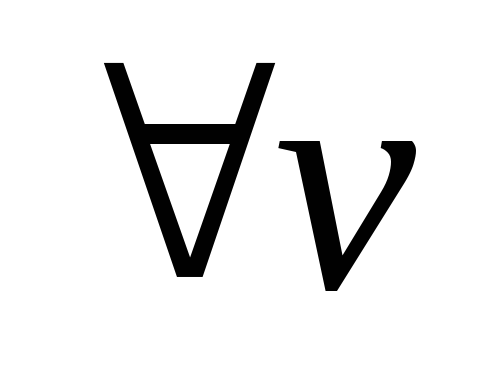 ,
выходящие из
,
выходящие из
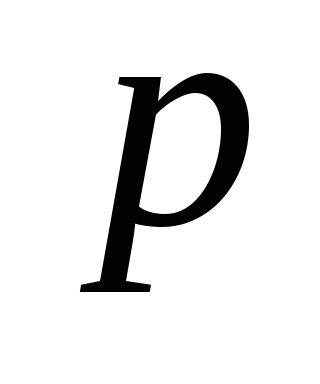 ,
с временными метками выполнить: если
,
с временными метками выполнить: если
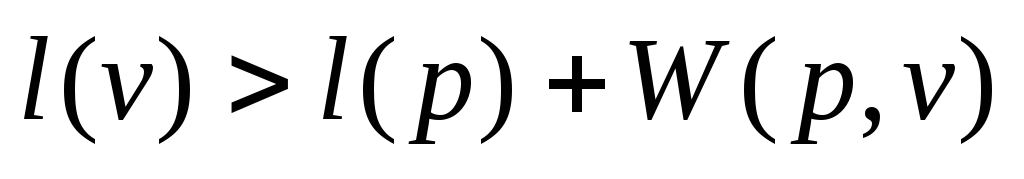 и
и
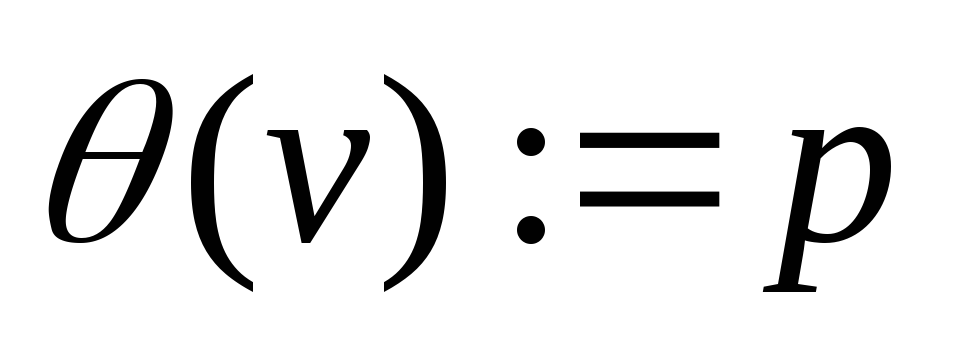 .
Иначе
.
Иначе
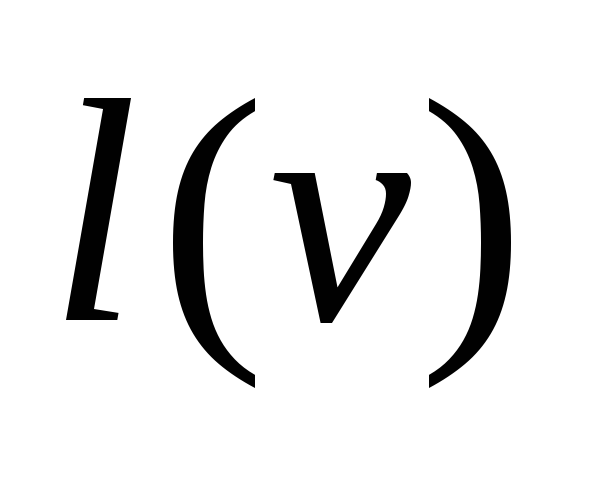 и
и
 не менять местами.
не менять местами. -
Пусть
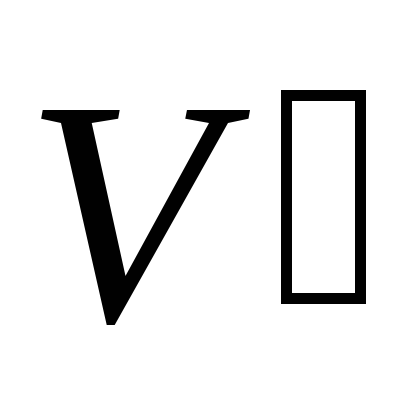 -
множество вершин с временными метками
-
множество вершин с временными метками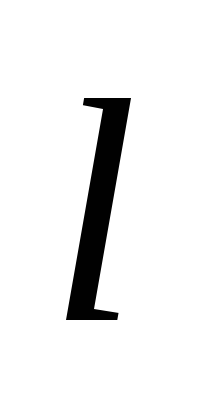 .
Найти вершину
.
Найти вершину
 такую что:
такую что:
![]()
Считать метку
![]() постоянной меткой вершины
постоянной меткой вершины
![]() .
.
-
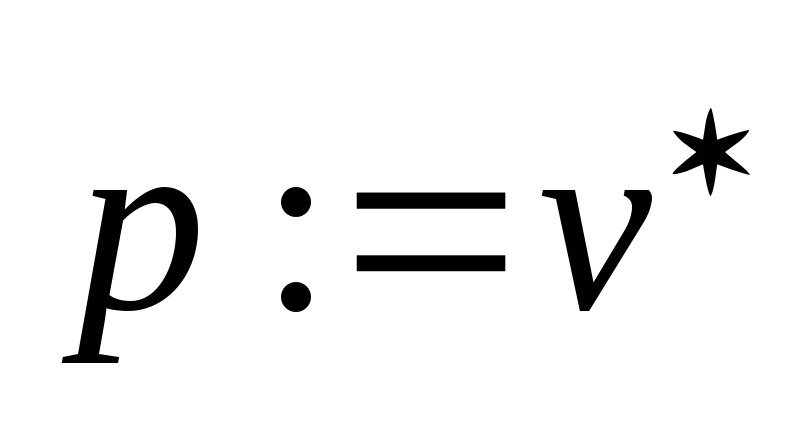 .
Если
.
Если
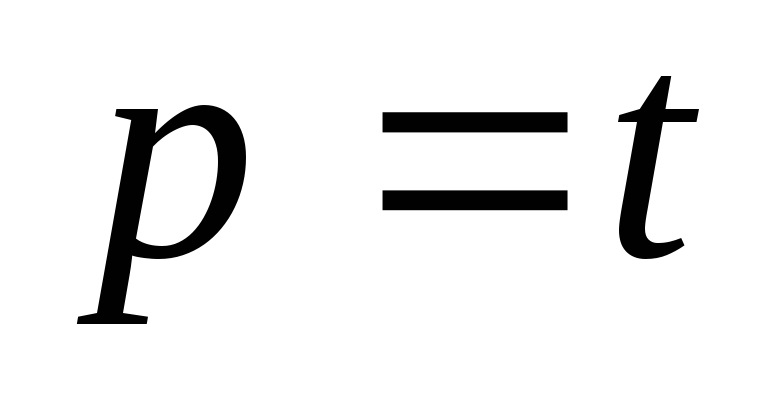 ,
то следовать п.5, где
,
то следовать п.5, где
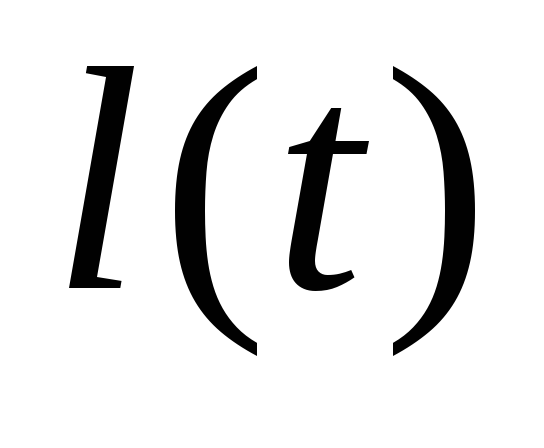 -
вес кратчайшего пути. Иначе перейти
п.2.
-
вес кратчайшего пути. Иначе перейти
п.2. -
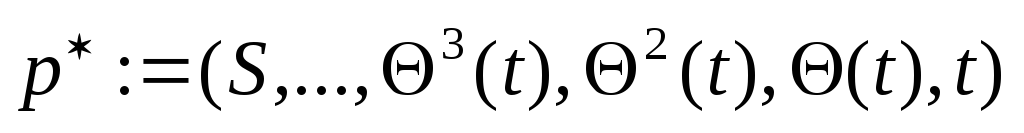 ,
где
,
где
 -кратчайший
путь. Конец.
-кратчайший
путь. Конец.
Замечание.
1). Алгоритм Дейкстры применим и к
неориентированным графам. Для этого
достаточно каждое неориентированное
ребро
![]() графа, имеющее вес
графа, имеющее вес
![]() ,
рассматривать как пару дуг
,
рассматривать как пару дуг
![]() и
и
![]() того же веса.
того же веса.
2). Если п.4. модифицировать так, чтобы
алгоритм заканчивал работу только после
получения всеми вершинами постоянных
меток, то он будет строить кратчайшие
пути из
![]() в каждую из остальных вершин. Если к
тому же вместе с превращением метки
вершины
в каждую из остальных вершин. Если к
тому же вместе с превращением метки
вершины
![]() в постоянную (п.3 алгоритма закосить
дугу
в постоянную (п.3 алгоритма закосить
дугу
![]() а множество
а множество
![]() ,
то после окончания работы алгоритма
граф
,
то после окончания работы алгоритма
граф
![]() будет корневым ориентированным остовным
деревом. Это дерево называют деревом
кратчайших путей из
будет корневым ориентированным остовным
деревом. Это дерево называют деревом
кратчайших путей из
![]() графа
графа
![]() .
Для любой вершины
.
Для любой вершины
![]() единственный
единственный
![]() -
путь в дереве
-
путь в дереве
![]() является кратчайшим
является кратчайшим
![]() - путь в графе
- путь в графе
![]() .
.
Алгоритм Дейкстры строится в графе
![]() кратчайший
кратчайший
![]() -путь
за время
-путь
за время
![]() .
.
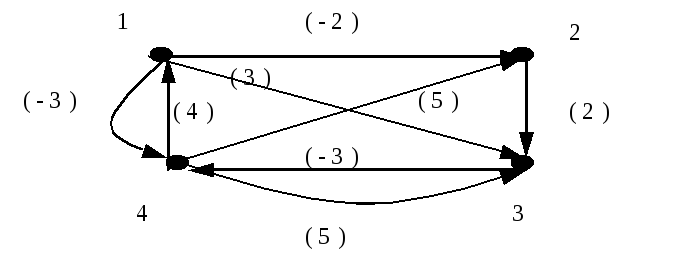
Построить дерево кратчайших путей из вершины 1 по алгоритму Дейкстры.
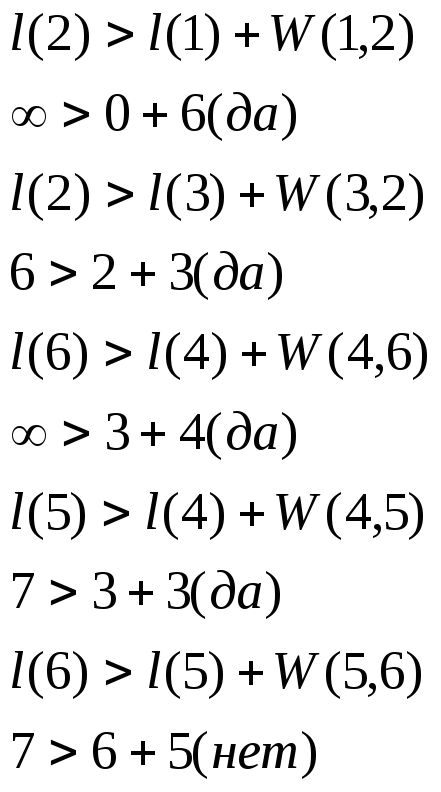

из2:
из3:
-
Алгоритм Флойда
Рассмотрим более общую ситуацию. Будем
считать, что в графе
![]() допускаются дуги отрицательного веса.
Опишем алгоритм нахождения кратчайших
путей между всеми парами вершин графа
при условии, что в графе нет отрицательных
контуров (замкнутых путей отрицательного
веса). Если же такой контур в графе есть,
то алгоритм сообщает об этом и прекращает
работу.
допускаются дуги отрицательного веса.
Опишем алгоритм нахождения кратчайших
путей между всеми парами вершин графа
при условии, что в графе нет отрицательных
контуров (замкнутых путей отрицательного
веса). Если же такой контур в графе есть,
то алгоритм сообщает об этом и прекращает
работу.
Будем считать, что граф
![]() задан матрицей весов дуг
задан матрицей весов дуг
![]() ,
,
-
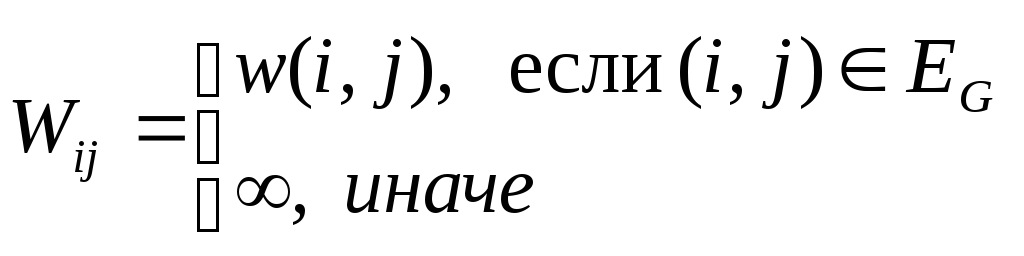 .
.
Кроме того, полагаем
![]() .
.
В алгоритме используются матрицы
![]() и
и
![]() .
Матрица
.
Матрица
![]() содержит веса кратчайших путей, проходящих
только через вершины
содержит веса кратчайших путей, проходящих
только через вершины
![]() .
.
-
В матрице
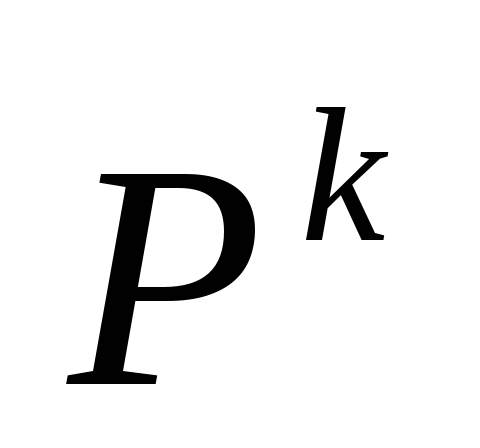
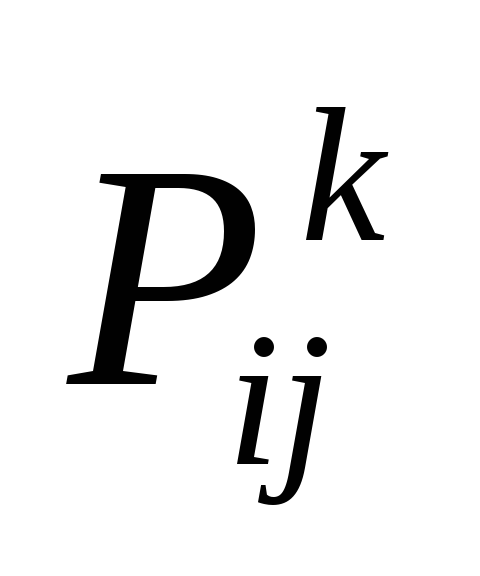 - номер вершины, предшествующий вершине
- номер вершины, предшествующий вершине
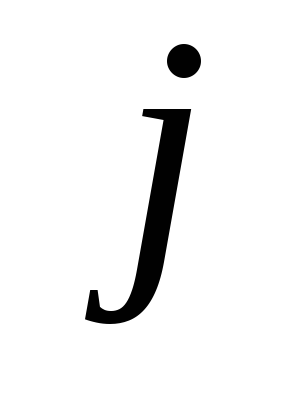 в текущем
в текущем
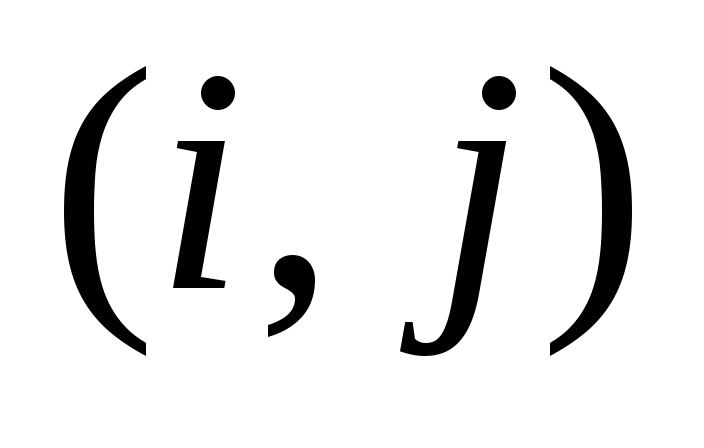 -пути.
Т.о., матрица
-пути.
Т.о., матрица
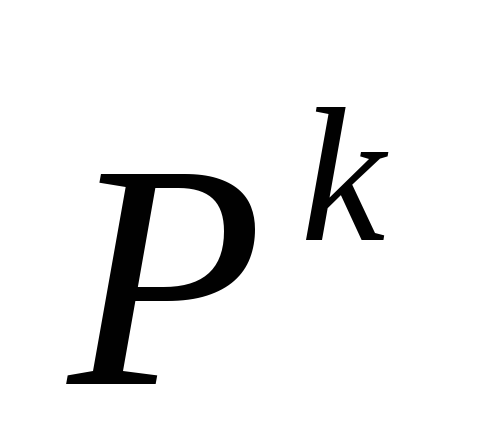 имеет тот же смысл, что и метка
имеет тот же смысл, что и метка
 в алгоритме Дейкстра.
в алгоритме Дейкстра.
Алгоритм Флойда
1).
![]() ;
;
![]() ;
;
![]() ,
,
-
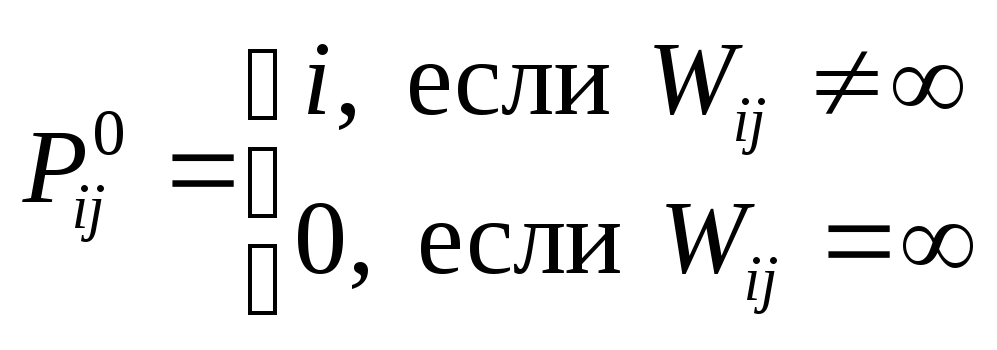 .
.
2).
![]() выполнить: если
выполнить: если
![]() ,
то
,
то
![]() ;
;
![]() .
Иначе
.
Иначе
![]() ;
;
![]() .
.
3). Если для некоторого
![]() ,
,
![]()
![]() ,
то конец (в графе имеется отрицательный
контур). Иначе перейти к п.4).
,
то конец (в графе имеется отрицательный
контур). Иначе перейти к п.4).
4).
![]() .
Если
.
Если
![]() ,
то конец (
,
то конец (![]() - матрица весов кратчайших путей,
определяемых с помощью матрицы
- матрица весов кратчайших путей,
определяемых с помощью матрицы
![]() ).
С помощью матрицы
).
С помощью матрицы
![]() кратчайший
кратчайший
![]() -путь
-путь
![]() определяется следующим образом:
определяется следующим образом:
![]() ,
,
![]()
Иначе перейти к п.2).
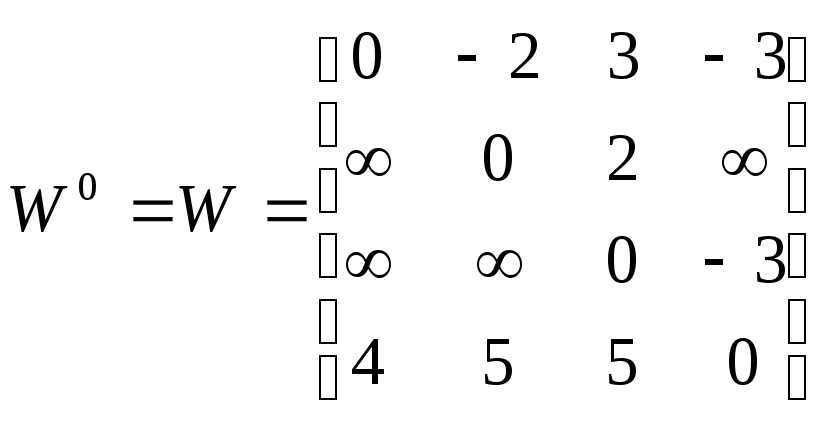 ,
,
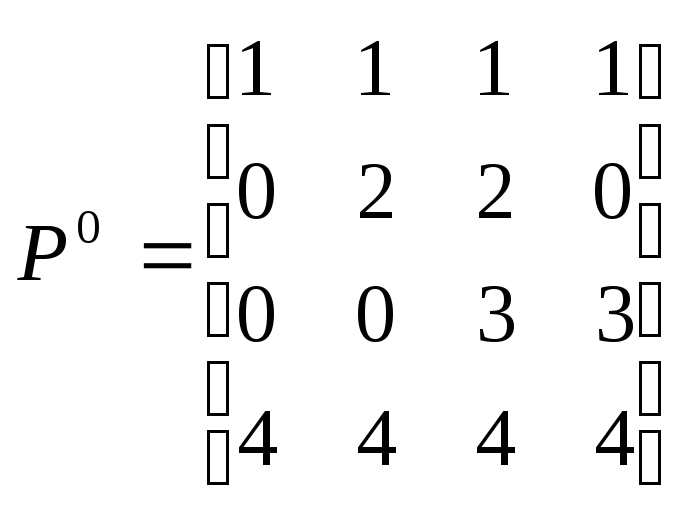
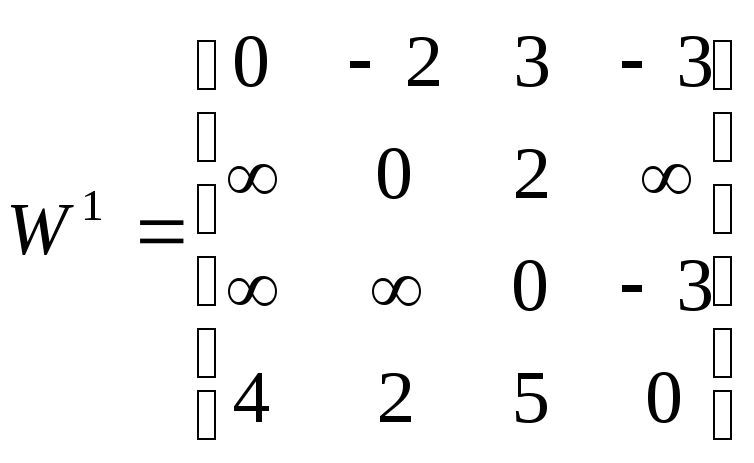 ,
,

 ,
,
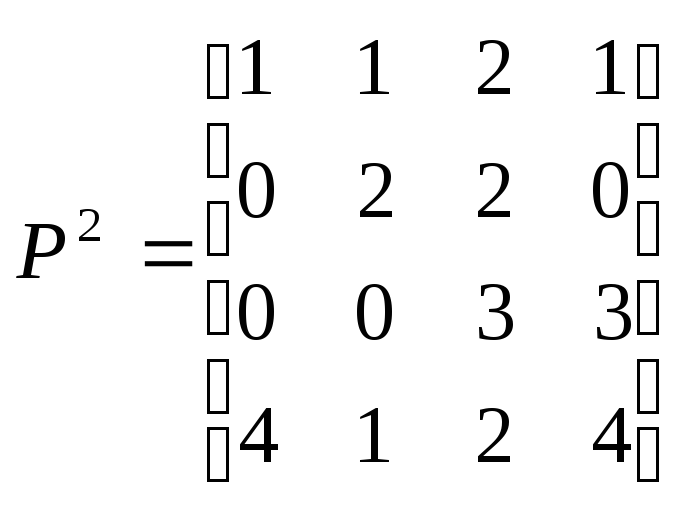
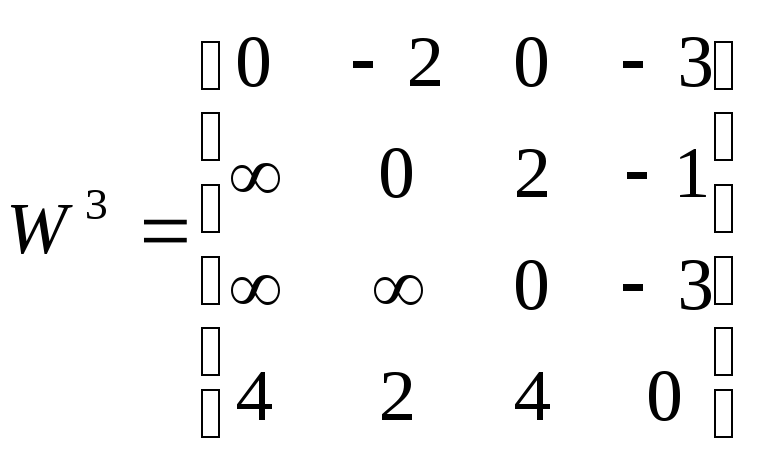 ,
,
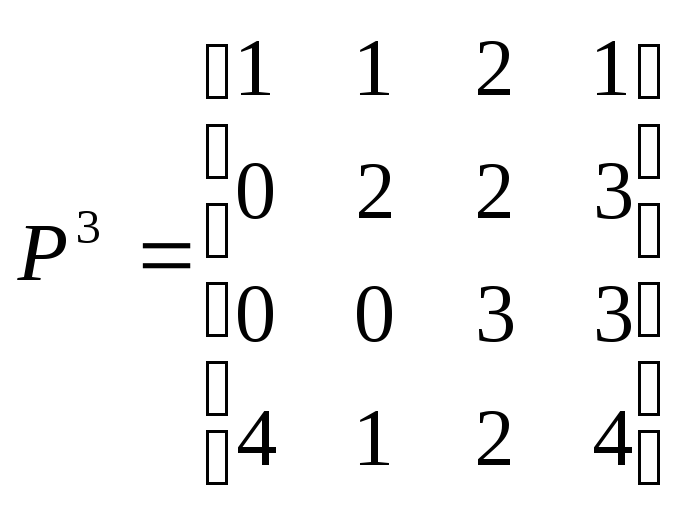
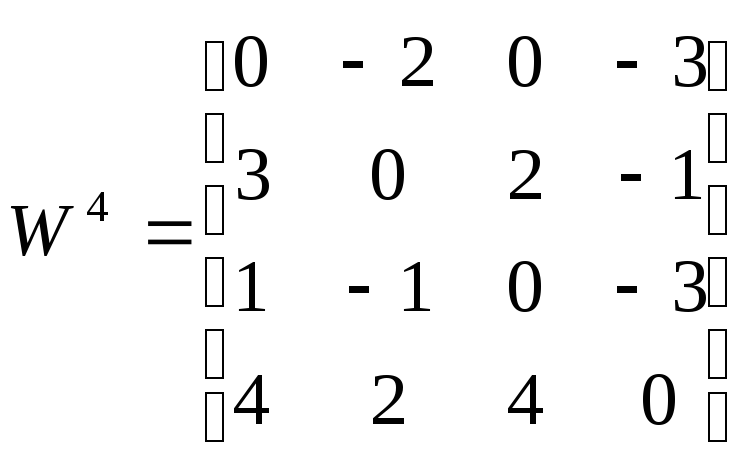 ,
,
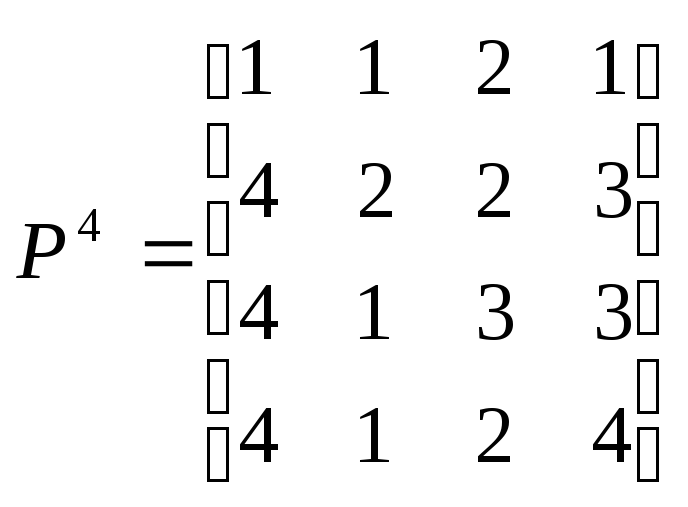
Найдем, например, с помощью матрицы
![]() кратчайший (2,1)-путь:
кратчайший (2,1)-путь:
![]() .
Длина этого пути
.
Длина этого пути
![]() .
.

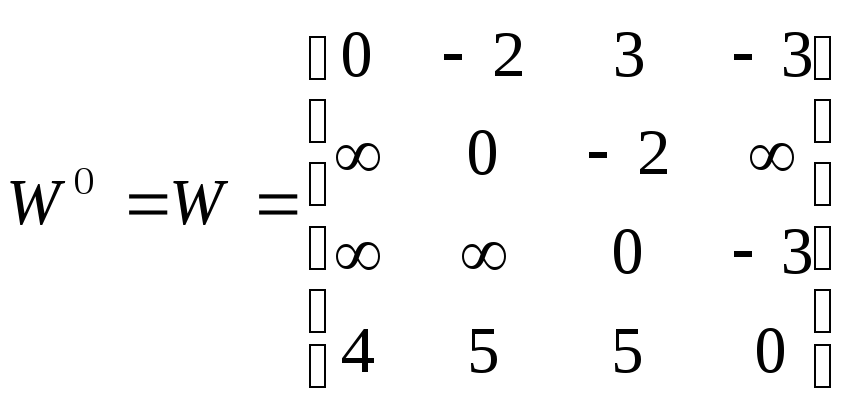 ,
,
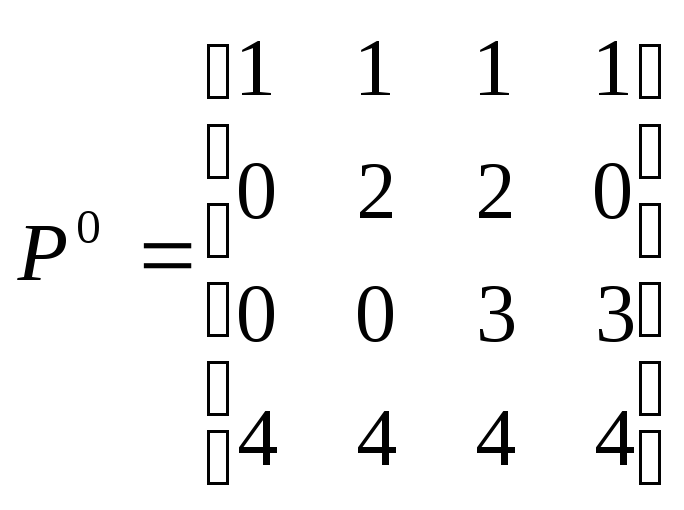
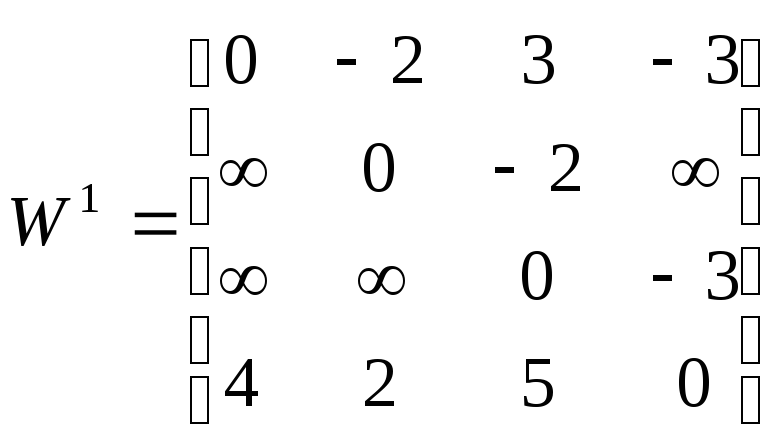 ,
,

 ,
,
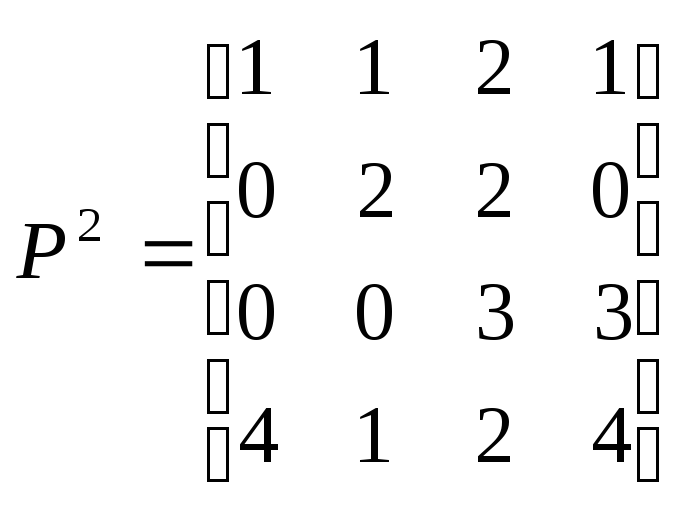
 ,
,
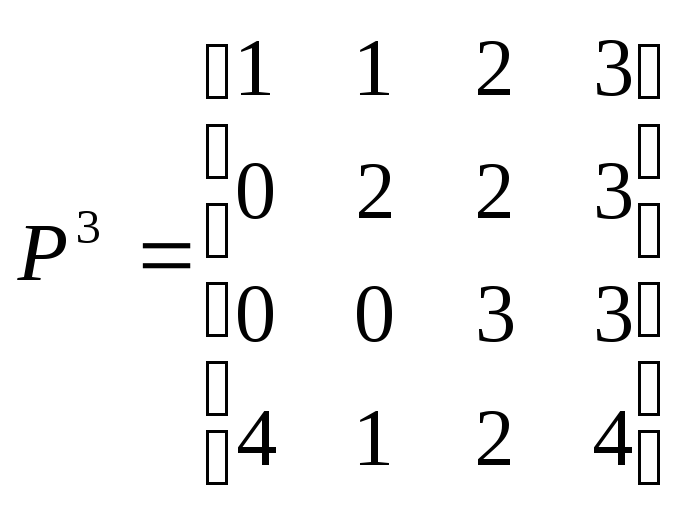
 ,
,
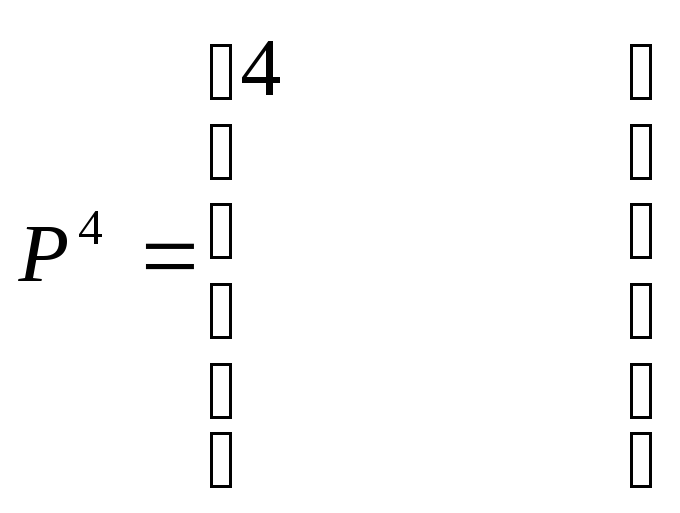
В графе есть контур отрицательного веса
(1,2,3,4),
![]() .
.
