
- •Алгоритмы на графах
- •Обходы графов
- •Поиск в глубину (пг)
- •Алгоритм поиска в глубину в неориентированном связном графе
- •Поиск в ширину (пш)
- •Алгоритм поиска в ширину в неориентированном связном графе
- •Нахождение деревьев и остовов с помощью пг и пш
- •Нахождение дерева покрытия с помощью .
- •Нахождение дерева покрытия с помощью
- •Остов минимального веса (кратчайший остов)
- •Задача об остове минимального веса:
- •Алгоритм Краскала.
- •Алгоритм Прима.
- •Кратчайшие пути
- •Алгоритм Дейкстра
- •Алгоритм Дейкстра поиска кратчайшего пути.
- •Алгоритм Флойда
- •Алгоритм Флойда
Нахождение дерева покрытия с помощью
Результат работы алгоритма – дерево
покрытия (ориентированное)
![]() .
Пусть
.
Пусть
![]() - вершина, с которой начинается поиск.
- вершина, с которой начинается поиск.
-
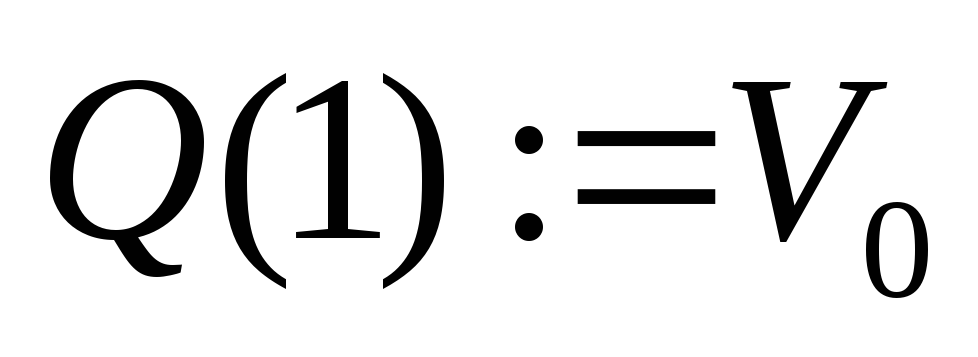 ;
;
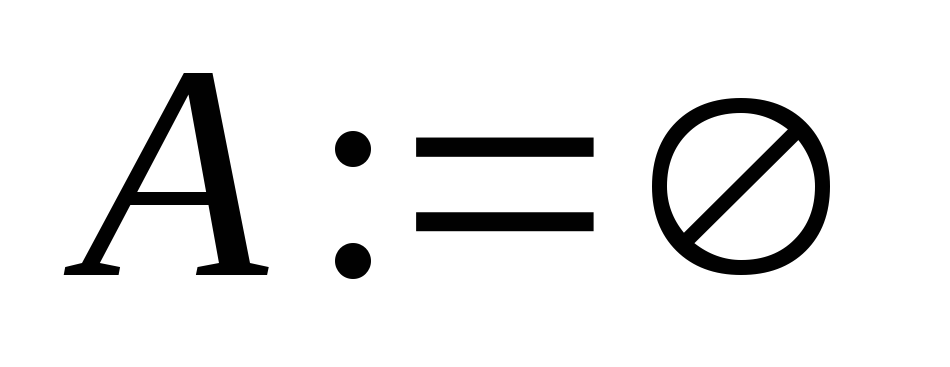 ;
;
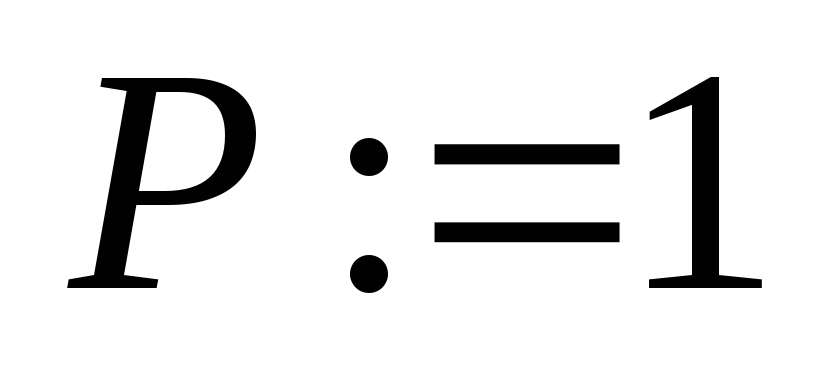 ;
// адрес 1-ой ячейки
;
// адрес 1-ой ячейки

![]() ;
// адрес последней ячейки
;
// адрес последней ячейки
![]()
-
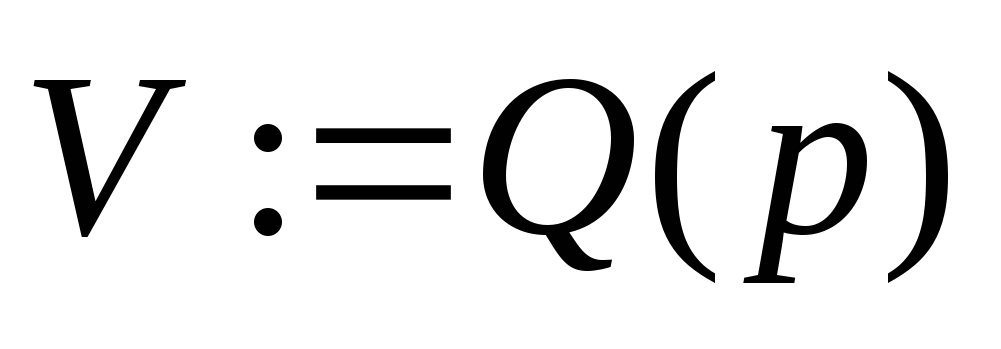 ;
;
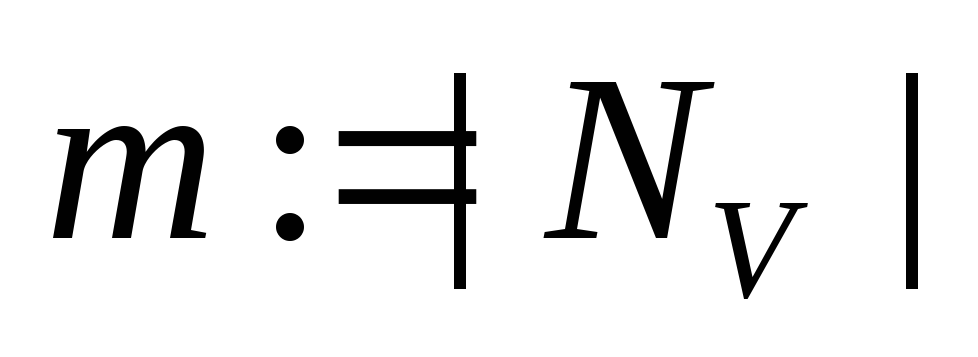 ;
; -
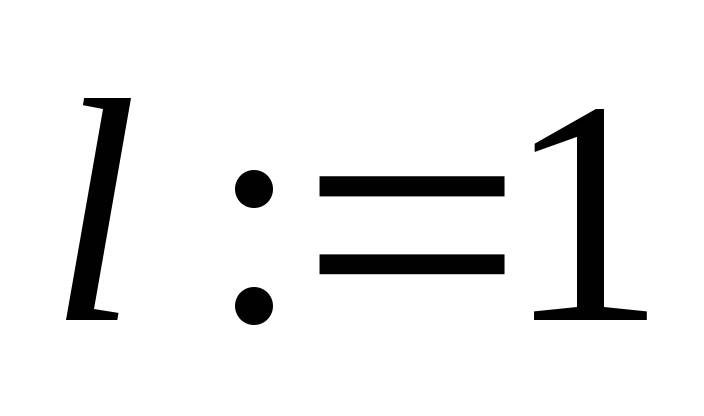 ;
; -
Если вершина
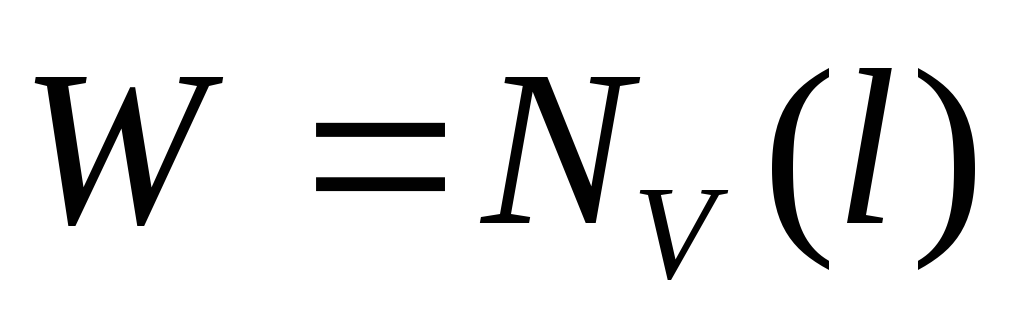 уже просмотрена, то
п.5. Иначе
уже просмотрена, то
п.5. Иначе
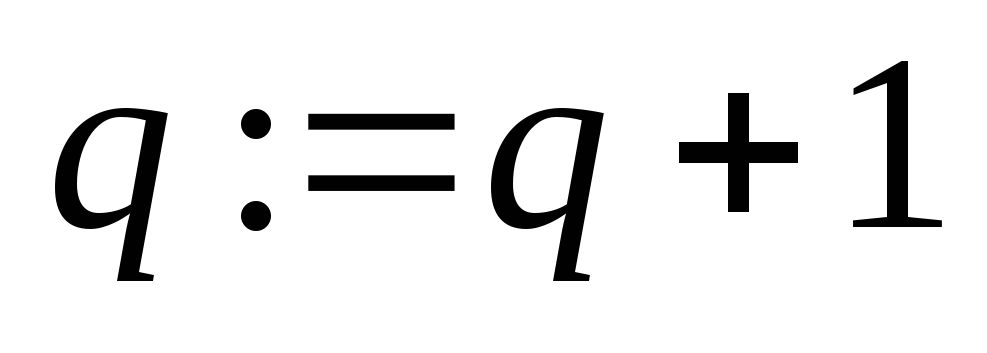 ;
;
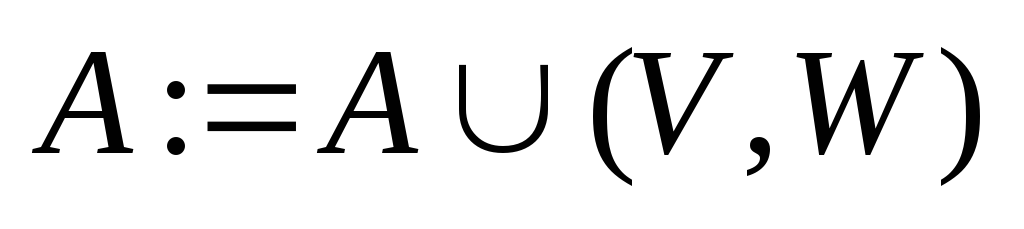 ;
;
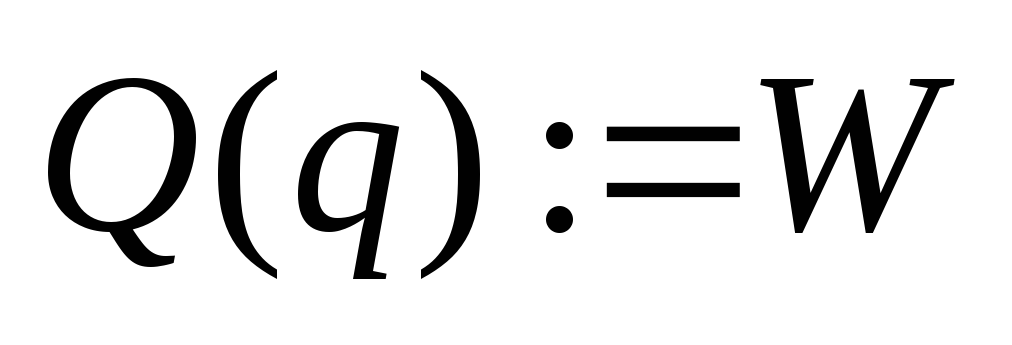 п.5.
п.5. -
Если
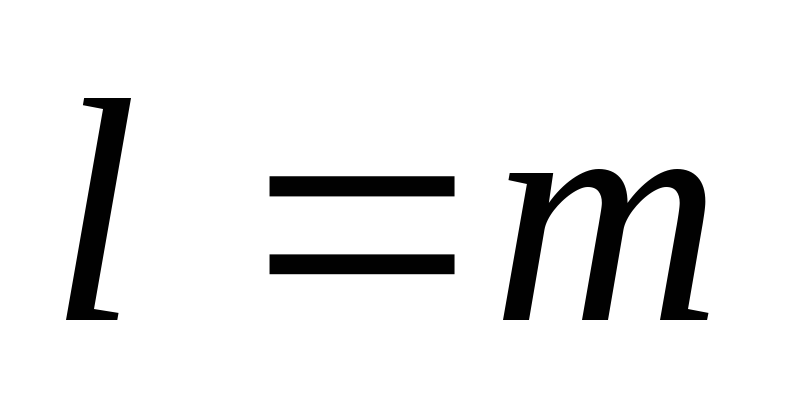 ,
то и.6, иначе
,
то и.6, иначе
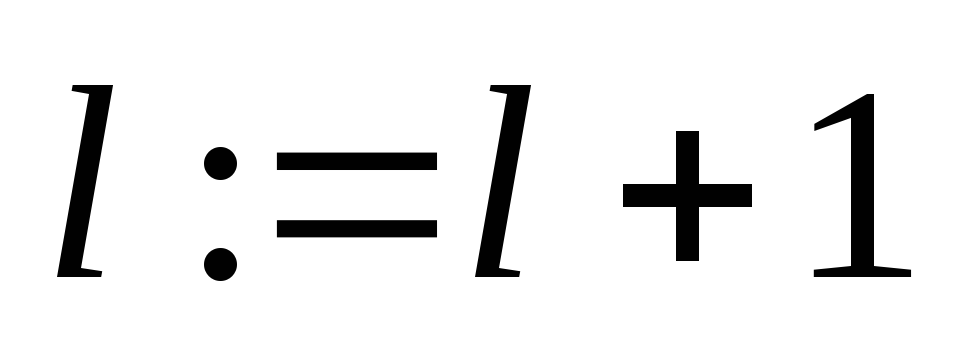 и п.4.
и п.4. -
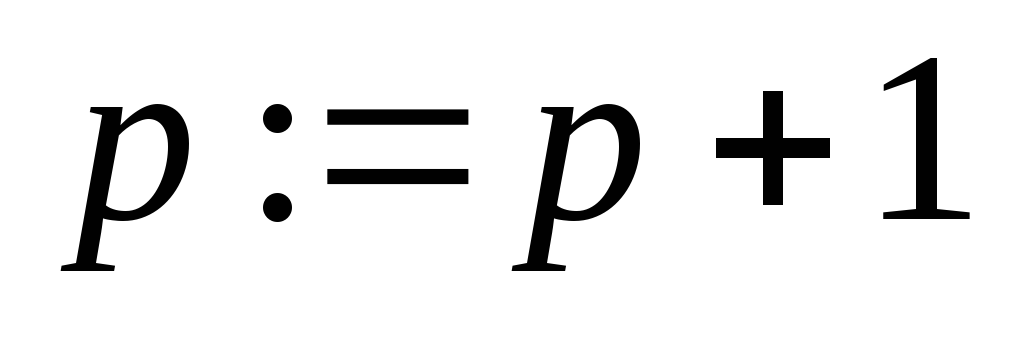 ;
; -
Если
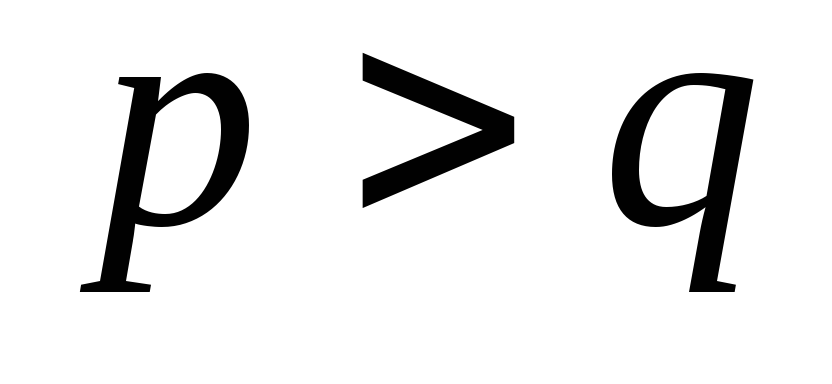 ,
то конец, иначе
п.2.
,
то конец, иначе
п.2.
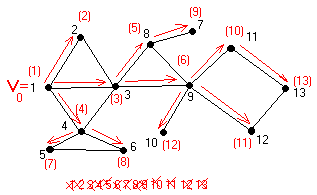
Чтобы найти остов несвязного графа, нужно для каждой компоненты связности построить дерево покрытия.
-
Остов минимального веса (кратчайший остов)
-
Граф (ориентированный или неориентированный), каждому ребру которого сопоставлено число, будем называть взвешенным. Число, сопоставленное ребру, будем называть весом или длиной ребра.
-
Остов минимального веса – остов, сумма весов рёбер которого минимальна по сравнению с другими остовами.
Замечание. Далее мы будем рассматривать взвешенные графы.
Рассмотрим следующую задачу: во взвешенном связном графе требуется найти остов минимального веса. Эта задача возникает при проектировании линий электропередачи, дорог, и т.д., когда требуется заданные центры соединить некоторой системой каналов связи так, чтобы любые два центра были связаны либо непосредственно соединяющим их каналом, либо через другие центры и каналы, и чтобы общая стоимость (или длина) каналов была минимальной.
Для решения задачи нахождения минимального остова имеются эффективные алгоритмы. Опишем некоторые из них – алгоритм Краскала и Прима, применимые к произвольно связному графу.
Задача об остове минимального веса:
В связном взвешенном графе
![]() порядка
порядка
![]() найти остов минимального веса,
найти остов минимального веса,
-
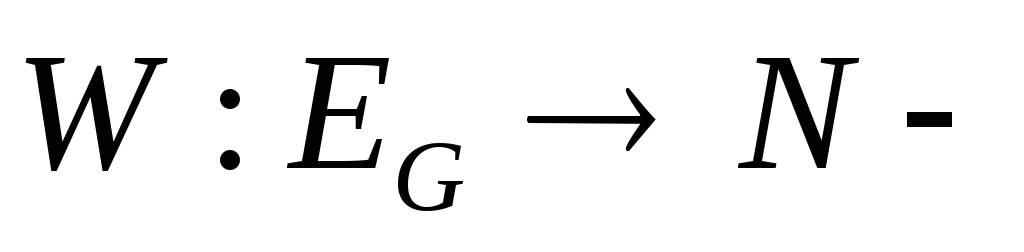 функция,
ставящая в соответствие ребру
функция,
ставящая в соответствие ребру
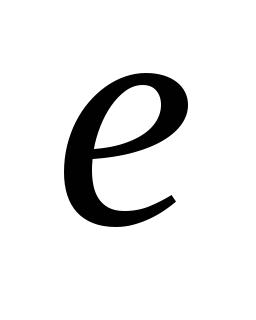 графа некоторый вес
графа некоторый вес
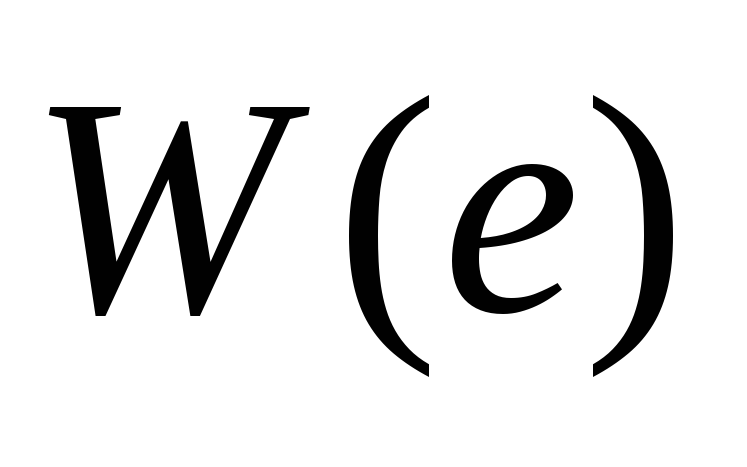 .
.
Алгоритм Краскала.
-
Строим граф
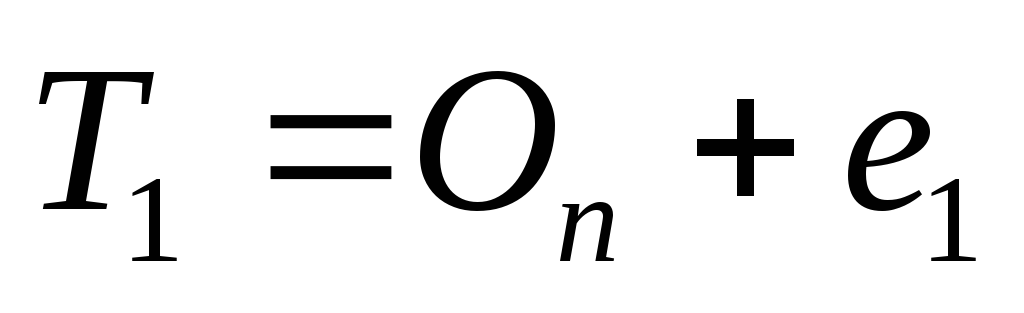 ,
присоединяя к пустому графу
,
присоединяя к пустому графу
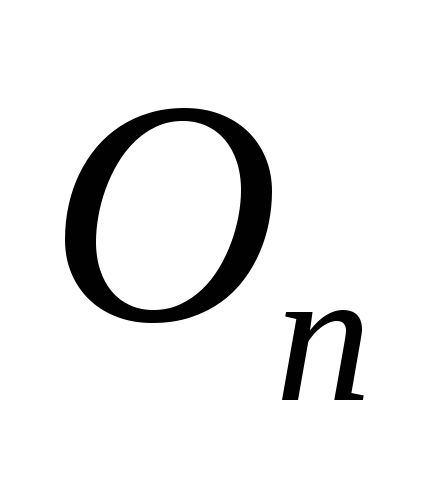 ребро
ребро
 минимального веса.
минимального веса. -
Если граф
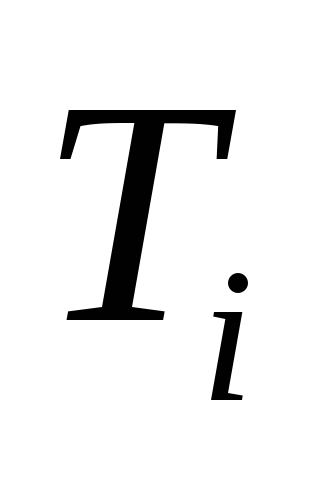 уже построен и
уже построен и
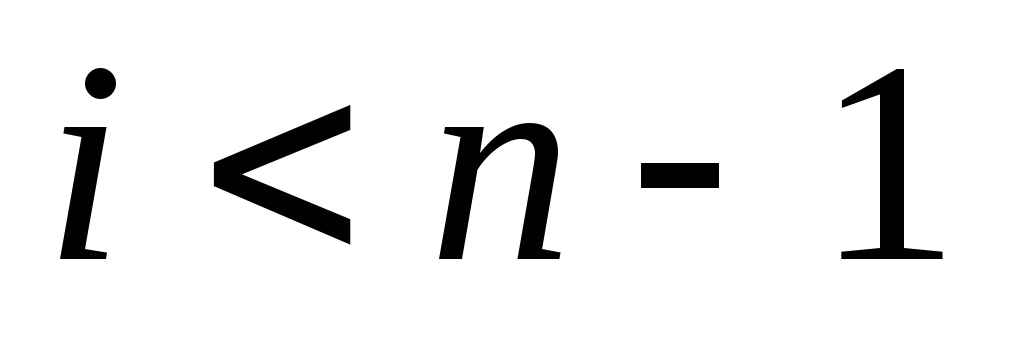 ,
то строим граф
,
то строим граф
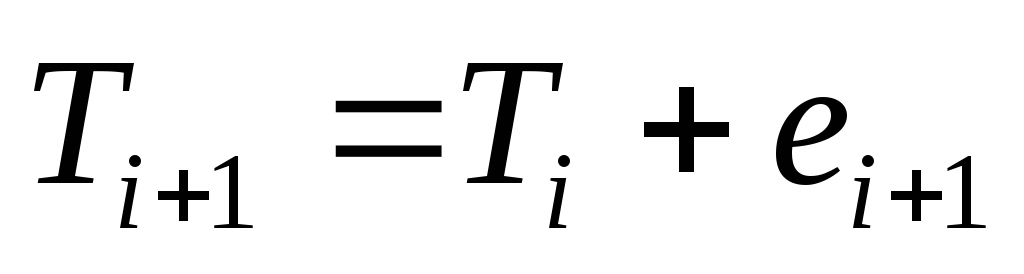 где
где
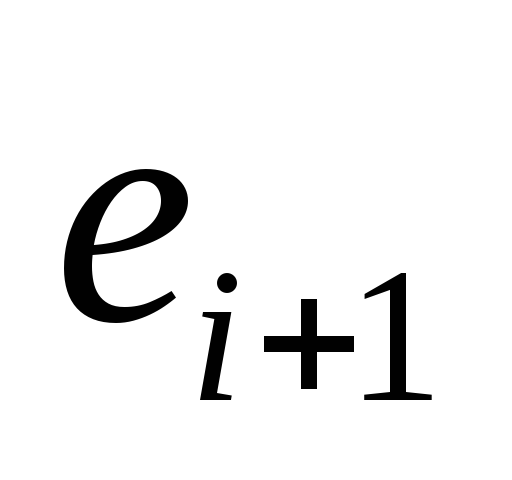 -
ребро графа
-
ребро графа
 ,
имеющее минимальный вес среди ребер,
не входящих в
,
имеющее минимальный вес среди ребер,
не входящих в
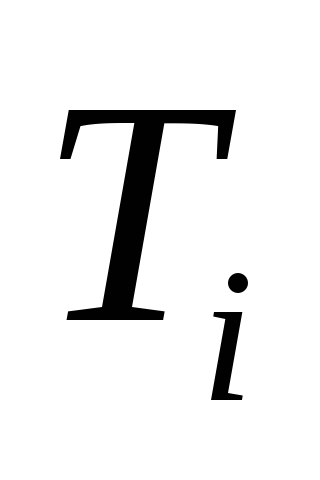 и не составляющих циклов с рёбрами из
и не составляющих циклов с рёбрами из
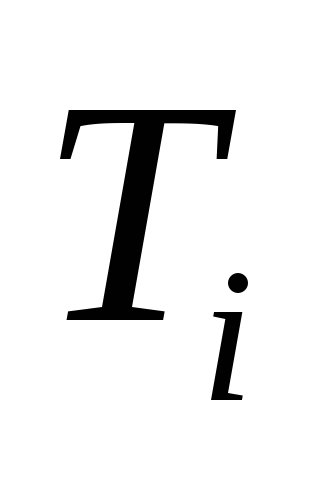 .
.
Рассмотрим граф:
Алгоритм Прима.
-
Выбираем ребро
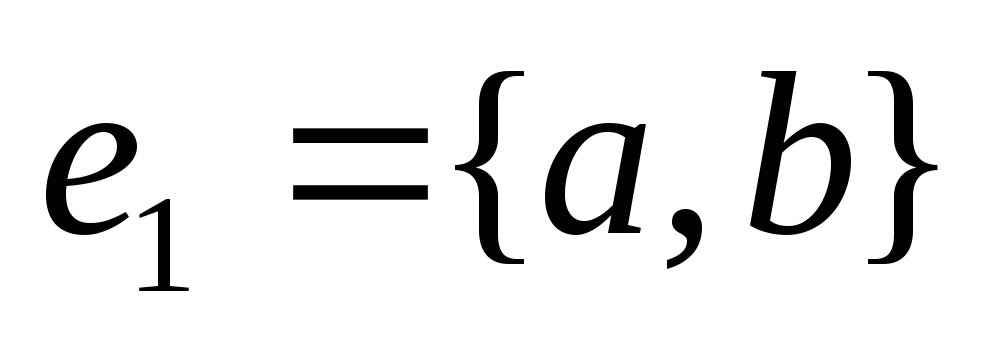 минимального веса и строим дерево
минимального веса и строим дерево
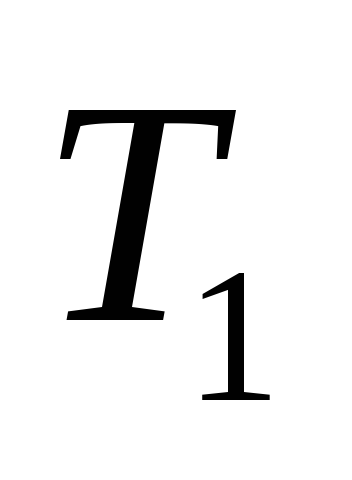 ,
пологая
,
пологая
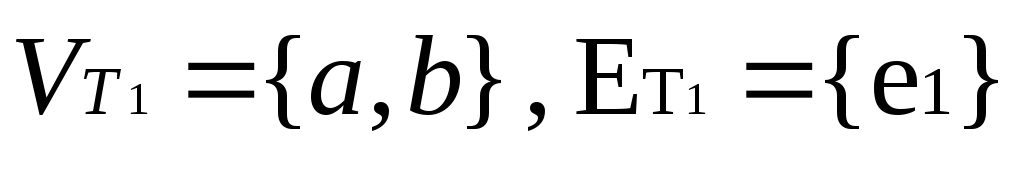 .
. -
Если дерево
 порядка
порядка
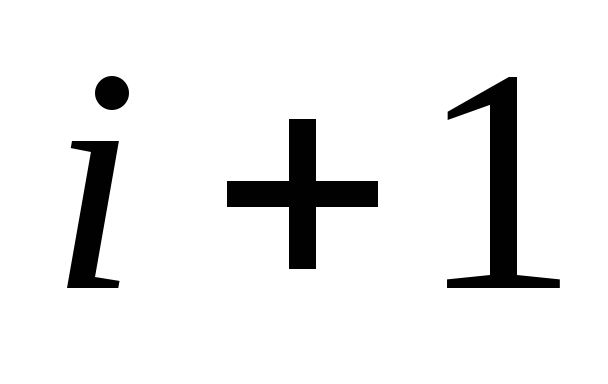 - уже построена и
- уже построена и
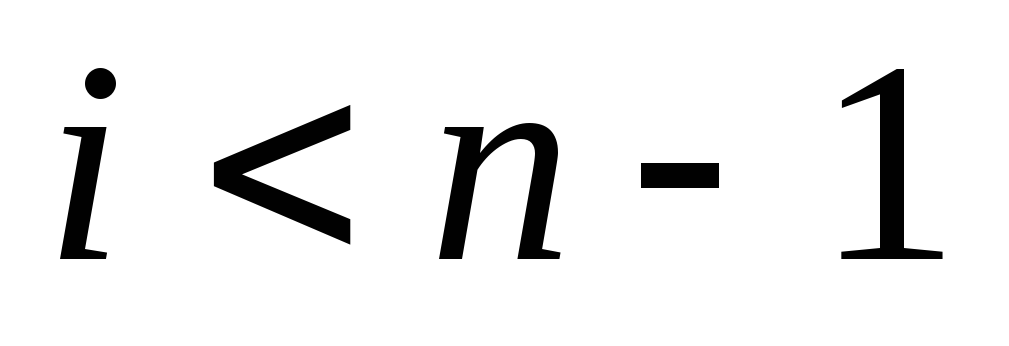 ,
то среди рёбер, вершины этого дерева с
вершинами графа
,
то среди рёбер, вершины этого дерева с
вершинами графа
 ,
не входящими в
,
не входящими в
 ,
выбираем ребро
,
выбираем ребро
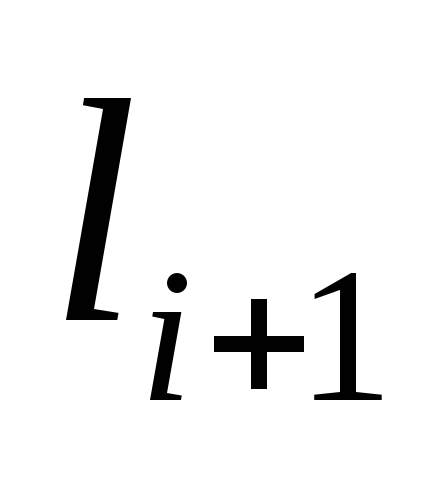 минимального веса. Строим дерево
минимального веса. Строим дерево
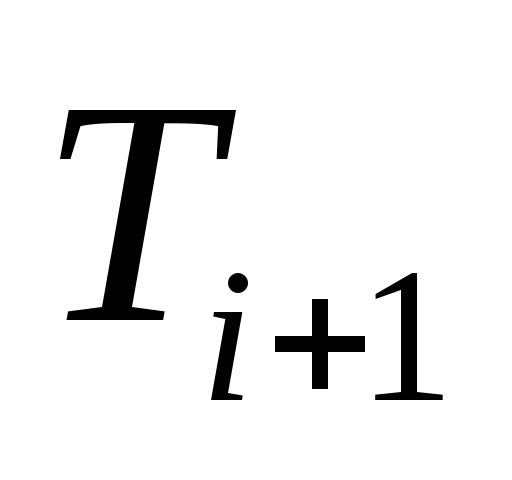 ,
присоединяя к
,
присоединяя к
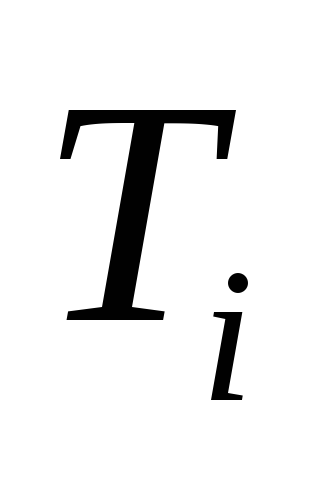 ребро
ребро
 вместе с его не входящими в
вместе с его не входящими в
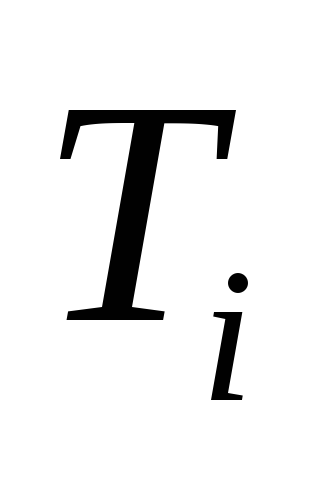 концами.
концами.
В некоторых ситуациях требуется построить остов не минимального а, максимального веса. К этой задаче также применимы оба алгоритма. Следует только всюду минимальный вес заменять на максимальный.
-
Кратчайшие пути
Пусть
![]() -
ориентированный взвешенный граф.
-
ориентированный взвешенный граф.
Задача о кратчайшем пути состоит в
отыскании пути минимального веса,
соединяющего задание начальную и
конечную вершину графа
![]() при условии, что хотя бы 1 такой путь
при условии, что хотя бы 1 такой путь
![]() ет.
Начальную и конечную вершины обозначим
соответственно через
ет.
Начальную и конечную вершины обозначим
соответственно через
![]() и
и
![]() .
.
![]() -
путь минимального веса будем называть
кратчайшим
-
путь минимального веса будем называть
кратчайшим
![]() путём.
путём.
-
Алгоритм Дейкстра
Вначале рассмотрим случай, когда веса
всех дуг неотрицательны, т.е.
![]() для каждой дуги
для каждой дуги
![]() .
В этом случае решение задачи о кратчайшем
пути является мене трудоёмким, чем в
общем случае.
.
В этом случае решение задачи о кратчайшем
пути является мене трудоёмким, чем в
общем случае.
Первый эффективный алгоритм построения кратчайшего пути в графе с неотрицательными весами дуг предложил Дейкстра в 1959.
На каждой итерации этого алгоритма
всякая вершина
![]() графа
графа![]() имеет метку
имеет метку
![]() ,
которая может быть постоянной или
временной. В первом случае
,
которая может быть постоянной или
временной. В первом случае
![]() -вес
кратчайшего
-вес
кратчайшего
![]() -
пути. Если же метка
-
пути. Если же метка
![]() временная, то
временная, то
![]() -
вес кратчайшего пути,
-
вес кратчайшего пути,
![]() -пути,
проходящего только через вершины с
постоянными метками. Т.о., временная
метка
-пути,
проходящего только через вершины с
постоянными метками. Т.о., временная
метка
![]() является оценкой сверху для веса
кратчайшего
является оценкой сверху для веса
кратчайшего
![]() -
пути, и став на некоторой итерации
постоянной, она остается такой до конца
работы алгоритма.
-
пути, и став на некоторой итерации
постоянной, она остается такой до конца
работы алгоритма.
Кроме
![]() ,
с каждой вершиной
,
с каждой вершиной
![]() графа
графа
![]() ,
за исключением
,
за исключением
![]() ,
связывается ещё одна метка
,
связывается ещё одна метка
![]() .
На каждой итерации
.
На каждой итерации
![]() является номером вершины, предшествующей
является номером вершины, предшествующей
![]() в
в
![]() - пути имеющем минимальный вес среди
всех
- пути имеющем минимальный вес среди
всех
![]() -
путей, проходящих через вершины,
получившие к этому моменту постоянные
метки. После того, как вершина
-
путей, проходящих через вершины,
получившие к этому моменту постоянные
метки. После того, как вершина
![]() получила постоянную метку. С помощью
меток
получила постоянную метку. С помощью
меток
![]() легко указать последовательность
вершин, составляющий кратчайший
легко указать последовательность
вершин, составляющий кратчайший
![]() -
путь.
-
путь.
Перед началом первой итерации алгоритма
вершина
![]() имеет постоянную метку
имеет постоянную метку
![]() ,
а метки всех остальных вершин
,
а метки всех остальных вершин
![]() и эти метки временные.
и эти метки временные.
Будем считать, что граф
![]() задан матрицей весов либо списками
смежности.
задан матрицей весов либо списками
смежности.
