
- •Алгоритмы на графах
- •Обходы графов
- •Поиск в глубину (пг)
- •Алгоритм поиска в глубину в неориентированном связном графе
- •Поиск в ширину (пш)
- •Алгоритм поиска в ширину в неориентированном связном графе
- •Нахождение деревьев и остовов с помощью пг и пш
- •Нахождение дерева покрытия с помощью .
- •Нахождение дерева покрытия с помощью
- •Остов минимального веса (кратчайший остов)
- •Задача об остове минимального веса:
- •Алгоритм Краскала.
- •Алгоритм Прима.
- •Кратчайшие пути
- •Алгоритм Дейкстра
- •Алгоритм Дейкстра поиска кратчайшего пути.
- •Алгоритм Флойда
- •Алгоритм Флойда
-
Алгоритмы на графах
-
Обходы графов
-
Обход графа – это некоторое перечисление его вершин (и/или ребер). Среди всех обходов наиболее известны поиск в глубину и в ширину. Алгоритмы поиска в глубину и в ширину лежат в основе многих алгоритмов на графах.
-
Поиск в глубину (пг)
Пусть граф
![]() задан списками смежности, т.е.
задан списками смежности, т.е.
![]() задан
задан
![]() -
список вершин, инцидентных вершине
-
список вершин, инцидентных вершине
![]() ,
и пусть задана исходная вершина
,
и пусть задана исходная вершина
![]() ,
с какой начинается поиск.
,
с какой начинается поиск.
Результат работы алгоритма – 2 списка:
![]() ,
,
![]() ,
,
-

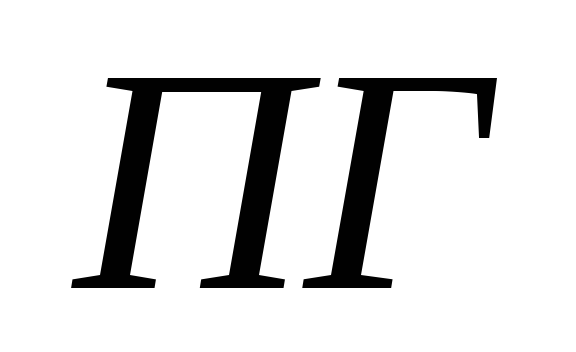 -номер
вершины
-номер
вершины
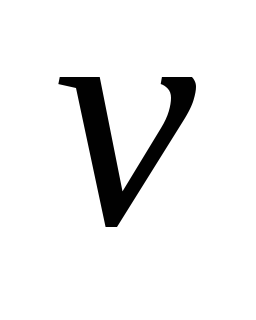 ,
,
![]() имя
вершины, из которой вершина
имя
вершины, из которой вершина
![]() получила свой номер.
получила свой номер.
В процессе работы алгоритма используется
стек
![]() .
.
Алгоритм поиска в глубину в неориентированном связном графе
-
 ;
;
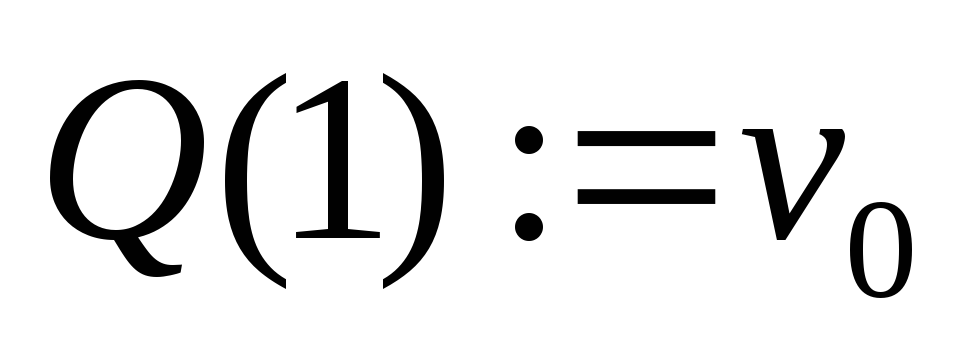 ;
;
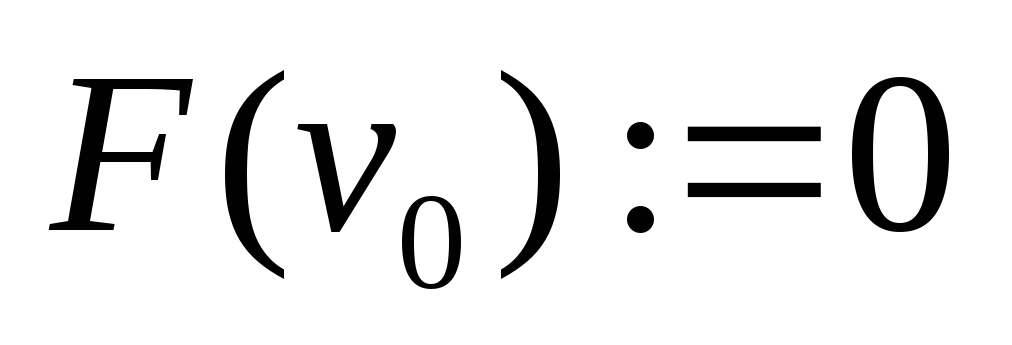 ;
;
![]() ;
//
;
//
![]() -
последний присваиваемый
-
последний присваиваемый
![]() номер
номер
![]() ;
//
;
//
![]() -
указатель конца стека
-
указатель конца стека
![]() ,
т.е.
,
т.е.
![]() имя
последней вершины стека
имя
последней вершины стека
![]() .
.
-
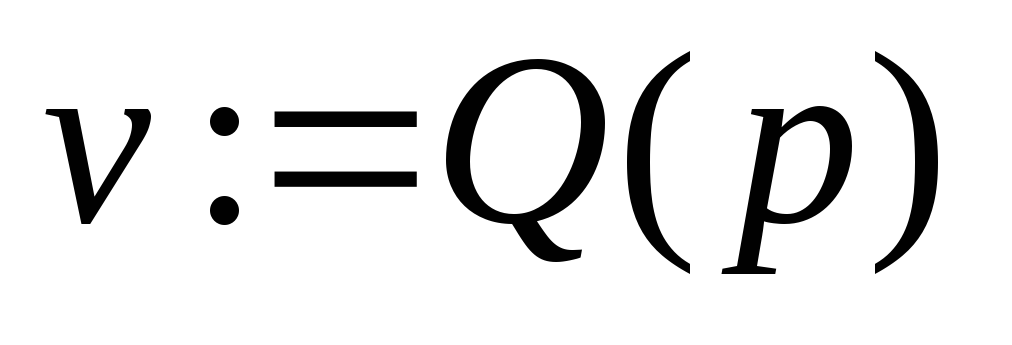 ;
//
;
//
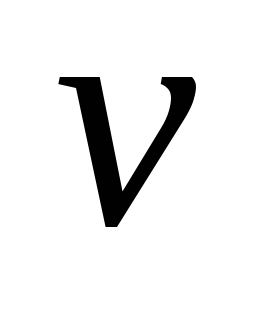 -
исследуемая вершина
-
исследуемая вершина -
Просматривая список
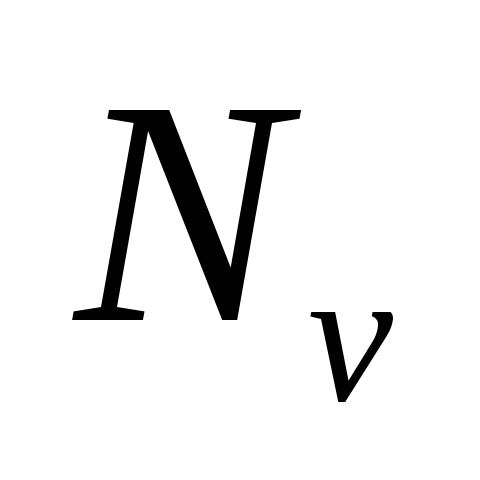 ,
найти новую ещё не просмотренную вершину
,
найти новую ещё не просмотренную вершину
 ,
и перейти к п.4. Если все вершины в списке
,
и перейти к п.4. Если все вершины в списке
 уже просмотрены, то перейти к п.5
уже просмотрены, то перейти к п.5 -
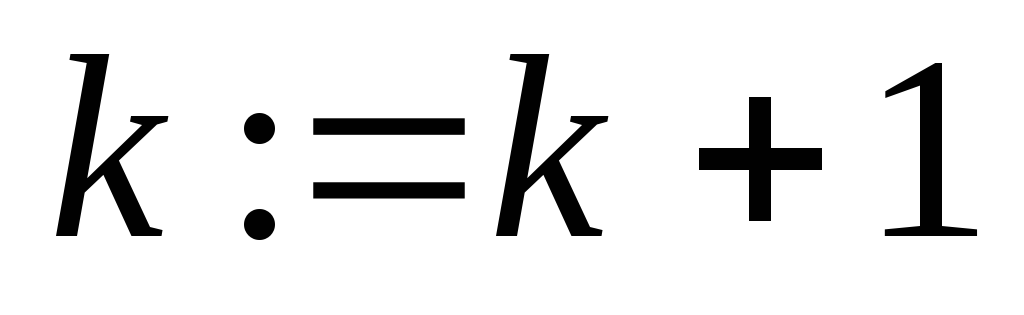 ;
;
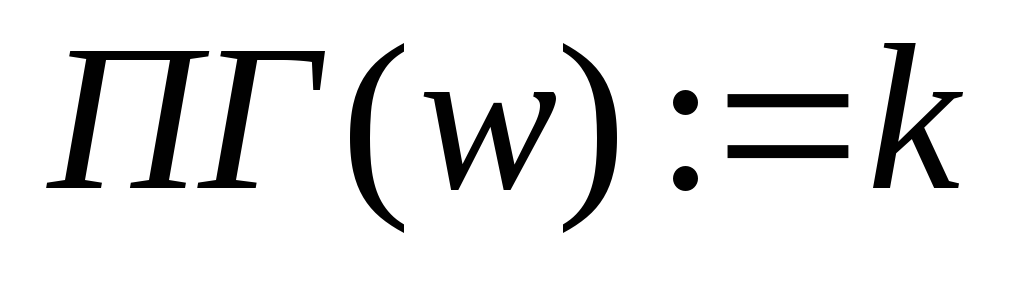 ;
;
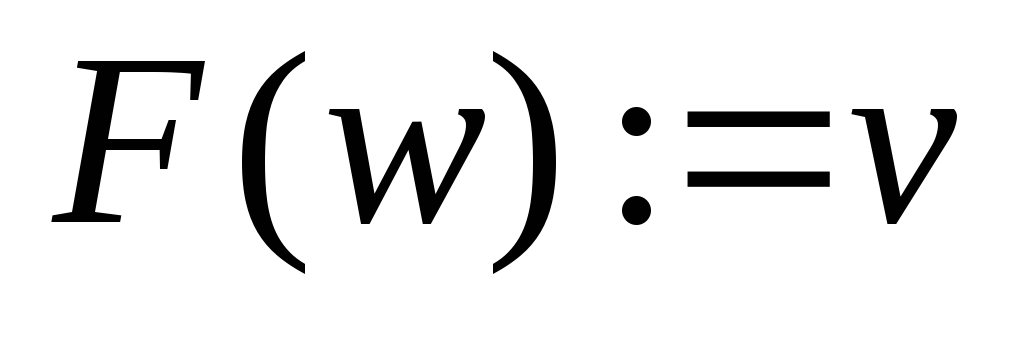 ;
;
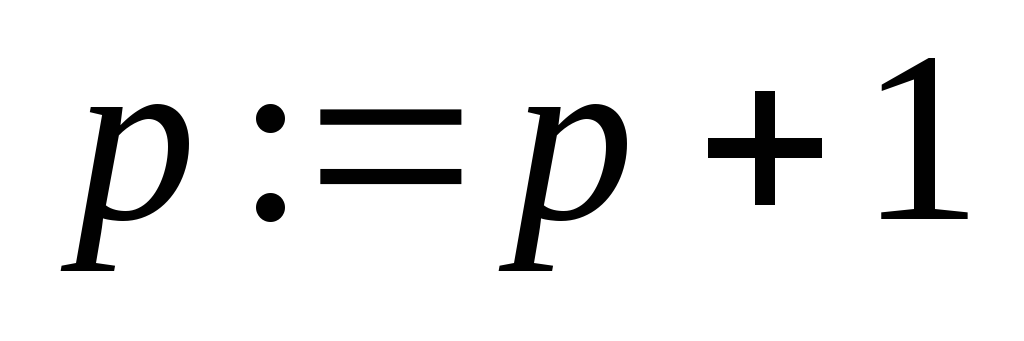 ;
;
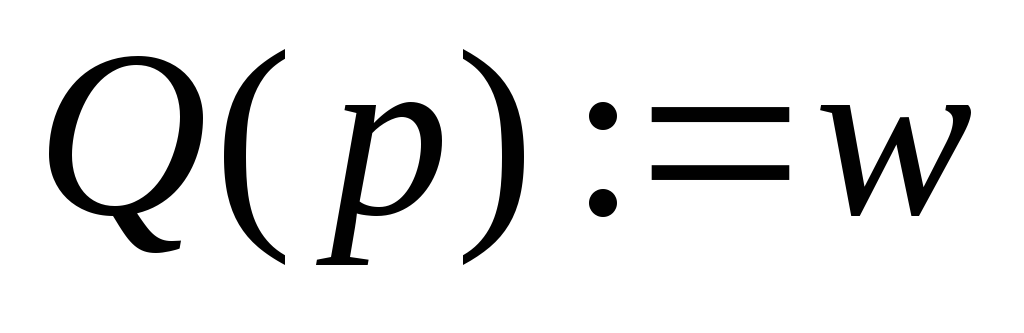 ;
вершина
;
вершина
 получила
получила
 - номер и занесена в стек
- номер и занесена в стек
 .
. -
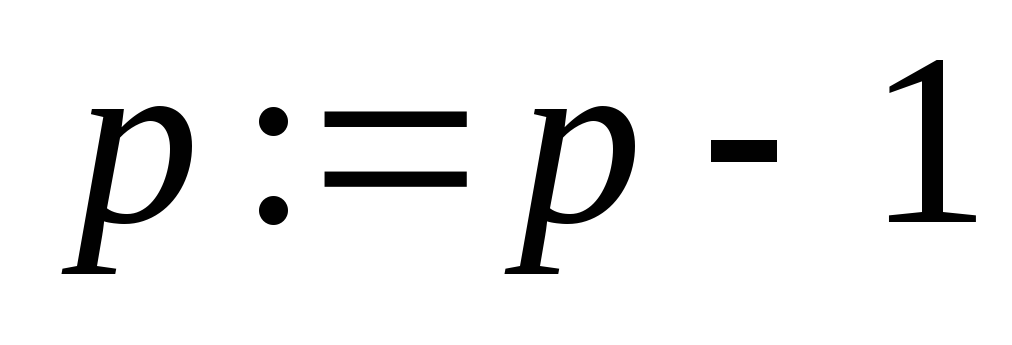 ;
// вершина
;
// вершина
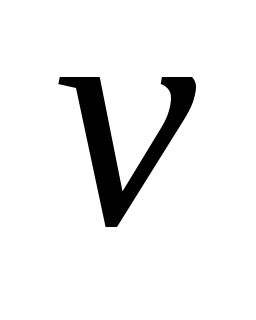 вычеркнута из
вычеркнута из
 .
Если
.
Если
 ,
то конец. Иначе перейти к п.2.
,
то конец. Иначе перейти к п.2.
-
Поиск в ширину (пш)
Заметим, что при поиске в глубину, чем
позднее была посещена, тем раньше она
будет использована (стек). При
![]() чем раньше посещается вершина, тем
раньше оно используется (очередь).
чем раньше посещается вершина, тем
раньше оно используется (очередь).
Пусть
![]() задан списками смежности и пусть задана
исходная вершина
задан списками смежности и пусть задана
исходная вершина
![]() ,
с какой начинается поиск. В процессе
работы алгоритма используется очередь
,
с какой начинается поиск. В процессе
работы алгоритма используется очередь
![]() .
Вначале в
.
Вначале в
![]() имеется единственная вершина
имеется единственная вершина
![]() .
.
Алгоритм поиска в ширину в неориентированном связном графе
1. ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
// адрес первой занятой ячейки списка
;
// адрес первой занятой ячейки списка
![]()
![]() ;
// адрес последней занятой ячейки списка
;
// адрес последней занятой ячейки списка
![]()
![]() ;
// последний
;
// последний
![]() ый
ый
![]() номер
номер
-
 ;
// выбрана первая вершина очереди
;
// выбрана первая вершина очереди

![]() ;
// количество вершин, смежных с
;
// количество вершин, смежных с
![]()
-
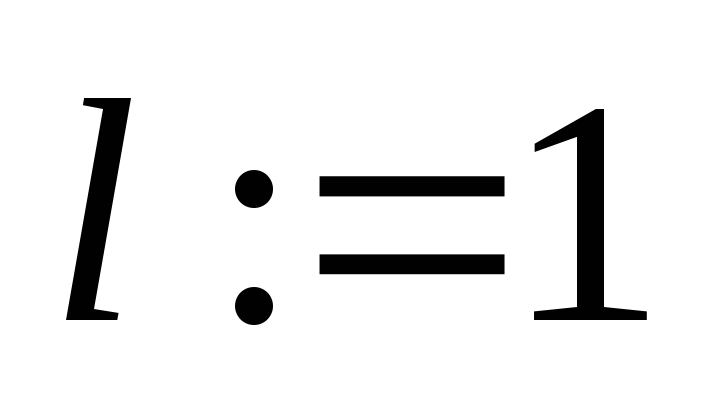 ;
; -
Если вершина
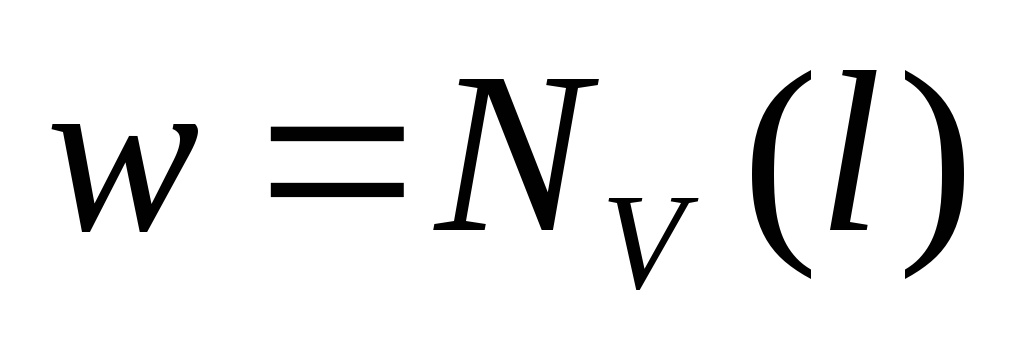 уже просмотрена, то перейти к п.5.
уже просмотрена, то перейти к п.5.
Иначе
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
// вершина
;
// вершина
![]() помечена и включена в
помечена и включена в
![]() и перейти к п.5.
и перейти к п.5.
-
Если
 ,
то перейти к п.6, иначе
,
то перейти к п.6, иначе
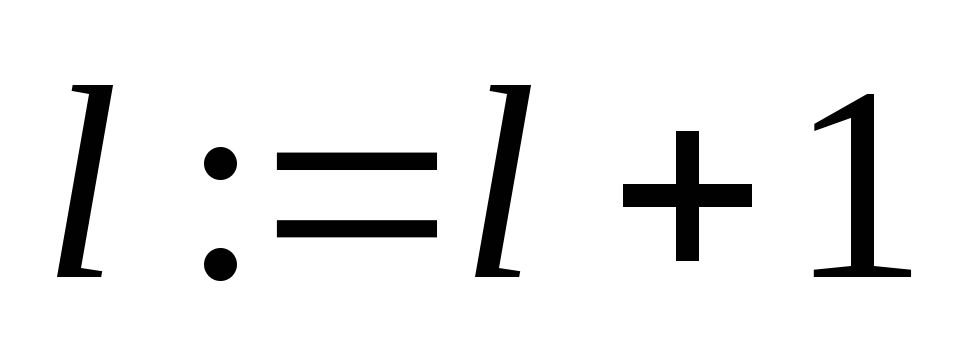 и следовать к п.4
и следовать к п.4 -
 ;
// вершина
;
// вершина
 исключена из
исключена из
 .
. -
Если
 ,
то конец //
,
то конец //
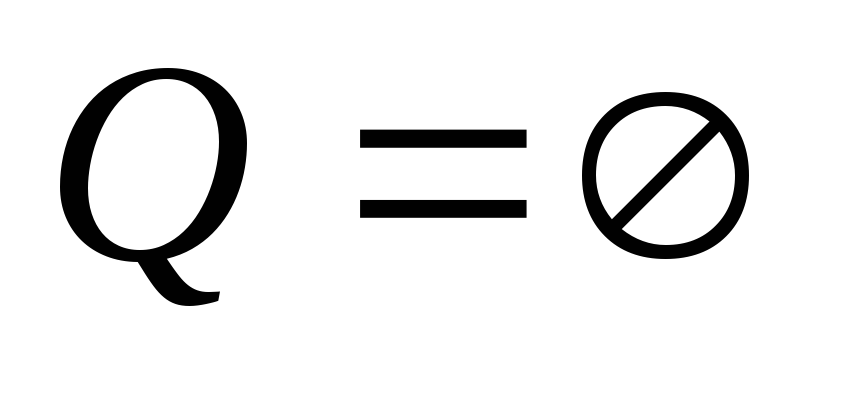 ,
т.е. все вершины помечены. Иначе следовать
к п.2.
,
т.е. все вершины помечены. Иначе следовать
к п.2.
-
Нахождение деревьев и остовов с помощью пг и пш
Пусть
![]() -
связный граф (неориентированный). Пусть
-
связный граф (неориентированный). Пусть
![]() его дерево покрытия. Рёбра этого дерева
будим называть ветвями, а все
остальные рёбра графа – хордами.
его дерево покрытия. Рёбра этого дерева
будим называть ветвями, а все
остальные рёбра графа – хордами.
Процедуры
![]() и
и
![]() можно простым способом использовать
для нахождения деревьев покрытия. В
обоих случаях достижение вершины
можно простым способом использовать
для нахождения деревьев покрытия. В
обоих случаях достижение вершины
![]() из вершины
из вершины
![]() вызывает включение в дерево дуги
вызывает включение в дерево дуги
![]() .
.
Нахождение дерева покрытия с помощью .
Результат работы алгоритма – дерево
покрытия (ориентированное). Пусть
![]() - вершина, с которой начинается поиск.
- вершина, с которой начинается поиск.
1.![]() ;
;
![]() ;
// множество найденных ветвей
;
// множество найденных ветвей
![]() ;
// указатель конца стека
;
// указатель конца стека
-
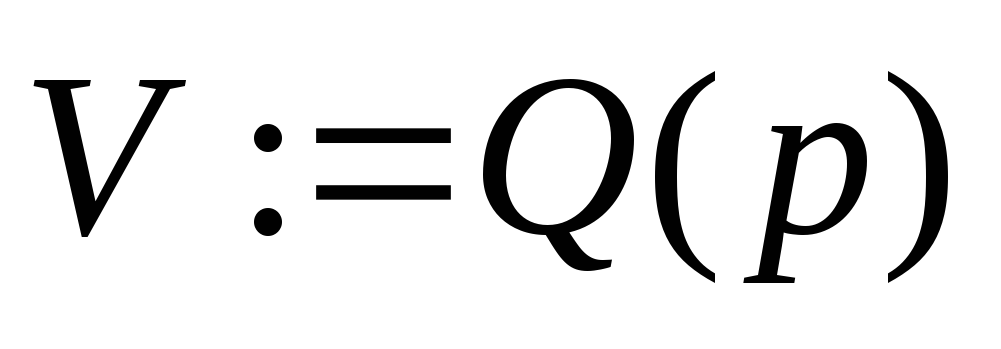 ;
; -
Просматривая список
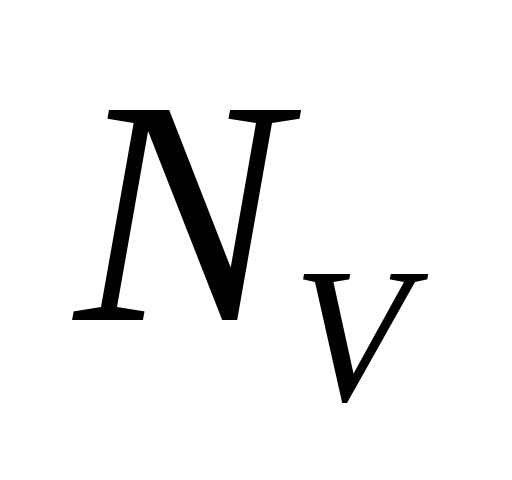 ,
найти новую, ещё не просмотренную
вершину
,
найти новую, ещё не просмотренную
вершину
 ,
и перейти к п.4. Если таких вершин нет,
то следовать к п.5.
,
и перейти к п.4. Если таких вершин нет,
то следовать к п.5. -

 ;
;
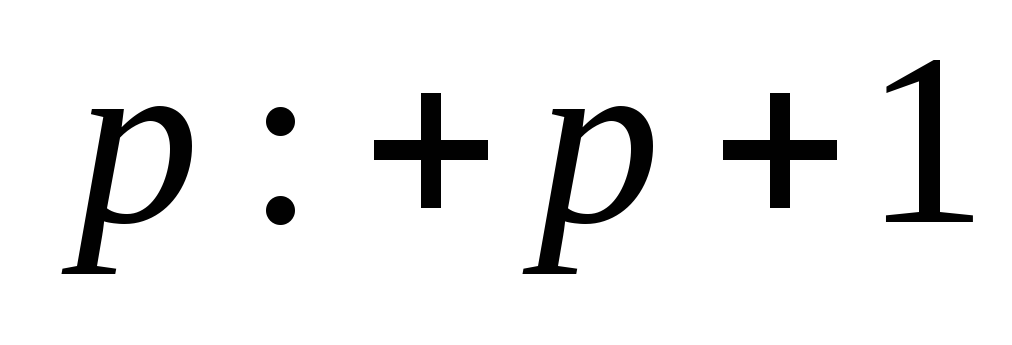 ;
;
 ;
Перейти к п.2.
;
Перейти к п.2. -
 .
Если
.
Если
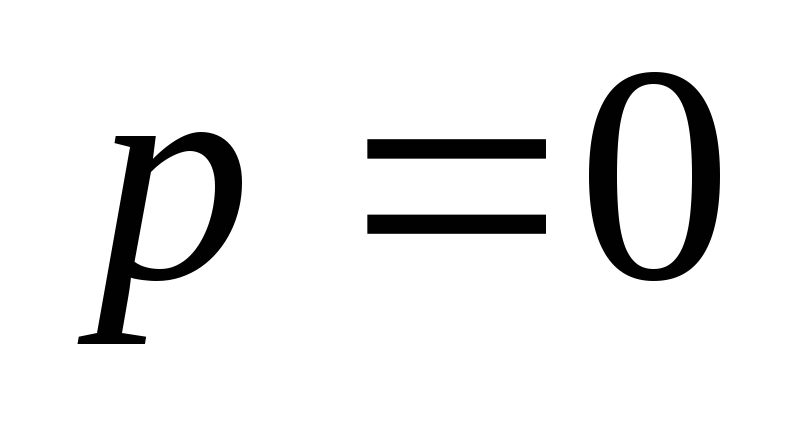 ,
то конец. Иначе следовать к п.2.
,
то конец. Иначе следовать к п.2.

Вершину
![]() ,
с которой мы начинали поиск в графе,
назовём корнем дерева покрытия
,
с которой мы начинали поиск в графе,
назовём корнем дерева покрытия
![]() .
.
