1.3.2. Операции над нечеткими множествами

Операции над нечеткими множествами определим как операции над функциями принадлежности. Здесь .

1. Объединение нечетких множеств и

.

2. Пересечение нечетких множеств и

.

3. Абсолютное дополнение(или просто дополнение) комплекта

.

4. Относительное дополнениенечёткого множества до нечеткого множества(разность)

.

5. Симметрическая разность(дизъюнктивная сумма)

.

Пример.Даны нечеткие множества:,,. Составить функции принадлежности и выполнить операции:,,.

Решение.

Универсальное множество

.

Функции принадлежности

,

.

1. Объединение

.

2. Пересечение

.

3. Абсолютное дополнение (дополнение)

.

4. Относительное дополнение (разность)

5. Симметрическая разность (дизъюнктивная сумма)

Задание 1. Формирование множеств, комплектов, нечетких множеств. Проверка законов теории множеств Условие

1.1. Сформировать множества A,B,Cиз букв, входящих соответственно в фамилию, имя, отчество студента. В качестве универсального принять множествоU=ABC. Указать мощности множеств:.

1.2. Проверить наличие отношений включения, равенства, эквивалентности.

1.3. Составить характеристические функции .

1.4. Проверить все законы теории множеств на множествах и характеристических функциях.

2.1. Сформировать комплекты .

2.2. Составить функции экземплярности .

2.3. Проверить на функциях экземплярности следующие законы теории множеств:

• один из законов дистрибутивности;

• один из законов де Моргана;

• один из законов поглощения;

• законы дополнения ;

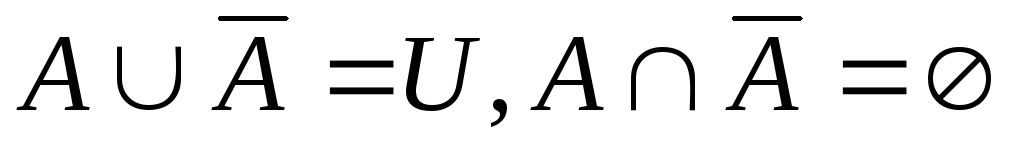• закон инволюции .

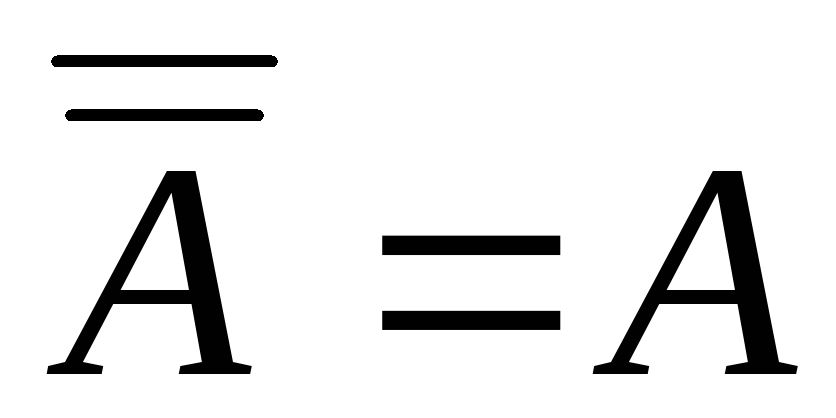3.1. На основе комплектов составить функции принадлежности .

3.2. Проверить на функциях принадлежности законы теории множеств, указанные в п. 2.3.

Решение

Иванов Кирилл Алексеевич

1.1. Формирование множеств

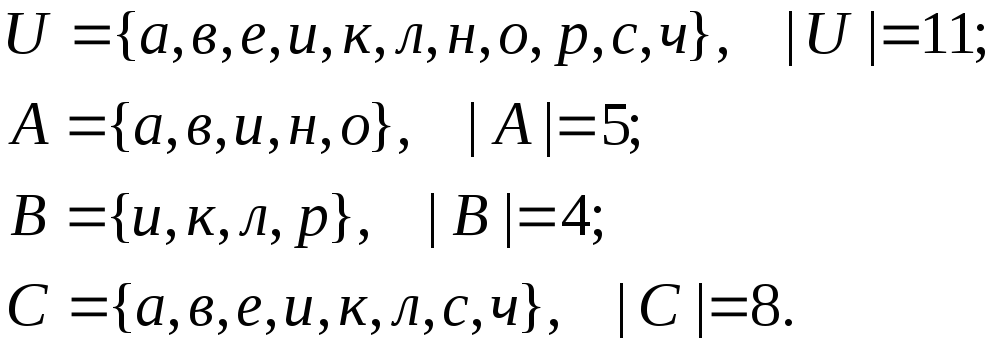
1.2. Отношение включения. Рассмотрим отношение включения множествА,В,СиUмежду собой.

– по условию задачи. Кроме того, так как, ,, то множестваА,В,Сявляются строгими подмножествами универсального множестваU, т.е..

, так как существует элемент множестваА, который не принадлежит множествуВ, например, но.

, так как существует элемент множестваВ, который не принадлежит множествуА, например, но.

, так как существует элемент множестваА, который не принадлежит множествуС, например, но.

, так как существует элемент множестваС, который не принадлежит множествуА, например, но.

, так как существует элемент множестваВ, который не принадлежит множествуС, например, но.

, так как существует элемент множестваС, который не принадлежит множествуВ, например, но.

Отношение равенства

Так как , но, то.

Так как , но, то.

Так как , но, то.

Так как и, то.

Так как и, то.

Так как и, то.

Отношение эквивалентности

Множества являются эквивалентными, если их мощности равны.

Так как , то(,,).

Так как , то.

Так как , то.

Так как , то.

1.3. Характеристические функции

1.4. Проверка законов теории множеств

Законы коммутативности

а) .

.

б) .

.

Законы ассоциативности

а)

б)

Законы дистрибутивности

а)

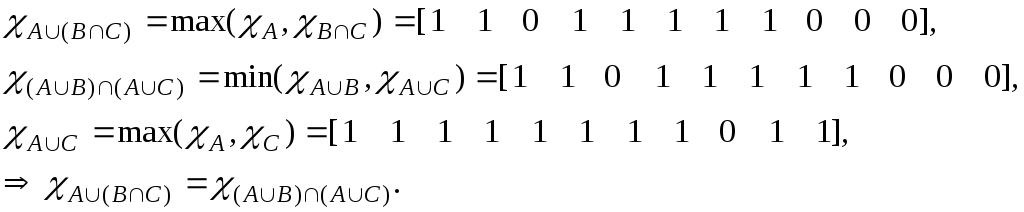
б)

Законы де Моргана

а)

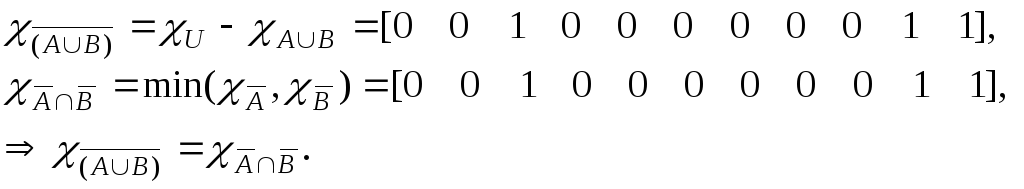
б)

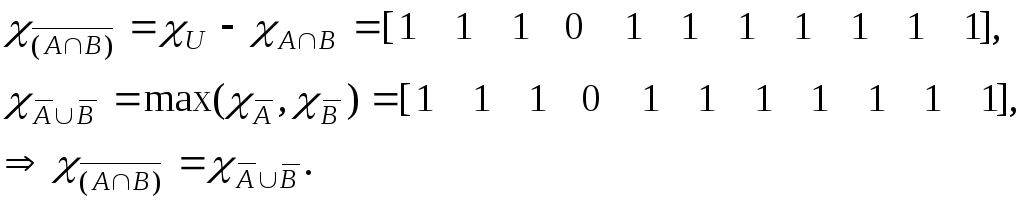
Законы идемпотентности

а)

б)

Законы поглощения

а)

б)

Законы тождества

а) 

б)

Законы констант

а)

б) 

Законы дополнения

а)

б)

в) ;.

г) ;

Закон инволюции

2.1. Формирование комплектов

2.2. Функции экземплярности

2.3. Проверка законов теории множеств

Закон дистрибутивности

Закон де Моргана

Закон поглощения

Законы дополнения

а)

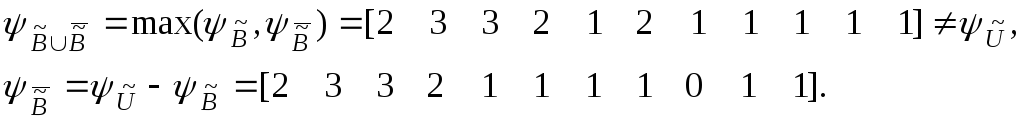
б)

Закон инволюции

3.1. Формирование функций принадлежности нечетких множеств

3.2. Проверка законов теории множеств

Закон дистрибутивности

Закон де Моргана

Закон поглощения

Законы дополнения

а)

б)

Закон инволюции