
Ответы на вопросы к экзамену 2011
.pdf
Вопрос №13. Равносильности формул. |
|
|
|
Для любых формул А, В, С справедливы следующие равносильности: |
|
||
1) |
А В В А (коммутативность ); |
|
|
2) |
А В В А (коммутативность ); |
|
|
3) |
А (В С) (А В) С (ассоциативность ); |
|
|
4) |
А (В С) (А В) С (ассоциативность ); |
|
|
5) |
А (В С) (А В) ( А С) |
(дистрибутивность |
|
относительно ); |
|
|
|
6) |
А (В С) (А В) (А С) |
(дистрибутивность |
|
относительно ); |
|
|
|
7)( А В) А В (первый закон де Моргана);
8)( А В) А В (второй закон де Моргана);
9)А А А (идемпотентность );
10)А А А (идемпотентность );
11)А (А В) А (первая формула поглощения);
12)А (А В) А (вторая формула поглощения);
13)А И А (первый закон тождества);
14)А Л А (второй закон тождества);
15)А И И (первый закон констант);
16)А Л Л (второй закон констант);
17)А А И (первая формула дополнения);
18)А А Л (вторая формула дополнения);
19)А (А В) (А В) (первая формула расщепления);
20)А (А В) (А В) (вторая формула расщепления);
21)А А (снятие двойного отрицания).
22)А ~ В (А В) (В А) (А В) (А В);
23)А В А В ( А В ) ;
24)А В А В ( А В ) ;
25)А В ( А В ) ( А В ) ;
26)А В (А В) (А В);
27)A | B ( A B) ;
28)A B ( A B) .
10

Вопрос №14. Закон двойственности.
Определение двойственности. Пусть X1,..., Xn – все входящие в формулу
|
|
|
|
|
|
|
|
А элементарные высказывание. Формула А* ( X1 ,..., X n ) |
A |
(X1 ,..., X n ) |
называется |
||||
двойственной к формуле A . Очевидно, что A** совпадает с А. |
|
||||||
Теорема (закон двойственности). Если формулы А и В равносильны друг |
|||||||
другу, то и двойственными к ним также равносильны, т.е. если |
А В , то и |
||||||
А* В* . |
|
||||||
Доказательство. Пусть А( X1 ,..., X n ) B(X1 ,..., X n ), где X1 ,..., X n – входящие в |
|||||||
них элементарные высказывания. Тогда |
|
||||||
A* ( X1 ,..., X n ) A(X1 ,..., X n ) и B* ( X1 ,..., X n ) B (X1 ,..., X n ) .
Формулы А( X1,..., Xn ) и B( X1,..., Xn ) принимают одинаковые значения при любых значениях переменных X1 ,..., X n . Следовательно, А и В будут равносильны и при переменных X 1,..., X n , т.е. A( X 1 ,..., X n ) B( X 1 ,..., X n ) . Применим операцию отрицание к формуле. Значение формул Л поменяется на значение И, а И – на Л. Но формулы при этом останутся равносильными, т.е.
|
|
|
|
|
|
|
|
|
n ) |
|
|
|
|
|
|
n ) . |
Таким |
образом, |
так |
как |
|||||||
А( |
X |
1 ,..., |
X |
B |
( |
X |
1 ,..., |
X |
|||||||||||||||||||
|
|
|
|
|
|
|
B* |
|
( |
|
1 ,..., |
|
n ) , получаем А* В* . |
|
|
||||||||||||
A* |
А |
(X1 ,..., X n ), |
B |
X |
X |
|
|
||||||||||||||||||||
|
|
|
|
|
Доказательство завершено. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
Вопрос №15. Тождественно истинные и ложные формулы. |
|
|||||||||||||||||||||
|
|
|
|
|
Пусть формула А зависит от списка переменных X1,..., Xn . |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формула |
А |
называется |
тавтологией |
(или |
||||||||
|
|
|
|
|
|
|
|
|
|
|
тождественно-истинной формулой), если на любых оценках |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
списка переменных X1,..., Xn |
она принимает значение И. |
|
||||||||||||||
Пример. X X .
Формула А называется выполнимой, если на некоторой оценке списка переменных X1,..., Xn она принимает значение И.
Пример. X Y .
Формула А называется тождественно-ложной, если на любых оценках списка переменных она принимает значение Л.
X X .
Формула А называется опровержимой, если на некоторой оценке списка переменных X1,..., Xn она принимает значение Л.
Пример. X Y . Утверждение.
11

1)А – тавтология А не является опровержимой.
2)А – тождественно-ложна А не является выполнимой.
3)А – тавтология А – тождественно-ложна.
4)А – тождественно-ложна А – тавтология.
5)А~В– тавтология А≡В.
Ниже указаны наиболее важные тавтологии (А, В, С – произвольные формулы).
|
|
|
|
|
|
|
|
|
|
1) |
А А (закон исключающего третьего); |
||||||||
2) |
А А; |
|
|||||||
3) |
А (В А) ; |
|
|||||||
4) |
(А В) ((В С) (А С)) (цепное рассуждение); |
||||||||
5) |
(А (В С)) ((А В) (А С)) ; |
||||||||
6) |
(А В) А, |
( А В) В ; |
|||||||
7) |
А (В (А В)) ; |
||||||||
8) |
А (А В), В (А В) ; |
||||||||
|
|
|
|
|
|
|
|
||
9) |
( |
В |
А) (( |
В |
А) В) ; |
||||
10) |
((А В) А) А (закон Пирса). |
||||||||
Каждую из этих тавтологий можно обосновать, например, составив таблицу истинности при произвольных значениях А, В, С.
Вопрос №16. Нормальные формы.
Формула находится в дизъюнктивной нормальной форме (ДНФ), если она является дизъюнкцией элементарных (возможно, одночленной)
конъюнкций. |
Например, |
формулы |
, |
̅̅̅, |
, |
||
( |
̅̅̅) ( |
̅̅̅ |
). |
|
|
|
|
|
Говорят, что формула |
находится в конъюнктивной нормальной форме |
|||||
(КНФ), если формула |
определена (то есть в |
нет символов |
и ) и |
||||
находится в ДНФ. |
|
|
|
|
|
|
|
|
КНФ можно дать и другое равносильное определение. Формулу |
||||||
называют элементарной |
дизъюнкцией, если |
она |
является дизъюнкцией |
||||
(возможно, одночленной) переменных и отрицаний переменных. Формула находится в КНФ, если она является конъюнкцией (возможно, одночленной) элементарных дизъюнкций.
Вопрос №17. Совершенные нормальные формы.
Определение СДНФ. Пусть формула А зависит от n переменных. Говорят, что А находится в СДНФ относительно этих переменных, если выполняются следующие условия:
а) А находится в ДНФ (дизъюнкция элементарных конъюнкций);
12

б) в ней нет двух одинаковых дизъюнктивных членов (т.е.
элементарных конъюнкций); |
|
|
|
в) каждый |
дизъюнктивный |
член |
(элементарная |
конъюнкция) формулы А является n-членной конъюнкцией, причем на i-ом месте (1≤ i ≤ n) этой конъюнкции обязательно стоит либо переменная X i , либо еѐ отрицание X i .
Теорема. Пусть формула А зависит от списка переменных ( X1 , , X n ) и А не тождественно-ложная формула. Тогда существует такая формула В, что A B и В находится в СДНФ относительно списка этих переменных.
Доказательство. По теореме 6.2 существует формула A1 такая, что
и A1 находится в ДНФ. Пусть A1 зависит от списка переменных ( X1 , , X n ). Рассмотрим все еѐ элементарные конъюнкции:
1) |
Пусть в элементарную конъюнкцию одновременно входит какая- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
нибудь переменная X i и еѐ отрицание X i . Тогда X i X i Л. Если |
||||||||||||
|
эта элементарная конъюнкция единственная, то и вся формула А ≡ |
||||||||||||
|
Л, что невозможно … |
|
|
|
|
|
|
|
|||||
Следовательно, имеются другие элементарные конъюнкции: |
|||||||||||||
X i |
|
|
C D , где С – остальные члены элементарной конъюнкции, D – |
||||||||||
X i |
|||||||||||||
остальные дизъюнктивные члены всей формулы. |
|||||||||||||
|
|
|
|
|
X i |
|
C D D . Следовательно, |
||||||
Но поскольку X i X i C Л , то |
X i |
||||||||||||
рассматриваемую конъюнкцию можно отбросить. |
|||||||||||||
2) |
Пусть в некоторой элементарной конъюнкции переменная X i (или |
||||||||||||
|
|
|
|
||||||||||
|
|
X i ) встречается несколько раз. Тогда в силу идемпотентности |
|||||||||||
|
(равносильность 9) ... |
|
|
|
|
|
|
|
|||||
3) |
Далее возможны только следующие варианты: |
||||||||||||
а) элементарная конъюнкция D содержит один раз X i и не содержит ни разу X i ;
б) элементарная конъюнкция D содержит один раз содержит ни разу X i ;
в) элементарная конъюнкция D не содержит ни X i , ни X i .
В последнем случае заменяем D на D X i D X i по первой формуле расщепления (равносильность 19) (для выполнения условий а) или б)).
4)Переупорядочим в каждой элементарной конъюнкции еѐ члены так, чтобы на i-ом месте в ней стояла X i или X i .
5)Если в преобразованной формуле несколько раз встречается одна и та же элементарная конъюнкция, то, пользуясь равносильностью
13

10 (идемпотентность ), выбрасываем все еѐ вхождения, кроме одного.
Доказательство завершено.
Теорема о единственности СДНФ. Если B1 и B2 – СДНФ формулы А относительно списка переменных ( X1 , , X n ), то B1 и B2 могут отличаться только порядком своих дизъюнктивных членов.
Определение СКНФ. Пусть формула А зависит от n переменных. Тогда говорят, что А находится в СКНФ относительно переменных, если формула A* находится в СДНФ относительно тех же переменных.
Эквивалентное определение. Говорят, что А находится в СКНФ относительно списка переменных, если выполняются следующие условия:
а) А находится в КНФ (конъюнкция элементарных дизъюнкций); б) в ней нет двух одинаковых конъюнктивных членов (т.е.
элементарных дизъюнкций); в) каждый конъюнктивный член (элементарная дизъюнкция)
формулы А является n-членной дизъюнкцией, причем на i-ом месте (1≤ i ≤ n) этой дизъюнкции обязательно стоит либо переменная X i , либо еѐ отрицание X i .
Теорема. Пусть формула А зависит от списка переменных ( X1 , , X n ) и А не тождественно-истинная. Тогда существует такая формула В, что А В и В находится в СКНФ относительно списка этих переменных.
Доказательство первое. Пусть А уже находится в КНФ. По условию А на
каком-то наборе переменных принимает значение Л. Тогда A* на двойственном наборе принимает значение И и по теореме о СДНФ существует такая формула В1 , что A* B1 и В1 находится в СДНФ. По принципу двойственности В1* A и В1* находится в СКНФ.
Доказательство второе. Аналогично доказательству теоремы 6.4. При этом применяются равносильности Xi Xi C D D , D D Xi D Xi и законы идемпотентности (равносильности 9, 10). Доказательство завершено.
Теорема о единственности СКНФ. Если В1 и В2 – СКНФ формулы А относительно списка переменных ( X1 , , X n ), то B1 и B2 могут отличаться только порядком своих конъюнктивных членов.
Доказательство. При доказательстве можно воспользоваться принципом двойственности.
14
Теорема (критерий равносильности). Две формулы А1 и А2 , зависящие от одних и тех же переменных ( X1 , , X n ) и не равные тождественно Л (И), равносильны в том и только том случае, если они приводятся к СДНФ (СКНФ), отличающимся лишь порядком своих дизъюнктивных (конъюнктивных)
членов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
С одной стороны, если |
А1 и |
А2 |
|
приводятся к |
одной СДНФ |
В, то |
|||||||||||||
A1 B и |
A2 B . Следовательно, |
А1 A2 . |
|
|
|
|
|
|
|
||||||||||
С другой стороны, если A1 A2 |
и B1 |
– СДНФ для А1 , а B2 – СДНФ для А2 |
|||||||||||||||||
, то B1 A1 |
A2 , |
т.е. |
для формулы |
|
А2 |
будет 2 СДНФ: B2 и |
B1 . Тогда в силу |
||||||||||||
теоремы |
(6.5) |
B1 |
должна отличаться от B2 |
только |
порядком |
своих |
|||||||||||||
дизъюнктивных членов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Доказательство завершено. |
|
|
|
|
|
|
|
|
|||||||||||
Вопрос №18. Представление булевой функции формулой алгебры |
|||||||||||||||||||
высказываний. Таблицы истинности. |
|
|
|
|
|
|
|
||||||||||||
Определение. Булевой функцией f (x1, , xn ) |
называется произвольная п- |
||||||||||||||||||
местная функция, действующая из множества {0, 1} во множество {0, 1}. |
|
||||||||||||||||||
Представление булевой функции таблицей истинности. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число |
|
( |
) |
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
|
0 |
|
( |
) |
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
1 |
|
|
1 |
|
( |
) |
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
0 |
|
|
2 |
|
( |
) |
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
1 |
|
|
3 |
|
( |
) |
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
|
|
4 |
|
( |
) |
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
1 |
|
|
5 |
|
( |
) |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
0 |
|
|
6 |
|
( |
) |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
7 |
|
( |
) |
|
|
|
|
Лемма о числе слов. В алфавите A {a1, , ar } из r букв можно построить |
|||||||||||||||||||
ровно r m различных слов длины т. |
|
|
|
|
|
|
|
|
|||||||||||
Доказательство. Проведем индукцию по т. |
|
|
|
|
|
||||||||||||||
Пусть k m 1. Тогда получаем ровно r1 r слов длины 1. |
|
||||||||||||||||||
Пусть верно для |
k m 1, |
т.е. |
существует |
ровно |
r m 1 |
различных слов |
|||||||||||||
длины (т – 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для |
k m . |
Для каждого |
|
слова |
длины |
(m 1) |
существует ровно r |
||||||||||||
возможностей добавить одну букву в слово. В итоге получаем слова длины т, число которых равно rm .
Доказательство завершено.
15
Тогда по лемме 6.1 существует точно r m 22n различных п-местных булевых функций.
При п = 1 получаем 22n 221 4 булевы функции. При п = 2 получаем 22n 222 16 булевых функций.
Булева функция f (x1 , , xi 1 , xi , xi 1 , , xn ) существенно зависит от переменной xi , если существует такой набор значений 1, , i 1 , i 1, , n , что
f ( 1, , i 1,0, i 1, , n ) f ( 1, , i 1,1, i 1, , n ) .
В этом случае xi называют существенной переменной, в противном случае xi называют несущественной, или фиктивной переменной.
Теорема о разложении функции по переменным. Каждую булеву
функцию f (x1, , xn ) |
при любом k (1 ≤ k ≤ п) можно представить в следующей |
||||||||||||||
форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x , , x |
, x |
k 1 |
, , x |
) |
|
x 1 |
x k f ( |
, , |
k |
, x |
k 1 |
, , x |
) , |
||
1 |
k |
|
n |
( 1 |
, , k ) |
1 |
k |
1 |
|
|
n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где дизъюнкция берется по всевозможным наборам значений переменных x1, , xk .
Доказательство. Рассмотрим произвольный набор значений переменных ( 1 , , n ) и покажем, что левая и правая части соотношения принимают на нем одно и то же значение.
Левая часть
f (x1 , , xk , xk 1 , , xn ) f ( 1 , , n ) .
Правая часть
|
x 1 |
x k f ( |
, , |
k |
, x |
, , x ) |
|
( 1 , , k ) |
1 |
k |
1 |
|
k 1 |
n |
|
|
|
|
|
|
|
|
|
как только хотя бы один из сомножителей будет равен нулю, вся конъюнкция обратится в нуль. Таким образом, из ненулевых конъюнкций останется лишь та, в которой i i и
1 |
k |
f ( 1 , , n ) |
0 0 1 |
k |
всилу того, что 1, получаем
f ( 1, , n ) .
Доказательство завершено.
Следствие. Разложение произвольной булевой функции по одной переменной имеет вид
f (x1 , x2 , , xn ) x1 f (0, x2 , , xn ) x1 f (1, x2 , , xn ) .
Функции f (0, x2 , , xn ) и |
f (1, x2 , , xn ) называются компонентами |
разложения. |
|
16

Теорема о СДНФ булевой функции. Для любой булевой функции f (x1, , xn ) , отличной от константы 0, справедливо следующее представление
f (x , , x |
) |
|
x 1 |
x n |
|
1 |
n |
( 1 |
, , n ) |
1 |
n |
|
|
|
|
||
|
|
f ( 1 , , n ) 1 |
|
|
|
Такое разложение носит название совершенной дизъюнктивной нормальной формы булевой функции.
Теорема о СКНФ булевой функции. Для любой булевой функции f (x1, , xn ) , отличной от константы 1, справедливо следующее представление
|
|
|
|
|
|
|
|
|
f (x , , x |
) |
|
(x 1 |
x n ) . |
||||
1 |
n |
( 1 |
, , n ) |
1 |
n |
|||
|
|
|
|
|
|
|
||
|
|
f ( 1 , , n ) 0 |
|
|
|
|
|
|
Такое разложение носит название совершенной конъюнктивной нормальной формы булевой функции.
Вопрос №19. Алгебра Жегалкина.
Определение. Алгеброй Жегалкина называют алгебру на множестве булевых функций с двумя заданными операциями: конъюнкцией ( ) и суммой по mod 2 ( ).
В алгебре Жегалкина выполняются следующие равносильности:
1)x y y x (коммутативность );
2)x y y x (коммутативность );
3)x ( y z) (x y) z (ассоциативность );
4)x ( y z) (x y) z (ассоциативность );
5)x ( y z) (x y) (x z) (дистрибутивность относительно );
6)x x x (идемпотентность );
7)x x 0 ;
8)0 x 0 ;
9)0 x x ;
10)1 x x ;
11)x x 1;
12)x y (x y) (x 1) ( y 1) 1 x y x y .
Многочленом Жегалкина функции f (x1, , xn ) называется многочлен вида
n |
n |
P x1 ,..., xn a0 ai xi aij xi x j ... a12...n x1 x2 ... xn , |
|
i 1 |
i, j 1 |
|
i j |
где коэффициенты a0 , ai , aij , , a12...n принимают значение 0 или 1. |
|
Теорема Жегалкина. |
Каждая булева функция f (x1, , xn ) может быть |
представлена в виде многочлена Жегалкина и притом единственным образом, с точностью до порядка слагаемых.
17
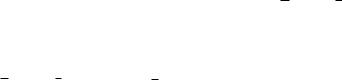
Пример. Пусть дана функция f (x, y, z) ( y ~ x) z . Рассмотрим два способа получения многочлена Жегалкина.
1 способ.
f (x, y, z) ( y ~ x) z [( y x) ( y x)] z
[( y x) ( y x)] z
…
(x y) z (x y) z x y z
(x z) ( y z) x y z
…
x z x y z y x y z 1
1 z xz yz P(x, y, z).
2 способ.
P(x, y, z) a0 a1x a2 y a3 z a12 xy a13xz a23 yz a123xyz f (x, y, z) ( y ~ x) z
|
|
|
̅ |
̅ |
|
̅ |
( |
) |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
0 |
P(0,0,0) a0 1 a0 |
1, |
|
|
|
|
|
|
|||
P(0,0,1) a0 |
a3 |
0, |
1 a3 |
0 a3 |
1, |
|
|
|||
P(0,1,0) a0 |
a2 |
1, |
1 a2 |
1 a2 |
0, |
|
|
|||
P(0,1,1) |
a0 a2 a3 |
a23 |
1, |
1 0 1 a23 |
1 a23 |
1, |
||||
P(1,0,0) a0 |
a1 |
1, |
1 a1 1 a1 0, |
|
|
|||||
P(1,0,1) |
a0 |
a1 a3 |
a13 |
1, |
1 0 1 a13 |
1 a13 1, |
||||
P(1,1,0) |
a0 |
a1 a2 |
a12 |
1, |
1 0 0 a12 |
1 a12 |
0, |
|||
P(1,1,1) a0 a1 a2 a3 a12 a13 a23 a123 0,
1 0 0 1 0 1 1 a123 0 a123 0,
Таким образом, P(x, y, z) 1 z xz yz.
Функция f (x1 , , xn ) называется линейной, если ее многочлен Жегалкина имеет вид
n
P(x1 , , xn ) a0 ai xi .
i 1
Вопрос №20. Дифференцирование булевых функций.
18
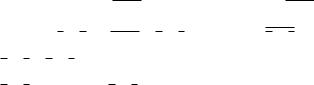
Производная |
первого |
порядка |
|
f |
от булевой функции f (x ,..., x |
) по |
||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
xi |
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
переменной xi есть функция |
|
|
|
|
|
|
|
|
|
|
||||||
|
f |
f x , x |
,..., x |
,1,..., x |
|
f x , x |
,...x |
,0,..., x |
|
, |
|
|
||||
|
|
|
n |
n |
|
|
||||||||||
|
xi |
1 2 |
|
i 1 |
|
1 2 |
|
i 1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
f x1, x2 ,..., xi 1,1,..., xn |
- единичная остаточная функция; |
|
|
||||||||||||
f x1 , x2 ,..., xi 1 ,0,..., xn - нулевая остаточная функция. Найдѐм производные функции: f a ~ b c.
fa
1 b c 0 b c 0 b c 1 b c
b c b c b c b c b c b c
b c b c b c b c
b c b c b c b c 1
|
f a ~ 1 c a ~ 0 c a ~ 1 |
a ~ c a a ~ c |
|
|
|||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||
f |
a ~ b 1 a ~ b 0 a ~ 1 a ~ b a a ~ b |
|
|
||||||||||||
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная первого порядка |
|
|
f |
|
от булевой |
функции |
f (x1 ,..., xn ) |
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
xi |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
определяет условие, при котором эта |
|
функция изменяет значение при |
|||||||||||||
изменении значения переменной xi |
и |
при неизменных |
других |
значениях |
|||||||||||
переменных ( |
f |
1). |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
0 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
1 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
1 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
0 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
0 |
0 |
|
1 |
|
|
0 |
0 |
|
1 |
|
|
0 |
1 |
1 |
|
|
0 |
1 |
|
0 |
|
|
0 |
1 |
|
0 |
|
|
1 |
0 |
1 |
|
|
1 |
0 |
|
1 |
|
|
1 |
0 |
|
1 |
|
|
1 |
1 |
1 |
|
|
1 |
1 |
|
0 |
|
|
1 |
1 |
|
0 |
|
|
19
