7. Пуск асинхронного двигателя

При пуске с началом разворота ротора двигатель должен преодолевать момент сопротивления рабочего механизма. Разгон двигателя происходит в соответствии с уравнением движения:

, (2.45)

при этом как момент двигателя М, так и момент сопротивления в общем случае являются функциями скорости .

В случае, когда 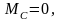и 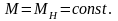показывает, что скорость нарастает равномерно и уравнение (2.45) принимает вид:

(2.46)

_{Определим, используя (2.46) время разгона двигателя при пуске до номинальной скорости}

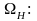
(2.47)

Найденное таким образом время t_н обозначают 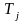- называют инерционной постоянной времени, здесь J -момент инерции ротора двигателя. Обычно определяют постоянную инерции для момента инерции

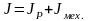
При сложных зависимостях и уравнение (2.45) аналитически не решается. Такое решение можно получить, используя интерполяцию момента двигателя для интервала скорости от до Ω = квадратичной функцией вида:

(2.48)

Аналогичное выражение зависимости момента сопротивления М_с(Ω) справедливо для многих судовых механизмов, таких как центробежные насосы, вентиляторы, гребные винты :

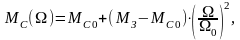(2.49)

здесь 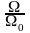- относительная величина скорости; 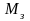- момент сопротивления загрузки механизма при скорости Ω ≈ Ω_Н.

Воспользуемся далее системой относительных единиц и перепишем уравнения (2.48) и (2.49), разделив их на номинальный базисный момент M_н. Учтем также, что отношение 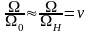- скорость (о.е), а μ -момент (о.е), тогда:

• для характеристики момента двигателя при скорости в пределах от 0 до запишутся как:

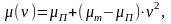(2.48,а)

• а характеристики момента сопротивления

(2.49,а)

Дифференциальное уравнение движения ротора для режима пуска примет вид:

Правую часть представим как произведение:

.

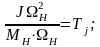
Итак, уравнение движения ротора в о.е.приводится к виду (2.48,а):

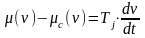(2.50)

Подставим (2.48,а) и (2.49,а) в левую часть (2.50) и введем обозначения:

(2.51)

С учетом введенных обозначений запишем:

• , если > 0 (2.52)

• , если ˂ 0 (2.53)

• в случае, если , то пуск оказывается невозможным.

Решение дифференциального уравнения движения (2.50) сводится таким образом к интегрированию (2.52) или (2.53). Разделяя переменные, имеем:

В случае пуска АД из неподвижного состояния нижний предел интегрирования равен нулю, а верхний ограничен критической скоростью:

(2.54)

В правой части (2.54) имеем табличный интеграл.

Его решение имеет вид:

если 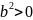(2.55)

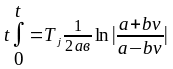если 0 (2.56)

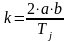
Обратные функции для (2.55) и (2.56) . т.е.зависимости , где (2.57)

(2.58)

8. Влияние различных параметров ад на переходный процесс пуска

На переходный процесс пуска АД влияют как параметры самого двигателя, так и величина напряжения.

Основным параметром, влияющим на процесс разгона двигателя и пусковые потери является активное сопротивление ротора Соотношение объясняется эффектом вытеснения тока к поверхности стержней при пусковой частоте 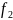тока в роторе, которая в момент пуска равна частоте сети 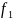; по мере же разгона уменьшается и эффект вытеснения пропадает. Этот эффект оказывает благоприятное действие на характеристики двигателя и, чтобы его усилить, применяют двигатели с повышенным вытеснением тока в стержнях ротора: роторы делают глубокопазными, бутылочными, двухклеточными, массивными.

При увеличенном сопротивлении ротора достигается большая величина пускового момента при меньшем пусковом токе . Такой двигатель быстрее разгоняется и меньше нагревается за время пуска. Однако в номинальном режиме он работает с большим скольжением и имеет увеличенные потери мощности (рис.2.7)

На рис.2.8 приведена характеристика тока 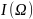и момента М(𝛺) двигателей одной и той же мощности и частоты вращения, но с разными сопротивлениями

Характеристики с индексом «1» относятся к АД продолжительного режима работы S1 с малым , а индексом «2» - к АД кратковременного режима работы S2 (или S3) с большим . Из сравнения точек пуска видно, что:

(2.59)

причем – это обусловлено единственно тем, что .

Увеличение критического скольжения 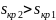обьясняется только увеличением , в соответствии с формулой

(2.60)

Отметим при этом, что величина самого максимального момента не зависит от сопротивления , и определяется выражением

(2.61)

Рис 2.8.- Характеристики момента и тока для двигателя продолжительного режима работы – характеристики 1, и для двигателя кратковременного режима работы – характеристики 2.

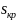Величина же номинального скольжения, ввиду практической линейности характеристики момента на ее рабочей (устойчивой) части, пропорциональна критическому скольжению. Таким образом, чем больше критическое скольжение , тем больше и номинальное скольжение 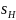(рис.2.8) величины преувеличены для большей наглядности.

, (2.62)

где μ_m =

Объясним, далее, почему в двигателях с повышенным сопротивлением при меньшем пусковом токе имеем больший пусковой момент > .

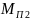Вращающий электромагнитный момент, определяется взаимодействием магнитного потока в воздушном зазоре и тока в роторе. Индукция магнитного поля в пределах полюсного деления 𝜏 распределена как полуволна синусоиды. Аналогично распределяются величины тока по стержням вдоль окружности воздушного зазора 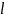. Однако, эти волны синусоид оказываются сдвинутыми в пространстве на некоторый угол 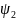, (рис. 2.9)

Рис.2.9.- Синусоиды распределения магнитной индукции и тока ротора вдоль окружности воздушного зазора

С учетом сдвига синусоид формула момента записывается как

M = Ф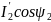 , (2.63)

где величина тем больше, чем больше , а соответственно угол тем меньше; называют также коэффициентом мощности роторной цепи, его величина определяется из схемы замещения вторичной цепи

(2.64)

При скольжении 𝘴 = 1,0, то есть в точке пуска имеет наименьшее значение

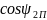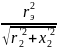= (2.65)

Несмотря на большой пусковой ток (в точке 𝘴 = 1.0) вследствие малого значения пусковой момент оказывается всего лишь чуть больше или чуть меньше номинального. При увеличении скорости ток падает, но быстрее при этом увеличивается 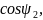(2.64), что приводит к увеличению момента. Момент достигает максимума в точке критической скорости (рис.2.8).

Для большинства проводов судовых центробежных насосов и вентиляторов применяют двигатели продолжительного режима работы S1. Эти двигатели имеют удовлетворительные пусковые свойства, но хорошие номинальные свойства.

Для приводов грузоподъемных механизмов, когда с первого же разворота ротора при пуске машине приходится преодолевать номинальный момент сопротивления, применяют двигатели режимов S2 и S3 (повторно-кратковременных режимов и режимов с частыми пусками). Эти двигатели имеют увеличенные значения сопротивления и повышенный момент при пуске, но работают хуже в установившемся режиме (по завершению пуска).