
2-й семестр / Лекция 11
.pdf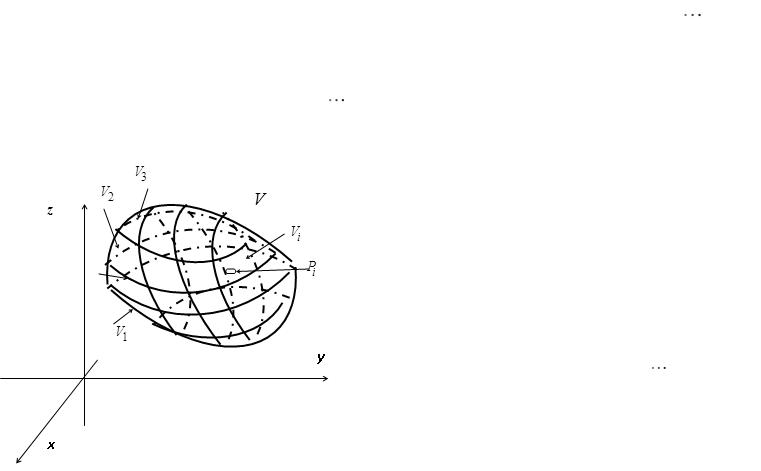
Тройной интеграл
Пусть в пространстве Oxyz задана ограниченная замкнутая область V, и пусть на области V опреде-
лена функция |
f (x, y, z) |
. |
|
Разобьём область V произвольным образом на |
n |
подобластей V1, V2, V3, |
,Vn (не имеющих общих внут- |
||||
|
|||||||
|
v(V ) |
|
|
|
V |
d |
|
ренних точек). Символом |
будем обозначать объём области |
i ; символом обозначим наибольший |
|||||
i |
|||||||
из диаметров областей
Vi
:
d
max |
diam(V |
|
i 1,2, |
,n |
i |
|
||
)
.
(Напомним, что диаметром ограниченной замкнутой области называется наибольшее расстояние между точками этой области и обозначается « diam ».)
чек
дела
В каждой из подобластей |
V |
(i 1,2,...,n) |
выберем произвольную |
i |
|
точку |
P |
(x , y , z ) |
, вычислим в этой точке значение |
функции |
||||||
i |
i |
i |
i |
|
||||||
|
|
|
|
|
|
|
n |
|
|
|
f (P ) f (x , y , z ) |
, и составим интегральную сумму |
|
f (P ) v(V ) |
|||||||
|
i |
i . |
||||||||
i |
|
i |
i |
i |
|
|||||
|
|
|
|
|
|
|
i 1 |
|
|
|
Определение Если существует
интегральных сумм при |
d |
max |
|
|
i 1,2, |
предел последовательности
diam(V ) 0 |
, не зависящий ни |
|
,n |
i |
|
|
|
|
|
от способа разбиения области V на подобласти |
V |
|||
|
i , ни от выбора то- |
||||
P |
f (x, y, z) |
называется интегрируемой по области V, а значение этого пре- |
|||
i , то функция |
|
||||
называется тройным интегралом от функции |
f (x, y, z) |
по области V и обозначается. |
|||
|
|||||
|
( ) = |
|
∑ ( ) |
|
|
|
|
→0 |
|
|
|
|
|
→∞ |
|
|
|
|
|
для |
|
|
|
или ( ) = (, , ) = |
|
∑ ( ) |
|||
|
|
|
|
→0 |
|
|
|
|
|
→∞ |
|
для
.
Относительно условий интегрируемости функции (, , ) справедлива точно такая же, как и в случае двойного интеграла, теорема:
Теорема. Если функция (, , ) непрерывна в ограниченной замкнутой области , то она интегрируема в этой области.
Непосредственно из самого определения тройного интеграла вытекает
Геометрический смысл тройного интеграла
Тройной интеграл от единичной функции (, , ) ≡ 1 по области V равен объёму этой области:
1 dv dv v(V ). |
|
V |
V |
(Действительно, в случае единичной функции (, , ) для любого разбиения области V интегральная
n
сумма v(Vi ) равна объему области V.)
i 1
Свойства тройного интеграла полностью аналогичны свойствам определённого и двойного интегралов, и основаны на свойствах предела функции.
Пусть в пространстве |
Oxyz |
задана ограниченная замкнутая область V. |
|
f
1. Линейность.
(P) g(P), P V,
Если функции |
f |
и |
g |
интегрируемы по области V, то их линейная комбинация |
|
|
|||
тоже интегрируема по области V и справедливо равенство: |
||||
f (P) g(P) dv f (P)dv g(P)dv . |
||||
V
V |
V |
2. Аддитивность. Пусть функция |
f |
интегрируема по области |
|
единением двух областей |
V |
и |
V |
, не имеющих общих внутренних |
1 |
2 |
|||
|
|
|
|
f (P)dv f (P)dv f (P) |
V. Тогда если область V |
является объ- |
точек, то справедливо равенство: |
|
dv |
|
. |
|
|
V |
V |
V |
|
|
1 |
2 |
3. Интегрирование неравенств. Если для интегрируемых по области V функций |
|||
точке P V |
выполняется неравенство |
f (P) g(P), то |
|
f и g
в любой
f (P)dv g(P)dv. |
|
V |
V |
4. Оценки интеграла. Если функция |
f интегрируема по области V, и |
m f (P) M , то справедливы оценки
m v(V ) f (P)dv M v(V ) .
V
P V
выполняется

5. Оценка модуля интеграла. Если функция интегрируема по области V и справедлива оценка:
f
интегрируема по области V, то функция
| |
f |
|
также
|
f (P)dv | f (P) | dv. |
||
|
V |
V |
|
Теорема о среднем. Если функция |
f непрерывна на области V, то существует точка |
||
что |
|
0 |
. |
|
|||
|
|
f (P)dv f (P ) v(V ) |
|
|
V |
|
|
P |
V |
0 |
|
, такая
Доказательство перечисленных свойств тройного интеграла проводится аналогично доказательству соответствующих свойств двойного интеграла.
2. Вычисление тройного интеграла в декартовых координатах. Сведение тройного интеграла к повторным
1). Будем называть ограниченную замкнутую область V простой (или правильной), если выполняются два условия:
-проекция V на какую-либо координатную плоскость, например, на плоскость Оху – некоторая замкнутая область D,
-любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку V, пересекает границу V в двух точках.
Такую область V можно представить следующим образом (см. рисунок):
V
(x, y, z) | (x, y) D,
(x, y)
z
(x,
y)
.
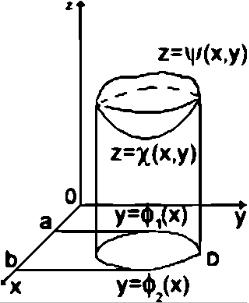
Таким образом, пространственная область V ограничена снизу поверхностью (которая образована множеством нижних точек пересечения прямых, параллельных оси Oz, с границей V), а сверху -
поверхностью |
z (x, y) |
(которая образована множеством верхних точек пересечения прямых, парал- |
|
лельных оси Oz, с границей V).
Теорема. Пусть V – замкнутая простая область с кусочно-гладкой границей (см. рис.), |
f (x, y, z) |
|||
|
||||
непрерывная функция в области V. Определим в области D следующую функцию: |
|
|||
|
|
(x, y) |
|
|
(x, y) D : |
I (x, y) |
|
f (x, y, z)dz. |
|
|
|
(x, y) |
|
|
Здесь в правой части стоит определенный интеграл по переменной |
z , внутри которого значения x и y |
фиксированы. Тогда справедлива формула: |
|
-
f (P)dv |
|
V |
D |
Если подставить в правую часть выражение для |
I |
|
|
ющий вид:
I (x, y (x, y)
) dxdy .
, то приведенная формула приобретает следу-
2( ) ( , )
(, , ) = ∫ |
(∫ |
(∫ |
(, , )) ) . |
||
|
|
1( ) |
( , ) |
|
|
|
|
|
|
|
|
|
|
(x, y) |
|
|
|
|
f (P)dv |
|
f (x, y, z)dz dxdy . |
||
|
|
|
|
|
|
|
V |
D (x, y) |
|
|
|
Однако традиционно эту формулу записывают в более удобном виде:
|
(x, y) |
|
|
|
f (P)dv dxdy |
|
f (x, y, z)dz |
(1) |
|
V |
D |
(x, y) |
|
|
|
|
|||
|
|
|
|
|
Интегралы, присутствующие в правой части этой формулы (внутренний одномерный и внешний двойной), называются повторными, а сама формула называется формулой сведения тройного интеграла к повторным.
Поясним, как проводится вычисление тройного интеграла по формуле (1).

Сначала находится внутренний определенный интеграл, в котором x и y рассматриваются |
как посто- |
|
янные значения, а переменной интегрирования является z. В таком случае первообразная для |
f (x, y, z) |
, |
|
||
обозначим ее через |
F(x, y, z) |
, будет зависеть только от z. Тогда, по формуле Ньютона-Лейбница, указан- |
|
ный внутренний определенный интеграл будет равен разности |
F(x, y, (x, y)) F(x, y, (x, y)) |
, тем са- |
|
мым, представлять собой функцию двух переменных x и y. Наконец, следуя формуле (1), находится двойной интеграл от этой функции по области D.
2). Предположим теперь, что область D в формуле (1) является простой плоской областью. В этом случае ее можно задать в виде (см. рис.):
D (x, y) | a x b, 1(x) y 2(x) .
Тогда, представляя внешний двойной интеграл в формуле (1) в виде повторных (см. лекцию о двойном интеграле), получаем ещё более детализированную формулу для вычисления тройного интеграла:
2( ) ( , )
(, , ) = ∫ |
(∫ |
(∫ |
(, , )) ) . |
|
|
|
1( ) |
( , ) |
|
|
|
|
|
|
|
(x, y) |
b |
2 (x) |
(x, y) |
|
||
f (P)dv dxdy |
|
f (x, y, z)dz dx |
|
dy f (x, y, z)dz |
(2) |
||
V |
D |
(x, y) |
a |
|
1(x) |
(x, y) |
|
3). Тройной интеграл также можно представить в виде повторных интегралов с иным, чем формулы (1), порядком интегрирования. Для этого область V проектируется на плоскость Oxz или на плоскость Oyz. D – проекция области на одну их этих плоскостей.
4). Если область V – сложная, то ее разбивают на конечное число простых областей (проекция каждой простой области на одну из координатных плоскостей однозначна). Далее используется свойство аддитивности тройного интеграла.
5). При переходе к повторным интегралам необходимо следить, чтобы пределы интегрирования не содержали ту переменную, по которой ведется интегрирование. Внешние пределы интегрирования – константы.
Пример. Вычислим интеграл ,
где – треугольная пирамида с вершинами в точках (0,0,0), (15,0,0), (0,10,0) и (0,0,6).
Ее проекцией на плоскость является треугольник с вершинами (0,0), ( , ) и ( , ). Снизу область ограничена плоскостью = 0, а сверху – плоскостью 2 + 3 + 5 = 30. Перейдем к трехкратному интегралу:

z2

