2-й семестр / Лекция 11
.pdf
5. Тройной интеграл в сферических координатах
1). Сферические координаты вводятся во всем трехмерном пространстве Охуz. В этой координатной
системе положение произвольной точки |
M M(x, y, z) |
в пространстве характеризуется тройкой чисел |
|
r, , |
|
|
|
|
, которые имеют следующий смысл: |
|
|||
r – это длина радиуса-вектора точки M |
|
|||
|
– угол между радиусом-вектором точки M и осью Oz |
|||
|
||||
– полярный угол точки N, являющейся проекцией точки M на плоскость Оху. |
||||
|
||||
|
z |
M(x,y,z)=M( |
) |
|
r
O |
y |
|
r sin
x 
N
Формулы перехода от сферических координат к декартовым координатам имеют вид:
= { = =
Вычислим якобиан перехода от сферических координат к декартовым:
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|||||||
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
| |
|
|
|
|
| |
| |
|
|
|
|
|
|
|
|
|
|
| |
|||||
(, , ) = |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
| |
|
|
|
| |
| |
|
|
|
|
|
|
|
|
|
|
| |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
− |
|
= | |
|
|
| = 2 ∙ | |
|
| = |
|
|
− |
|
0 |
|
− |
0 |
|
|
|
Разложим определитель |
|
|
|
|
|
= | по третьей строке |
| = |
|
|
|
|
|
|
находим |
|
|
|
= ( 2 + |
2 ) + ( 2 + 2 ) = 1. |
|||||
Окончательно получаем, что
J (r, , ) r |
2 |
sin |
|
||
|
|
|
Следовательно, формула (4) замены переменных в тройном интеграле в случае сферических коорди-
нат принимает следующий вид:
(, , ) = (, , ) 2
|
|
для любой непрерывной функции
f (x,
Здесь G – область в пространстве пространстве Oxyz.
y, z) |
|
в области V. |
|
Or |
сферических координат |
|
|
r, ,
, отвечающая области V в
Замечание. К сферическим координатам удобно переходить, если область V – шар или часть его, или подынтегральная функция имеет вид (2 + 2 + 2). В сферических координатах 2 + 2 + 2 = 2.
Приложения двойного и тройного интегралов
Пример 2. Вычислить тройной интеграл по области V, ограниченной указанными поверхностями:
Решение. Проведем несколько последовательных шагов.
Переобозначим координатные оси. Перейдем к сферическим координатам.
Найдем пределы интегрирования, то есть интервалы изменения сферических координат: изменяется
от оси Oz до поверхности конуса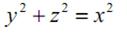 
, которая в сферических координатах имеет вид:
Это полукруг с центром в начале координат. Поскольку по условию > 0, значит, угол меняется в пределах от 0 до .
3) Ясно, что r меняется в пределах от 0 до R .
и находим данный интеграл, сведя его к повторному:
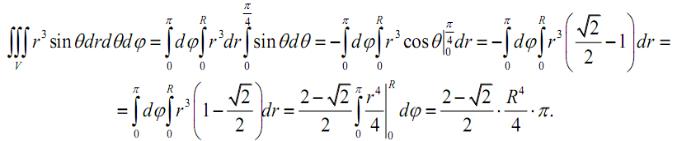
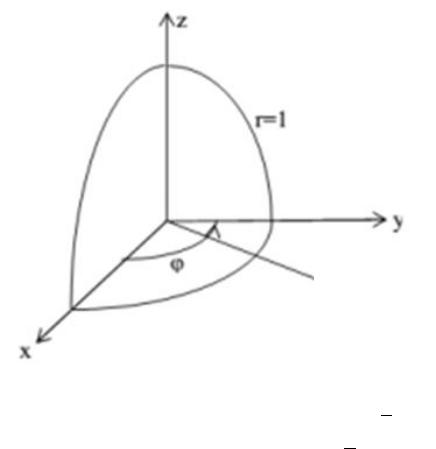
Пример 2. Вычислить ,
где V – часть шара
2 + 2 + 2 ≤ 1, лежащая в 1 октанте
( ≥ 0, ≥ 0, ≥ 0).
Проекцией области V на плоскость Oxy является часть круга, лежащего в 1 четверти, поэтому 0 ≤ ≤ 2.
Для всех точек шара ≤ 1. 0 ≤ ≤ 2.
= 2 =
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
1 |
2 |
|
|
2 |
|
|
6 1 |
4 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
2 |
1 |
|
1 |
|
1 |
|
1 |
|||||||||||
= ∫ ∫ 5 |
∫ 3 |
|
|
|
|
|||||||||||||||||
= |
|
|
| |
∙ |
|
| ∙ |
|
| |
= |
|
|
∙ |
|
|
∙ |
|
= |
|
||||
2 |
|
6 |
4 |
2 |
6 |
4 |
48 |
|||||||||||||||
0 |
0 |
0 |
|
|
|
|
0 |
0 |
|
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Приложения интегралов
|
определенный интеграл |
двойной интеграл |
тройной интеграл |
||||
|
|
|
|
|
|
|
|
1. |
∫ = [ , ] |
= ( ) |
|
= |
|||
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
∫ ( ) = |
(, ) = |
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ ( ) = |
|
|
|
|
||
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
масса |
|
масса |
|
масса |
|
|
( ) |
|
|
||||
4. |
= стержня |
(, ) = плоской |
= тела |
||||
∫ |
|||||||
|
|
|
|
пластины |
|
объема |
|
|
|
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
5. |
|
|
|
статический |
|
статический |
|
|
|
|
( ) |
= моментМх |
= моментМх |
||
|
|
|
, |
||||
|
|
|
|
относ. оси Ох |
|
отн. пл. Ох |
|
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|