
- •27. Взаємне розташування прямої і площини у просторі
- •34.Неперервність ф-ції. Властивості неперервних ф-цій. Точки розриву ф-цій та їх класифікація.
- •35. Задачі, що приводять до поняття похідної. Означення похідної. Її геометричний та механічний зміст.
- •36 Правила диференціювання
- •43. Основні поняття та означення функції багатьох змінних.
- •51. Первісна ф-ція. Невизначений інтеграл
- •52. Таблиця невизначених інтегралів. Безпосереднє інтегрування виразів.
- •53. Метод підстановки та інтегрування за частинами.
- •54 Інтегруваня раціональних дробів
- •55 Інтегр навпрост ірац фцій
- •56 Визн інтеграл ,
- •57 Обчисл визн інтегралу ,форм Нютона –лейбніца
- •58 Обч площ плоскіх фігур
- •59 Обчисленняоб’ємутілаобертання
1. Математика. зв’яз. мат з економ. Математика – це наука про кількісні співвідношення, структури, форми та перетворення. Розділи: 1. Арнометика,2.геометрія 3. алгебра. Курс вищої математики розглядає системний аналіз який викор. для розв’язання ек. задач на знаходження продуктивності праці обчислення прибутку та витрат що пов’язані з виробництвом.
2.економіко-математичне мод- елювання. Задача планування виробниц- тва. Еконо́міко-матем. моде́лі — моделі ек. об'єктів або процесів, при описі яких використовуються математичні засоби. Цілі створення економіко-математичних моделей різноманітні: вони будуються для аналізу тих чи інших передумов і положень економічної теорії, логічного обгрунтування ек. закономірностей, обробки і приведення в систему емпіричних даних. Економіко-математичні моделі створюються і вивч. оскільки проводити експерименти з економікою дуже складно, а часто і просто неможливо. При відсутності попереднього аналізу ек. ситуації такі експерименти можуть призвести до негативних наслідків (як ек., так і соціальних).
3. Поняття матриці. Задачі які приводять до матриці. Застосув. матриці в економ розрах. Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця) і допускаючий операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми.Матриці є корисними для запису даних, що залежать від двох категорій, наприклад: для коефіцієнтівсистем лінійних рівнянь та лінійних перетворень.
4. Види матриці. Дії над матрицями елементарні перетвор знаходження рангу матриці. Види матриці: 1. Матриця рядка 2.Матриця стовбця. 3.квадратна мат-ця. 4. Трикутна мат-ця.5.Діагональна мат-ця. 6. Одинична мат-ця. Дії над матр-ми: 1.Транспортування-поляг у заміні відповідного рядка стовпцем. 2. (Додавання- віднімання) – викнується якщо мат-ці однакового порядку при цьому відповід елементи додаються. 3. Множення мат-ці на скаляр – при цьому кожен елемент мат-ці множиться на дане число. 4. Множення- дана дія викон якщо к-ть стовпців 1-ї мат-ці = к-ті 2-ї мат-ці при цьому відповід рядки перемнож і додаються до відповід стовпців. Ранг матриці — це розмірність образалінійного відображення, представленого матрицею. Вона збігається з розмірністю простору, згенерованого рядками матриці, а також із розміром простору, згенерованого стовпчиками матриці .
|
5. Визначник 2-го і 3-го порядку. Обчисл. визначників n-го порядку. Властивості визначників. Розкалд визначників за елемент рядків та стовпців. Визначник— одна з найважливіших характеристик квадратних матриць. Визначник 2-го порядку -Щоб знайти визначник 2-го прядкум, множимо елементи головної діагоналі та віднімаємо добуток елементів побічної діагоналі. При обчисленні визначника 3-го порядку використовується три способи: 1. Розкладання за елементами довільного рядка. 2. Метод трикутників. Властивості визначника: 1. Визначник не зміниться у результаті транспортування матриці. 2.Якщо один із рядкив виз-ка склад лише з нулів то такий виз-к дорівнює нулю.3. якщо помін місцями будь-яких два рядки стовпців то його знак зміниться на протилежний. 4.виз-ник який має два однакових рядки дорівнює нулю. 5. Якщо всі елементи будь-якого рядка(стовпця) помножити на стале число то і виз-ник помножиться на це число. 6. Виз-ник не змінюється якщо до елементів будь-якого рядка(стовпця) додати відповідні елементи довільного іншого рядка попередньо помноженого на деяке число. Елементи визначника:1. Мінор – це визначник (м) в -1 степені порядку який отримуємо у результаті ви креслення відповідного рядка і стовпця. 2. Алгебраїчні доповнення – мінор який взятий зі знаком.
6-питання. Обернені матриці. Матриця
|
7-питання. Система лінійних алгебраїчних рівнянь. Система трьох рівнянь (3 площини) з трьома невідомими (тривимірність простору). Розв'язком є точка перетину площин. Система лінійних алгебраїчних рівнянь (СЛАР) — в лінійній алгебрі це система лінійних рівнянь виду:
Це система m лінійних рівнянь з n невідомими, де
Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задач лінійної алгебри, теорії диференціальних рівнянь, математичної фізики, тощо, та областей фізики й техніки, де застосовуються ці математичні теорії.
де A — матриця m×n, x — вектор з n компонент, b — вектор з m компонент.
Число векторів в базисі лінійної оболонки векторів є рангом матриці. Розв’язком
системи лінійних алгебраїчних рівнянь
є будь-яка сукупність дійсних
чисел Якщо система має хоча б один розв’язок, то вона називається сумісною, і несумісною, якщо не має жодного. Відповідь на питання сумісності системи дає теорема Кронекера-Капеллі. Сумісна система називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо вона має безліч розв’язків. В останньому випадку кожен її розв’язок називають частковим розв’язком системи. Сукупність усіх часткових розв’язків називають загальним розв’язком системи. Якщо
всі вільні члени
|
|||
8-питання.метод обчислення виз-ків. Обч. визначника третього порядку можна здійснювати за правилом трикутників:або правилом правилом Саррюса:у початковому визначнику за третім стовпцем запишемо ще раз перший і 2ий стовпці:Методом многочленів зручно обч. визначники матриць, які міс-тять велику к-сть нульових елементів. Він безпосередньо випливає з означення визначника як числового множника в добутку чисел Грассмана, що відповідають рядкам визначника. Метод
Крамера (Крамера правило)
— спосіб розв'язання квадратних систем
лінійних алгебраїчних рівнянь
із ненульовим визначником
основної матриці (при цьому для таких
рівнянь розв'язок існує і є єдиним).
Метод було створено Габріелем
Крамером
у 1750
році…Для
системи
з
визначником матриці системи
9-питання.матричний метод розв*яз системних рівнянь Метод розв’язання систем лінійних алгебраїчних рівнянь заданих матричним способом. Якщо — основна матриця системи,
то
має місце рівність: Якщо
матриця
є
квадратною
та невиродженою,
то для неї існує обернена
матриця. Помноживши обидві частини
рівняння зліва на
оскільки
|
10-питання.Розвяз сист рівнянь методом гауса , гауса –жордана. Ме́тод Га́уса — алгоритм розв'язку системи лінійних алгебраїчних рівнянь. Початок
алгоритму. Прямий хід: Шляхом елементарних перетворень рядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться до верхньотрикутного вигляду.З цього моменту починається зворотний хід.З останнього ненульового рівняння виражаємо кожну з базисних змінних через небазисні і підставляємо в попередні рівняння. Повторюючи цю процедуру для всіх базисних змінних, отримуємо фундаментальний розв'язок. Метод Гауса— Жордана використовується для розв'язання систем лінійних алгебраїчних рівнянь, знаходження оберненої матриці, знаходження координат вектора у заданому базисі, відшукання рангу матриці. Метод є модифікацією методу Гауса. Названий на честь Гауса та Жордана(рус.).
11-питання.предмет і метод аналіт геометрії. Аналітична геометрія і векторна алгебра це розділ у якому розгляд. Геометри. Співвідношення за допомогою методів алгебри. Предметом вивчення аналітичної геометрії є вивчення геометрич-них образів алгебраїчними методами. Основні поняття: рівняння пряої і площини ,поняття вектора. Аналітична геометрія базується на декартовій системі координат. Основоположником декартової системи координат на площині є Ферман і Декат. Основні задачі аналітичної геометрії: знаходження відстані між двома точками /АВ/=корінь ( хв.-ха^)2 +(yв-уа)^2;поділ відрізка у заданому відношенні /AC:СВ/=лямда;обчислення площі трикутника. 12.застосув. методів аналітичної геометрії Методи аналітичної геометрії використовуються для розв’язання задач лінійного програмування ,що є основою моделювання виробництва чи знаходження оптимального розв’язку. Приклади задачі :1)транспортна; 2) задача раціонального розкрою матеріалів.
13 14.15 Загальне рівняння прямої Ах+Ву+С=0 У просторі Ах+Ву+Сz+Д=0 А і В – це координати нормального вектора.Векторне рівняння прямої А(х-х0)+В(у-у0)=0 Каонічне рівняння прямої (х-х0)/m=(у-у0)/n. Рівняння прямої з прямими коефіцієнтами y-уа=k(х-Ха) Рівняння прямої через дві точки х-х1/х2-х1=у-у1/у2-у1 Прямі на площині можуть :1) перпендикулярними(під довільним кутом , або 90) 2) не перетинатись (паралельні або мимобіжні) Якщо прямі перетинаються ,то кут між двома прямими соs =А1А2+В1В2/Корінь А1А2^2+В1В2^2
|
16-питання.кут між прямими. Відстань від точки до прямої — = довжині перпендикуляра, опущеного з точки на пряму.
17-питання.знаход відстані між 2-ма точками. Ві́дстань між двома́ то́чками — довжина уявного відрізка, кінцями якого є ці точки. Найкоротший шлях, яким можна дістатися з однієї точки в іншу. В аналіт. геометрії відстань між2ма точк A(x1, y1) і B(x2, y2) на площині можна зн. за формулою
Якщо
позначити різницю
(x2
- x1)
як
У тривимірному просторівідстаньміжточками знаходиться майже так само:
18-питання. Вектори. Векторні простори Вектором
називається напрямлений відрізок.
Вектори
|
19-питання. Координати векторів
Вид прямокутної системи координат на площині показано на рисунку. Пряму x називають віссю абсцис, пряму у – віссю ординат. Кожній точці площини відповідають два числа (координати).На першому місці записують координату по осі х (інакше - абсцису), на другому – координату по осі у (інакше - ординату).Координатами вектора a називають числа a1 = x2 - x1, a2 = y2 - y1,де A1(x1, y1), A2(x2, y2) - кінці вектора a.Рівні вектори мають рівні відповідні…….координати.Якщо у векторів координати рівні, то вектори рівні.
Дії
з векторами, заданими в координатній
формі.Правило множення вектора на
число.Щоб помноживши вектор
![]() на
число k, треба усі координати вектора
помноживши на число k, тобто k
=
на
число k, треба усі координати вектора
помноживши на число k, тобто k
=
![]() Правилознаходження
алгебраїчної суми векторів.
Правилознаходження
алгебраїчної суми векторів.
Координати алгебраїчної суми скінченної кількості векторів дорівнюють такій же алгебраїчній сумі відповідних координат цих векторів.Так, у випадку алгебраїчної суми трьох векторів:
![]() ,
,
![]() ,
,
![]() їх
алгебраїчна сума
їх
алгебраїчна сума
![]() знаходиться
за формулою
знаходиться
за формулою
=![]()
20-питання. Скалярний добуток векторів
Скалярний
добуток —
математ.
операція над 2ма
векторами.
Cкалярний добуток векторів
![]() та
та
![]() обчислюється
за формулою:
обчислюється
за формулою:![]() де
де
![]() та
та
![]() є
довжинами
векторів, а
є
довжинами
векторів, а
![]() дорівнює
косинусу
кута між цими векторами. Як і у випадку
звичайного множення,
знак множення можна не писати:
дорівнює
косинусу
кута між цими векторами. Як і у випадку
звичайного множення,
знак множення можна не писати:
![]() =
=
![]() .
.
Два означення добутку векторів.
Скалярним добутком двох векторів - називається число, рівне добутку довжин цих векторів на косинус кута між ними.
Скалярним добутком двох векторів - називається число, рівне добутку довжини одного з цих векторів на проекцію іншого вектора на вісь, обумовлену першим з вказаних векторів.
В
лінійній
алгебрі поняття скалярного добутку
узагальнено. Так, скалярним добутком
називається функція, що зіставляє парі
елементів векторного
простору елемент з поля,
над яким побудований векторний простір.
Скалярний добуток двох векторів
та
![]() позначається
як
позначається
як
![]() .
Можлива і скорочена форма запису:
.
Можлива і скорочена форма запису:
![]() .
Також можливе позначення
.
Також можливе позначення
![]() ,
що підкреслює зв'язок з множенням
матриць.
,
що підкреслює зв'язок з множенням
матриць.
Взагалі кажучи, для векторного простору існують різні варіанти скалярного добутку. Простір із визначеним скалярним добутком позначається як прегільбертів простір.
Кутом між двома векторами, відкладеними від однієї точки, називається найкоротший кут, на який потрібно повернути один з векторів навколо свого початку до положення співнаправленості з іншим вектором.
Косинус кута між векторами дорівнює скалярному добутку векторів, поділеному на добуток модулів векторів.
Формула обрахунку кута між векторамиcos α = |
a·b |
|a|·|b| |
21-питання. Лінії 2го порядку. Канонічне рівння кола та еліпса
Лінії другого порядку — геометричне місце точок на площині, декартові координати яких задаються рівнянням другого степеня:
![]()
де
хоча б один з коефіцієнтів
![]() відмінний
від нуля.
відмінний
від нуля.
Канонічне рівняння еліпса. Нехай на площині взято прямокутну систему координат Оху (рис.15) і нехай точки F1іF2з координатами (-с;О) і (с;О) відповідно - фокуси еліпса. Якщо М(x,y) - довільна точка еліпса, то, згідно з означенням еліпса, виконується рівність

Канонічне
рівння кола
Виведемо рівняння кола. Нехай: М(х,
у)
довільна точка кола; О(а,
b) –
його центр і R
-
радіус. Ізвизначення кола запишемо
співвідношення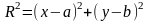 ,
,
22-питання. Лінії 2го порядку. Канонічне рівняння гіперболи
Лінії другого порядку — геометричне місце точок на площині, декартові координати яких задаються рівнянням другого степеня:
де хоча б один з коефіцієнтів відмінний від нуля.
Канонічне рівняння гіперболи. Нехай на площині узято прямокутну декартову систему координат Оху (рис. 16), і нехай точки F1(-c;O) і F2(c;O) - фокуси гіперболи. Множина точок М(х,у), які утворюють гіперболу згідно з означенням гіперболи, задовольняє рівняння
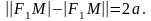
23-питання Лінії 2го порядку. Канонічне рівняння параболи
Лінії другого порядку — геометричне місце точок на площині, декартові координати яких задаються рівнянням другого степеня:[1]
де хоча б один з коефіцієнтів відмінний від нуля.
Канонічнерівняння
параболи. Нехай на площині узято
прямокутну декартову систему координат
Оху,
і
нехай точка F
з координатами (p/2;
0)
-
фокус параболи, а пряма, задана рівнянням
х
= –р/2, -
директриса параболи (рис.17). Координати
будь-якої точки М(x,
y),
яка належить параболі, задовольняють
рівняння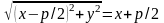 .
.
24-пит. Прямокутна декартова система
Прямокутна
система координат у просторі
утворюється трьома взаємно перпендикулярними
осями координат O
X
, O
Y
і O
Z
. Осі координат перетинаються в точці
O
, Яка називається початком координат,
на кожній осі вибрано позитивне напрямок,
вказаний стрілками, і одиниця виміру
відрізків на осях. Одиниці виміру
зазвичай однакові для всіх осей (що не
є обов'язковим). O
X
- вісь
абсцис,
O
Y
- вісь
ординат,
O
Z
- вісь
аплікат.
Якщо великий палець правої руки взяти
за напрям X
, Вказівний за напрям Y
, А середній за напрям Z
, То утворюється права
система координат. Аналогічними пальцями
лівої руки утворюється ліва система
координат. Інакше кажучи, позитивний
напрям осей вибирають так, щоб при
повороті осі O
X
проти годинникової стрілки на 90 її
позитивний напрям співпало з позитивним
напрямом осі O
Y
, Якщо цей поворот спостерігати зі
сторони позитивного напрямку осі O
Z
. Праву і ліву системи координат неможливо
поєднати так, щоб збіглися відповідні
осі.Положення
точки A
в просторі визначається трьома
координатами x
, y
і z
. Координата x
дорівнює довжині відрізка O
B
, Координата y
- Довжині відрізка O
C
, Координата z
- Довжині відрізка O
D
у вибраних одиницях виміру. Відрізки O
B
, O
C
і O
D
визначаються площинами, проведеними з
точки A
паралельно площинам Y
O Z
, X
O Z
і X
O Y
відповідно. Координата x
називається абсцисою точки A
, Координата y
- Ординатою точки A
, Координата z
- аплікат
точки A
. Записують так:
![]()
25-питання. Заг рівння площини у просторі
Загальне
(повне) рівняння площини![]() де
де
![]() та
та
![]() —
сталі, при чому
—
сталі, при чому
![]() і
і
![]() не
всі рівні нулю; у векторній
формі:
не
всі рівні нулю; у векторній
формі:![]() де
де
![]() —
радіус-вектор точки
—
радіус-вектор точки
![]() ,
вектор
,
вектор
![]() перпендикулярний
до площини (нормальний
вектор). Напрямні
косинуси
вектора
перпендикулярний
до площини (нормальний
вектор). Напрямні
косинуси
вектора
![]() :
:![]()
![]()
![]() Якщо
один з коефіцієнтівв
рівнянні площини дорівнює нулю рівняння
називаєтся неповним.
При
Якщо
один з коефіцієнтівв
рівнянні площини дорівнює нулю рівняння
називаєтся неповним.
При
![]() площина
проходить через початок
координат,
при
площина
проходить через початок
координат,
при
![]() (або
(або
![]() ,
,
![]() )
площина паралельна осі
)
площина паралельна осі
![]() (відповідно
(відповідно
![]() чи
чи
![]() ).
При
).
При![]() (
(![]() ,
чи
,
чи
![]() )
площина паралельна площині
)
площина паралельна площині
![]() (відповідно
(відповідно
![]() чи
чи
![]() ).
).
26-питання
Двогранний кут між площинами дорівнює куту утвореному нормальними векторами цих площин.Двогранний кут між площинами дорівнює куту утвореними прямими l1 і l2, що лежать в відповідних площинах і перпендикулярні лінії перетину площин.Якщо задані рівняння площин A1x+ B1y+ C1z+ D1 = 0 і A2x+ B2y+ C2z+ D2 = 0, то кут між площинами можна знайти, використавши наступну формулу
cos α= |
|A1·A2 + B1·B2 + C1·C2| |
(A12 + B12 + C12)1/2(A22 + B22 + C22)1/2 |
27. Взаємне розташування прямої і площини у просторі
Якщо дві точки прямої належать площині, то за аксіомою СII всі точки прямої належать площині, або, інакше кажучи, вся пряма належить площині. Пряма і площина можуть мати одну спільну точку або не мати спільних точок взагалі. Отже, можливі три випадки розміщення прямої і площини:
1) пряма належить площині (мал. 372).
2) пряма і площина мають одну спільну точку, тобто перетинаються (мал. 373).
3 )
пряма і площина не мають спільних точок
(мал. 374).
)
пряма і площина не мають спільних точок
(мал. 374).
28. Рівняння прямої у просторі. Кут між двома прямими
У просторі Ах+Ву+Сz+Д=0 А і В – це координати нормального вектора
кут між двома прямими соs =А1А2+В1В2/Корінь А1А2^2+В1В2^2
29-питання. Поняття множини, ф-ції, послідовності.
Множиною функції назив. – сукупність елементів які об’єднана певною ознакою.
Послідовністю назив. – сукупність чисел або об’єктів які записані у певному порядку.
Функція – це числова відповідність коли кожному значенню (Х) відповідає єдине значення (У).
y=f(x)
Види фун-ій: 1. Парні і не парні
f(-x) = f(x) if(-x)=-f(x)
2.періодична і не періодична.
F(x+t) = f(x) t – періодичність
3. Буває обмеженою на проміжку і не обмеженою.
4. Є зростаюча складна
30-питання. Способи заданя ф-ції
Елементарні функції
Основні з них:
1) степенева у = ха;
1) степенева у = ха;
2)
показникова у = ах, а > 0, а
![]() 1
1
3) логарифмічна у = logа х, а > 0, а 1
4) тригонометричні: у = cosx; у = sinx у = tgx ; у = ctgx ;
5) обернені тригонометричні: y = arcsinx; y = arccosx; у = arctgx; у = arcctgx
31-питання. Нескінченно малі та великі велечини
Нескінченно малі величини найчастіше позначають літерами α,β,γ.
Нескінченно
мала величина є змінною величиною. Але,
якщо постійну величину О розглядати як
змінну величину, що приймає одне й те ж
значення, то в цьому розумінні вона є
нескінченно малою, тобто якщо α=0, то
нерівність |а|<![]() виконується для будь-якого
>
О,Жодну іншу постійну величину, якою би
малою вона не була (наприклад, розмір
електрона), не можна назвати нескінченно
малою.Теорема 1. Алгебраїчна сума
будь-якого скінченного числа нескінченно
малих величин є величина нескінченно
мала.
виконується для будь-якого
>
О,Жодну іншу постійну величину, якою би
малою вона не була (наприклад, розмір
електрона), не можна назвати нескінченно
малою.Теорема 1. Алгебраїчна сума
будь-якого скінченного числа нескінченно
малих величин є величина нескінченно
мала.
Доведення.
Нехай задано k нескінченно малих величин
α1, α2,...,αk. Доведемо, що їх алгебраїчна
сума (α1 ± α2 ± ... ± αk) буде величиною
нескінченно мстою. Змінна
величина х називається нескінченно
великою,
якщо а процесі її зміни наступиш такий
момент, починаюча з якого абсолютна
величина х стає і залишається більше
будь-якого, скільки завгодно великого,
наперед заданого додатного числа N,
тобто
![]() >N.Між
нескінченно великими і нескінченно
малими величинами
існує простий зв'язок: якщо х нескінченно
велика величина, то
>N.Між
нескінченно великими і нескінченно
малими величинами
існує простий зв'язок: якщо х нескінченно
велика величина, то
![]() —
нескінченно мала, і навпаки, якщо у —
нескінченно мала і у
—
нескінченно мала, і навпаки, якщо у —
нескінченно мала і у![]() 0,
то
0,
то
![]() буде
нескінченно великою величиною.
буде
нескінченно великою величиною.
32-питання. Границі послідовності
Границя послідовності. Основні теореми про границі. Обчислення границь.
Границя- Lim хn=a (n -∞)
Число а є границе ю послідовності хн при n -∞ , якщо для будь-якого Ебільше0 існує N,що для всіх nбільше N виконується нерівність /Х n-а/більше Е
Теорема Вайерштраса Якщо послідовність монотонна і обмежена то вона має границю.
Теореми про границі
Алгебраїчна сума двох збіжних послідовностей і є збіжна послідовність, її границя дорівнює відповідній сумі границь даних послідовностей.
![]()
Добуток двох збіжних послідовностей і є збіжна послідовність, її границя дорівнює добутку границь даних послідовностей.
Наслідок 1. Якщо послідовність має скінчену границю, то при всякому сталому маємо:
![]() або
сталий множник можна виносити за знак
границі.
або
сталий множник можна виносити за знак
границі.
Наслідок
2. Якщо і - натуральне число,то
![]()
Якщо послідовності і збігаються, причому і то послідовність збігаються і її границя дорівнює відношенню границь послідовностей
33-питання. Границя ф-ції
Нехай
функція
![]() визначена
у всіх точках проміжку
визначена
у всіх точках проміжку
![]() ,
за винятком, можливо, деякої точки
,
за винятком, можливо, деякої точки
![]() .
Побудуємо послідовність значень
аргументу функції
:
.
Побудуємо послідовність значень
аргументу функції
:![]() ,
,
![]() ,
таку, щоб всі члени послідовності
належали проміжку
і
послідовність збігалась до точки
,
таку, щоб всі члени послідовності
належали проміжку
і
послідовність збігалась до точки
![]() :
:![]() .Тоді
значення функції
.Тоді
значення функції
![]() .
також утворять деяку числову
послідовність.Говорять, що число
.
також утворять деяку числову
послідовність.Говорять, що число
![]() є
границею функції
при
є
границею функції
при
![]() ,
що прямує до
,
якщо для будь-якої послідовності значень
аргументу , яка збігається до числа
,
послідовність значень функції (2)
збігається до числа
,
і пишуть
,
що прямує до
,
якщо для будь-якої послідовності значень
аргументу , яка збігається до числа
,
послідовність значень функції (2)
збігається до числа
,
і пишуть![]() .
.

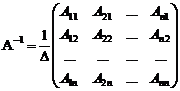 , (1.2)
де
, (1.2)
де 
