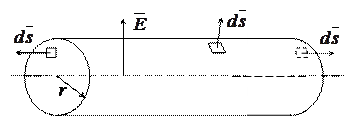19 Билет

1. Поле точечного заряда в однородной среде.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. НАПРЯЖЕННОСТЬ

Факт взаимодействия электрических зарядов на расстоянии можно объяснить наличием вокруг них электрического поля - материального объекта, непрерывного в пространстве и способного действовать на другие заряды.

Поле неподвижных электрических зарядов называют электростатическим.

Характеристикой поля является его напряженность.

Напряженность электрического поля в данной точке - это вектор, модуль которого равен отношению силы, действующей на точечный положительный заряд, к величине этого заряда, а направление совпадает с направлением силы.

Напряженность поля точечного заряда Q на расстоянии r от него равна

2.Передача электромагнитной энергии вдоль проводов линии.

Билет 20

1. Поле заряженной оси и цилиндра.

Под заряженной осью понимают тонкий, теоретически бесконечно длинный металлический проводник.

Под линейной плотностью заряда t понимают заряд, приходящийся на единицу длины оси.

Пусть диэлектрическая проницаемость окружающей среды равна e_a.

Для нахождения напряженности поля в некоторой точке, удаленной на расстояние r от оси, проведем через точку цилиндрическую поверхность так, чтобы ее ось совпала с заряженной осью (рис. 15.6).

 

Рис. 15.6. К определению поля заряженной оси

 

Используем теорему Гаусса, которая применима к замкнутой поверхности (боковая поверхность цилиндра и два его основания). Поток вектора   имеется только через боковую поверхность. Направление   и   на боковой поверхности в каждой точке совпадают, поэтому

или

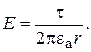 (15.25)

Напряженность в поле заряженной оси изменяется обратно пропорционально расстоянию r точки от оси.

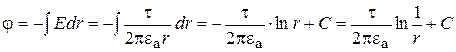 (15.26)

Потенциал изменяется по экспоненциальному закону.

Электрическая емкость определяется как отношение заряда к разности потенциалов между телами. Рассчитаем емкость двух соосных цилиндров (рис. 15.7).

 

Рис. 15.7. Разрез двух соосных цилиндров

 

Напряжение между поверхностями цилиндров

 .

Емкость цилиндрического конденсатора будет равна

 (15.27)

 

2. Излучение электромагнитной волны. Уравнение Даламбера.

3. Будем исходить из уравнения Максвелла  . Домножим обе части на   и учтем, что   и  . получим:

4. .

5. Учтем, что   и  . Тогда получим

6. 

7. 

8. . (28.1)

9. Пользуясь неоднозначностью потенциалов, определяемых с точностью до калибровочного преобразования, для максимального упрощения наложим на них условие:

10.  (28.2)

11. И тогда из (28.1) получим уравнение Даламбера:

12.  (28.3)

13. Условие (28.1) называется условием калибровки Лоренца. Получим теперь уравнение для скалярного потенциала следующим образом:

14.  и учтем, что  . Тогда 

15. .

16. Из (28.2):  . Тогда получим

17.  (28.4)

18. Уравнение (28.4) тоже уравнения Даламбера. Следовательно, для скалярного и векторного потенциалов получили одно и тоже уравнение.

19.  (28.5)

20. Где   - скорость электромагнитных волн в среде. Уравнение (28.5) – уравнение гиперболического типа и описывает волновой процесс, т. е. волны, распространяющиеся в пространстве со скоростью  . В одномерном случае при   решение (28.5) можно представить в виде суммы двух функций:

21. . (28.6)

22. Которое описывает волны, распространяющиеся в двух противоположных направлениях. Функция  представляет собой волну, движущуюся в направлении положительных значений оси Ох со скоростью  , а   - в противоположном направлении.

23. Рассмотрим решение волнового уравнения в сферически симметричном случае, т. е. считая, что в (28.5) F=0, а Ф=Ф(R), где R – расстояние от начала координат до рассматриваемой точки. В этом случае Ф от углов не зависит и оператор Лапласа имеет вид

24. . (28.7)

25. Поэтому волновое уравнение для Ф записывается в виде

26. . (28.8)

27. Решением этого уравнения для  , как и в предыдущем случае, являются произвольные функции от аргумента  и  , т. е. общее выражение для Ф таково:

28. . (28.9)

29. Функция  Представляет волну, движущуюся в радиальном направлении от начала координат со скоростью  . Форма волны при этом не изменяется, а амплитуда уменьшается как 1/R. Эта волна называется расходящейся. Функция   представляет сходящуюся к началу координат волну.

30. Потенциалы поля, а следовательно, и сами поля распространяются в свободном пространстве со скоростью  . В вакууме  ,  , поэтому скорость распространения полей равна скорости света  . Таким образом Электромагнитные волны и всякие изменения электрического и магнитного поля распространяются в вакууме со скоростью света. А это означает, что электромагнитные взаимодействия распространяются со скоростью света. Например, если два точечных заряда покоятся на расстоянии R друг от друга и один из зарядов в некоторый момент сдвинут со своего места, то другой заряд «почувствует» этот сдвиг лишь спустя время  .

Билет 21