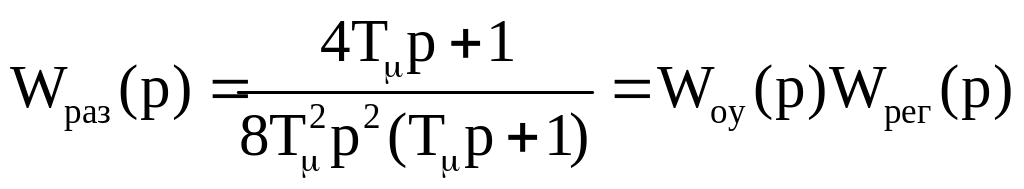Выбор оптимальных параметров настройки типовых регуляторов

Под законом регулирования понимают уравнения связи между управляющим воздействием и величиной ошибки.

Оптимальный закон регулирования можно выбрать исходя из следующих соображений:

Необходимо достичь . Для этого необходимо , что практически не выполнимо, т.к. для этого необходимо, чтобы коэффициент преобразования системы во всем диапазоне частот был постоянным.

Поэтому можно приближенно принять:

и для диапазона частот, где , .

При разложении в ряд Фурье

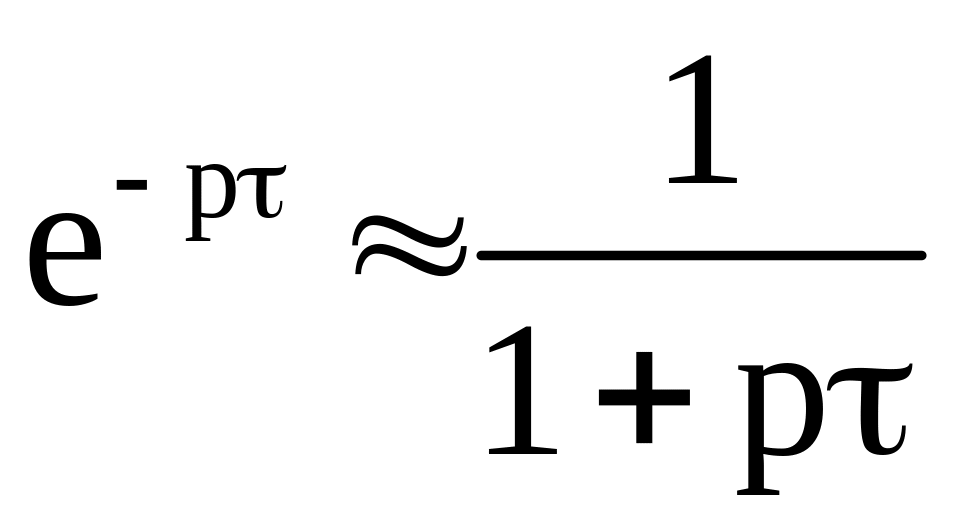
- оптимальная передаточная функция системы в замкнутом состоянии.

Оптимальная передаточная функция системы в разомкнутом состоянии должна быть эквивалентна интегральному звену, что обеспечит всегда монотонный переходный процесс в системе, т.к. в замкнутом состоянии система – апериодическое звено.

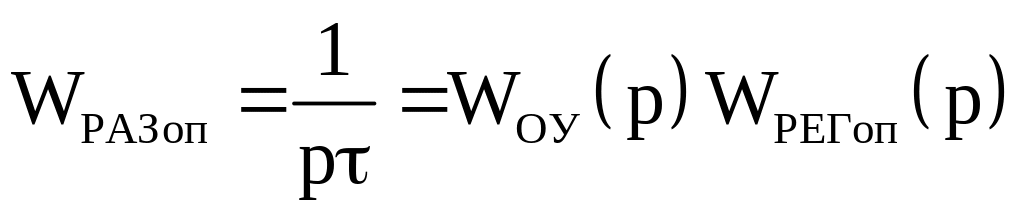
Для линейных законов регулирования параметры настройки можно выбирать с использованием ЛАЧХ.

Для этого строят ЛАЧХ ОУ и желаемую ЛАЧХ; вычитая затем из ЛАЧХ желаемой ЛАЧХ ОУ, определяют структуру и параметры регулятора.

Можно не строить желаемую ЛАЧХ, а, построив ЛАЧХ ОУ и выбранного ориентировочного регулятора, совмещая их, получить желаемую ЛАЧХ выбирая параметры регулятора [метод полной компенсации постоянных времени объекта]

1) Выбор оптимальных параметров настройки регулятора на основании интегральных оценок качества

Можно использовать интегральную оценку (квадратичная простая):

Если на входе

(квадратичная)

– коэффициент, ограничивающий скорость переходного процесса, т.е. величину перерегулирования.

Сложность использования связана с тем, что нужно правильно выбрать .

Для определения оптимальных параметров настройки регулятора нужно найти минимальное значение интеграла.

Квадратичная простая оценка вычисляется по формуле Релея:

– амплитудный спектр сигнала ошибки.

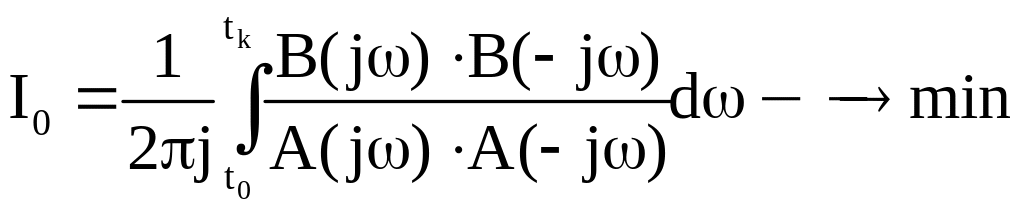
Это интеграл вычислен и существует в таблицах Мак-Ленона, которые позволяют по коэффициентам полиномов и вычислять значения интеграла.

Для определения минимального значения интеграла нужно составить систему уравнений в частных производных по параметрам регулятора и, приравняв их к нулю, решить систему уравнений.

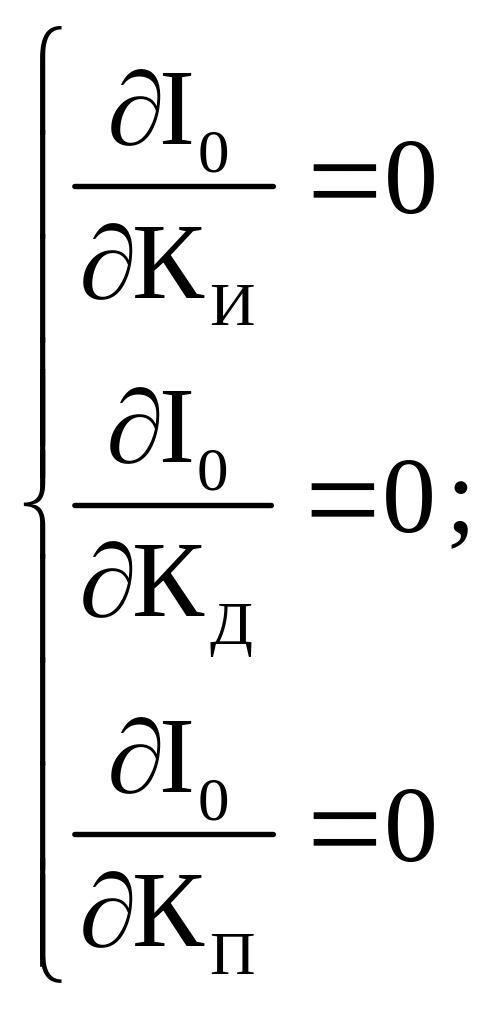
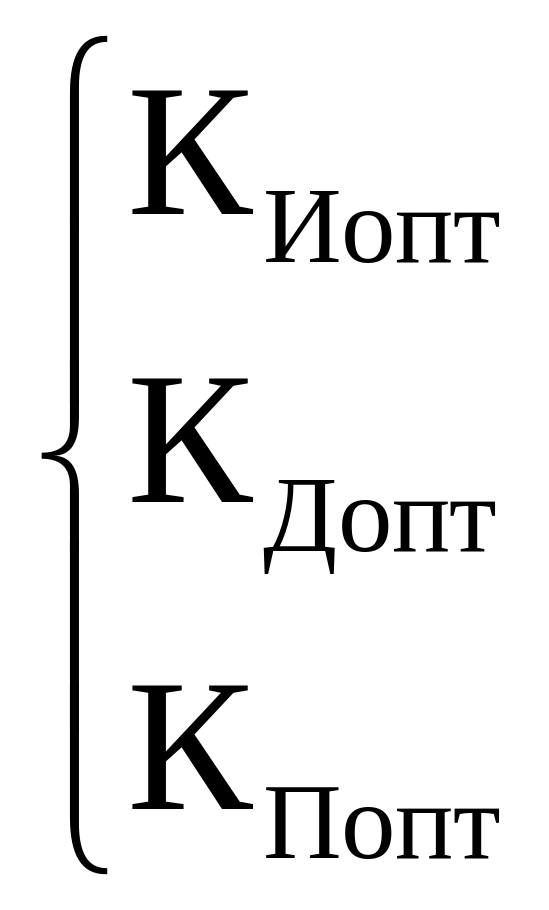
2) Выбор оптимальных параметров настройки регулятора на основании критерия «максимальной степени устойчивости»

Под критерием степенью устойчивости ( ) понимают расстояние ближайшего корня до мнимой оси.

При выборе параметров регулятора на основании критерия задаются степенью устойчивости, которая характеризует:

Если ближайшим к мнимой оси является вещественный корень, а остальные комплексные, но расположены дальше, то переходный процесс с перерегулированием не более 20%.

Характеристическое уравнение запишется т.о., чтобы выделить коэффициенты:

, где

– не содержит параметра регулятора

– содержит параметр регулятора

Это уравнение дифференцируют n раз и составляют систему уравнений, на основании которой и определяют оптимальные параметры настойки регулятора.

3) Настройка регуляторов на модульный и симметричный оптимум

Такую настройку обычно используют для многоконтурных систем управления с подчиненным регулированием, когда один из регуляторов вырабатывает задающие воздействия для второго, стоящего во внутреннем контуре. При этом каждый контур настраивается индивидуально и параметры регулятора определяются оптимизацией каждого контура.

– стабилизирующий регулятор;

– корректирующий регулятор;

, – передаточные функции объекта управления.

При оптимизации структуру регулятора внутреннего контура обычно выбирают из условия минимального времени регулирования и перерегулирования ≤4%.

Такая настройка называется технический (модульный) оптимум.

Этому условию соответствует ЛАЧХ, ФЧХ и системы следующего вида:

Тогда передаточная функция разомкнутого контура:

Модульный оптимум характеризуется тем, что система в замкнутом состоянии эквивалентна колебательному звену:

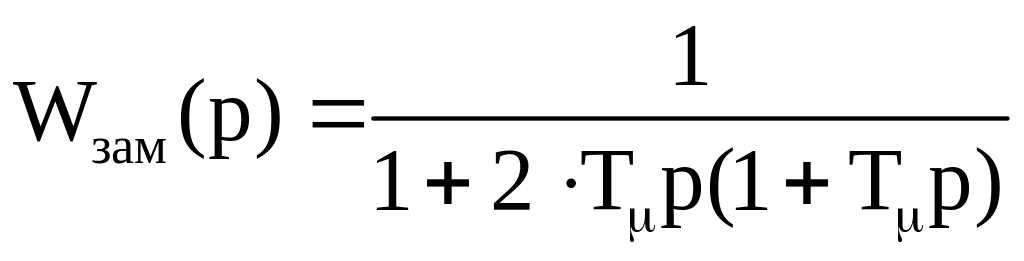
– малая постоянная времени, связанная с временем регулирования, которая должна учитывать все малые постоянные времени настраиваемого контура.

При ступенчатом управляющем воздействии выходная величина в первый раз достигает установившегося значения через время , перерегулирование составляет 4,3%, а запас по фазе 63°.

Настройка регуляторов на симметричный оптимум

При такой настройке ЛАЧХ желаемой системы имеет астатизм 2-го порядка, время первого достижения выходной величиной установившегося значения составляет , максимальное перерегулирование достигает 43%, запас по фазе 37° но при этом в системе переходной процесс с перерегулированием до 40% и выше.