discrete_mathematics

криваючої дужки. Отже, ця послідовність не є пропозиційною формулою. ◄

2. Виписати всі підформули формули:

(((x → y) z) ~ ((¬x) → (y z))).

► Скориставшись процедурою, що описана в попередньому

пункті, дістанемо, що F1, F2, F11, F12, F21, F22, F111, F112, F211, F221,

F222 – це всі підформули даної формули. ◄

Кожна формула A зображує форму або схему складеного висловлення: вона перетворюється на висловлення, якщо замість її пропозиційних змінних підставити якісь конкретні висловлення. Оскільки кожне із підставлених висловлень має значення 0 або 1, то, послідовно обчислюючи значення всіх підформул формули A, одержимо значення формули A на цьому наборі висловлень, яке дорівнюватиме 0 або 1. Підставляючи у формулу A замість її пропозиційних змінних інший набір висловлень, аналогічно обчислимо нове значення формули A і т. д. Оскільки кожне із висловлень набору повністю характеризується своїм значенням (істинно або хибно, тобто 1 або 0), то замість пропозиційних змінних у формулу можна підставляти не самі висловлення, а їхні значення – 1 або 0.

Нехай p1, p2, …, pn – це всі пропозиційні змінні, що входять до формули A; позначатимемо цей факт A(p1, p2, …, pn). Формулі A(p1, p2, …, pn) поставимо у відповідність функцію f(p1, p2, …, pn), що означена на множині впорядкованих наборів (p1, p2, …, pn), де кожне pi набуває значення у множині B = {0, 1}, і значенням функції f є 0 або 1. Значення функції f на наборі значень a1, a2, …, an її змінних p1, p2, …, pn дорівнює значенню формули A(p1, p2, …, pn) при підстановці до неї замість пропозиційних змінних p1, p2, …, pn значень a1, a2, …, an, відповідно. Зауважимо, що кількість елементів в області визначення функції f дорівнює 2n.

Приклад1.6. Обчислити значення формули алгебри висловлень

(((a → (¬ b)) → (b ((¬ c) → a))) ~ (¬ a))

на наборі (1,1,0) значень її змінних, тобто за умови, що a = 1, b = 1, c = 0.

16

► Для цього за допомогою індексів занумеруємо порядок виконання операцій у даній формулі, як було зроблено у прикладі

1.5(1). Матимемо:

(((a →4 (¬1b)) →7 (b 6 ((¬2c) →5 a))) ~8 (¬3a)).

Підставимо замість пропозиційних змінних a, b, c задані вище значення, дістанемо

(((1 →4 (¬11)) →7 (1 6 ((¬20) →5 1))) ~8 (¬31)).

Обчисливши операції 1, 2 та 3, дістанемо вираз

(((1 →4 0) →7 (1 6 (1 →5 0))) ~8 0),

який після обчислення операцій4 та5 набуде вигляду

((0 →7 (1 6 0)) ~ 8 0).

Результатом операції 6 є 0, отже, матимемо ((0 →7 0) ~8 0).

Після виконання операції 7 дістанемо (1 ~ 8 0). Останній вираз має значення 0. Таким чином, значенням даної формули на наборі (1,1,0) буде 0. Аналогічні обчислення можна виконати й для решти семи наборів значень змінних a, b, c. ◄

Функцію f називають функцією істинності для формули A або відповідного складеного висловлення. Для функції істинності f можна побудувати таблицю істинності (табл. 1.3). Традиційно набори значень змінних розташовують у цій таблиці в лексикографічному порядку (див. розд. 2).

Приклад 1.7. Побудувати таблицю істинності для формули із попереднього прикладу.

► У першому рядку кожного стовпця останньої таблиці записано вираз (підформулу) і номер відповідної операції. Наприклад, запис (a→(1)) (4) означає, що результатом операції із номером 4 є імплікація значення пропозиційної змінної a та результату операції з номером 1, а запис ((4)→(6)) (7) означає, що результатом операції з номером 7 є імплікація значення операції із номером 4 і результату операції із номером 6 тощо..

17

◄

18

Формулу алгебри висловлень A(p1, p2, …, pn) називають тав тологією, коли їй відповідає функція істинності, що тотожно до-

Переконатись у тому, що ці формули є тавтологіями, можна за допомогою відповідних таблиць істинності.

Іноді перевірку того, що певна формула є тавтологією, вико-

нують за допомогою способу відшукання контрприкладу (або методу від супротивного). Пояснимо його на прикладах.

Приклад 1.8.

1. Перевірити, чи є тавтологією формула

A = (((a → ¬b) (b → (a c))) (¬ c → ¬ a)) → (a ¬ c).

► Припустимо, що формула A не є тавтологією. Тоді принаймні на одному наборі значень формула A набуває значення 0. Спробуємо відшукати цей набір. Оскільки останньою (головною) операцією формули A є імплікація, то її консеквент має дорівнювати нулю, а антецедент – одиниці. Консеквент (a ¬ c) дорівнює нулю, коли a = 0 та c = 1. Звідси (a → ¬ b) = 1 та (¬ c → ¬ a) = 1. Залишилось з'ясувати, чи може за цих умов вираз (b → (a c)) дорівнювати одиниці. Відповідь позитивна (для b = 0). Отже, ми знайшли набір (0, 0, 1), на якому формула A набуває значення 0, тобто відшукали контрприклад, який свідчить, що формула A не є тавтологією. ◄

2. У разі, коли при спробі відшукати контрприклад для певної формули A отримуємо суперечність, можемо стверджувати, що A – тавтологія.

Наприклад, треба перевірити на тавтологічність формулу

B = (((a → ¬ b) (b → (a c))) (¬ c → ¬a)) → (a ¬ b),

яка є дещо зміненим варіантом попередньої формули A.

► Діючи саме у такий спосіб, матимемо: a = 0 і b = 1, звідки

(a → ¬ b) = 1, (¬ c → ¬ a) = 1, однак (b → (a c)) = 0, що су-

19

перечить припущенню (b → (a c)) = 1. Отже, формула B є тавтологією. ◄

Якщо формула A → B є тавтологією, то кажуть, що формула

A сильніша ніж B, а формула B слабша ніж A.

Формула алгебри висловлень A(p1, p2, …, pn), яка набуває значення 0 на всіх наборах (a1, a2, …, an) значень своїх пропозиційних змінних, називається суперечністю, або тотожно хиб

ною формулою.

Формулу, що не є ні тавтологією, ні суперечністю, називають

нейтральною.

Множину всіх формул алгебри висловлень розбивають на тавтології, суперечності та нейтральні формули.

Формулу, яка не є суперечністю, називають виконуваною,

інакше – невиконуваною.

Приклад 1.9.

1. Показати, що формула алгебри висловлень

(a → (b → ¬ b)) (a → c) (a ¬ c)

є виконуваною.

Для будь-якого набору значень змінних, у якому a = 1 та c = 0, підформула (a ¬ c), а отже, і вся формула набуватиме значення 1, тому ця формула є виконуваною.

2. Довести, що формула A = (a → c) (b → c) алгебри висловлювань є сильнішою за формулу B = (a b) → c.

Для доведення слід відомим способом переконатись, що формула A → B є тавтологією.

3. Визначити, чи є формула алгебри висловлень

((a b) → c) → ((a → c) (b → c))

тавтологією, суперечністю або нейтральною.

За допомогою таблиці істинності або методом відшукання контрприкладу для формули можна переконатись, що ця формула є тавтологією.

4. Чи може суперечність містити тільки операції із множини { , , ~, →}? Відповідь обґрунтувати.

Припустимо, що така формула-суперечність існує. Підставимо замість усіх її пропозиційних змінних значення 1. Усі підформули цієї формули містять тільки операції з множини { , , ~, →}, тому всі вони, отже, і вся формула набуватимуть

20

значення 1 (див. табл. 1.2). Це суперечить нашому припущенню про те, що ця формула є суперечністю. Звідси доходимо висновку, що такої суперечності бути не може.

5. Довести чи спростувати таке твердження: якщо A та B – тавтології, то A B – тавтологія. Чи правильне обернене твердження?

Оскільки A та B – тавтології, то на кожному наборі значень їхніх пропозиційних змінних ці формули набуватимуть значення 1, отже, формула A B також дорівнюватиме 1. Тому наведене твердження є істинним.

Обернене твердження не справджується. Наприклад, якщо A

– тавтологія, а B – суперечність, то A B буде тавтологією, але при цьому не виконуватиметься умова, що A та B – тавтології.

6. Довести чи спростувати таке твердження: якщо A → B – виконувана формула, то A та B – виконувані. Чи правильне обернене твердження?

Це твердження хибне. Наприклад, якщо A – суперечність (тобто не є виконуваною формулою), а B – довільна формула, то A → B буде тавтологією (тобто буде виконуваною формулою).

Обернене твердження справджується. Якщо A та B – виконувані формули, то принаймні на одному наборі значень пропозиційних змінних формула B набуватиме значення 1. Тоді на цьому наборі формула A → B також дорівнюватиме 1, а отже, буде виконуваною.

7. Довести твердження: якщо A та A → B – тавтології, то B – тавтологія (правило висновку, або modus ponens (МР)).

Припустимо, що формула B не є тавтологією. Тоді на якомусь наборі значень пропозиційних змінних формула B набуватиме значення 0. На цьому самому наборі формула A набуватиме значення 1, а формула A → B дорівнюватиме 0, а це суперечить припущенню, що A → B – тавтологія. Отже, припустивши, що формула B не є тавтологією, ми дійшли суперечності, тому справджується, що B – тавтологія.

8.Відомо, що формула A → B є тавтологією, а формула A ~ B

–нейтральна. Що можна сказати про формулу B → A?

Із умов задачі випливає, що існує такий набір значень пропозиційних змінних, на якому формула B набуватиме значення 1, а формула A – значення 0 (на цьому наборі формула A ~ B дорів-

21

нюватиме 0, а формула A → B – 1), а також існує такий набір, на якому обидві формули A та B набуватимуть однакових значень (на цьому наборі обидві формули A ~ B та A → B дорівнюватимуть 1). Тоді на першому із цих наборів формула B → A дорівнюватиме 0, а на другому вона дорівнюватиме 1. Отже, формула

B→ A – нейтральна.

9.Відомо, що B A → ¬ A. Що можна сказати про формулу A?

Формула A є суперечністю. Якщо припустити, що формула A не є суперечністю, то вона виконувана, тобто принаймні на одному наборі значень пропозиційних змінних формула A набуватиме значення 1. Тоді на цьому наборі формула A → ¬ A дорівнюватиме 0, що суперечить умові задачі. ◄

Порядок виконання операцій у формулі визначається за до-

помогою дужок. Задля зменшення їх кількості випускають зовнішні дужки й запроваджують такий порядок (пріоритет) виконання операцій у разі відсутності дужок: ¬, , , →, ~ (за спаданням). Часто у формулах алгебри висловлень випускають знак кон'юнкції і замість a b записують ab.

Для визначення порядку виконання операцій у формулі пріоритету операцій не достатньо. Потрібно ще вказувати для однакових операцій, групуються вони зліва направо чи справа наліво. Наприклад, операції та групуються зліва направо, а операція → – справа наліво. Тому для формули a b c дужки розставляємо таким чином: ((a b) c), для формули a → b → a дужки розставляємо так: (a → (b → a)). Зазначимо, що для операцій та порядок групування не є суттєвим, але для операції → він є важливим. Тому для формули a → b → a при групуванні дужок справа наліво отримаємо формулу (a → (b → a)), яка не еквівалентна попередній формулі (a → (b → a)). Переконайтесь у цьому самостійно. Для операції еквівалентності групування не використовують.

Приклад 1.10. Розставитидужки у формулі: a → b → ¬ b a → c a ¬ c.

► Починаємо із пошуку операцій найвищого пріоритету й беремо відповідну підформулу в дужки. Тут операцією з найви-

22

щим пріоритетом є заперечення. Воно зустрічається двічі. Отримуємо формулу

a → b → (¬ b) a → c a (¬ c).

Наступна за пріоритетом операція – це . Така операція має два аргументи. Беремо відповідні підформули в дужки:

a → b → ((¬b) a) → c (a (¬ c)).

Далі виокремлюємо підформулу з операцією . Дістали a → b → ((¬b) a) → (c (a (¬ c))).

Наступна за пріоритетом операція – імплікація →. Однак тут треба врахувати порядок групування, тому отримуємо остаточний результат:

(a → (b → (((¬ b) a) → (c (a (¬ c)))))). ◄

Структура формули. Розстановка дужок у формулі вказує не лише на порядок виконання операцій, а фактично задає її структуру. Тут важливими є поняття головної операції у формулі та її аргументів.

Приклад 1.11. Проаналізувати структуру формули

(a → (b → (((¬ b) a) → (c (a (¬ c))))))

із прикладу 1.10.

► Головною буде перша імплікація (позначаємо головну операцію зірочкою *). Маємо такий запис:

( a →* (b → (((¬b) a) → (c (a (¬ c)))))).

Далі аналізуємо підформули. Підформули

a та (b → (((¬ b) a) → (c (a (¬ c)))))

задають перший і другий аргументи цієї операції. Для другої підформули головною буде перша імплікація, тобто

(b →* (((¬ b) a) → (c (a (¬ c))))).

Далі, у підформулі

(((¬ b) a) → (c (a (¬ c))))

головною є імплікація, тому отримуємо

(((¬b) a) →* (c (a (¬c)))).

Аргументами є підформули

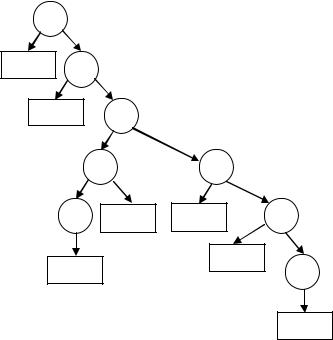
Продовжуючи таким чином, підійдемо до найпростіших підформул a , b, c.

Структуру формули часто подають деревом синтаксичного аналізу формули. У ньому дужки не вказують. Для проаналізованої формули дерево синтаксичного аналізу має вигляд:

c

Наведене дерево дає наочне уявлення про порядок виконання операцій, оскільки спочатку виконуються операції, записані внизу дерева, а потім ті, які йдуть вище. ◄

Проблема розв'язності в алгебрі висловлень – це задача знаходження алгоритму, за допомогою якого для будь-якої формули A алгебри висловлень можна визначити, є A тотожно істинною (тавтологією), чи ні.

Для алгебри висловлень цю проблему можна, зокрема, роз- в'язати такими двома способами:

1) побудувати таблицю істинності для формули A й перевірити, чи складається стовпчик значень A лише з одиниць;

24

2) застосувати спосіб відшукання контрприкладу. Аналогічно можна сформулювати й розв'язати проблему роз-

в'язності для визначення того, чи є певна формула алгебри висловлень суперечністю або виконуваною.

Завдання для самостійної роботи

1. Визначити, чи є наведена послідовність символів формулою алгебри висловлень:

(а) (((x → y) (¬z)) ~ ((¬x) → (y → x)));

(б) (((¬x) ~ ((¬y) + 1)) → (x 5y)); (в) (((¬y) ~ (x (¬z))) → ((¬ y) x)); (г) (((((x → y) ~ (¬z)) x) (¬ y))).

2.Виписати всі підформули даної формули: (а) (((x → (¬ y)) (¬z)) ~ ((¬ x) → (x z)));

(б) ((((y (¬ z)) → (y z)) ~ ((¬ y) x)); (в) ((z → (¬ y)) ((¬x) (¬(y (¬ x)))));

(г) (((¬x y) (x ~ ((¬y) → x)).

3.Занумерувати послідовність виконання операцій у формулі:

(а) (((y ~ (¬ z)) (¬ x)) → ((¬ z) ~ (x y)));

(б) (((x → (¬ y)) → (y ((¬ z) → x))) ~ (¬ x)).

4.Занумерувати послідовність виконання операцій у формулі

зурахуванням їхніх пріоритетів:

(а) (a → ¬ b) (¬ a ~ c) b (c → ¬ (a ~ b));

(б) (a → ¬ ((b c) ¬ a)) → (¬ c b) a ~ ¬ (a → ¬ b).

5. Знайти значення істинності формули:

(а) (a ~ b) ((¬ c → b) (¬ a c) (a ¬ b)) при a = 0, b = 1, c = 0;

(б) ((b → a) (¬ c (a ~ ¬ b))) → (a (d ¬ b)) при a = 1, b = 1, c = 0, d = 1;

(в) ¬ a (a ~ c) (¬ b (¬ c → a)) при a = 1, b = 0, c = 1.

6. Знайти значення істинності складеного висловлення:

(а) Якщо ми успішно складемо іспити (a), то поїдемо відпочивати до моря (b), і ми або успішно складемо іспити, або здійснимо турпохід у Карпати (c) тоді й тільки тоді, коли погода

25