discrete_mathematics

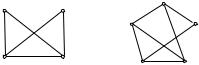
Один із них – задати кожну із множин V та E за допомогою переліку їхніх елементів.

Приклад 4.1. G1 = (V1, E1), де V1 = {v1, v2, v3, v4} і E1 = {(v1, v3),

(v1, v4), (v2, v3), (v2, v4), (v3, v4)} − граф із чотирма вершинами й п'ятьма ребрами, а G2 = (V2, E2), де

V2 = {v1, v2, v3, v4, v5} і

E2 = {(v1, v2), (v2, v4), (v1, v5), (v3, v2), (v3, v5), (v4, v1), (v5, v4)} −

граф із п'ятьма вершинами й сімома ребрами. ◄

Граф G = (V, E) зручно зображати за допомогою рисунка на площині, який називають діаграмою графа G. Вершинам графа G ставлять у бієктивну відповідність точки площини. Точки, що відповідають вершинам v i w, з'єднують лінією (відрізком або кривою) тоді й тільки тоді, коли v i w – суміжні вершини. Зрозуміло, що діаграма графа змінює вигляд залежно від вибору відповідних точок на площині.

Приклад 4.2. На рис. 4.1 подано діаграми графів G1 i G2 із по-

Графи можна задавати також за допомогою матриць. Занумеруємо всі вершини графа G натуральними числами від

1 до n. Матрицею суміжності A графа G називають квадратну n n-матрицю, у якій елемент aij i-го рядка та j-го стовпця дорівнює 1, якщо вершини vi та vj з номерами i та j суміжні, і дорівнює 0 в іншому випадку.

Приклад 4.3. Для графів G1 i G2 маємо відповідно

Очевидно, що матриці суміжності графів симетричні. Занумеруємо всі вершини графа G числами від 1 до n, а всі

його ребра − числами від 1 до m. Матрицею інцидентності B

162

Важливі класи становлять підграфи, які можна отримати в результаті застосування до заданого графа операцій вилучення вершини або вилучення ребра.

Операція вилучення вершини v із графа G = (V, E) полягає у вилученні з множини V елемента v, а з множини E − усіх ребер, інцидентних v.

Операція вилучення ребра e з графа G = (V, E) − це вилучення елемента e змножини E. Прицьому всі вершинизберігаються.

Графи G1 = (V1, E1) і G2 = (V2, E2) називають ізоморфними, якщо існує таке взаємно однозначне відображення ϕ множини

вершин V1 на множину вершин V2, що ребро (v, w) E1 тоді й тільки тоді, коли ребро (ϕ(v), ϕ(w)) E2.

Відображення ϕ називають ізоморфним відображенням, або

ізоморфізмом, графа G1 на граф G2.

Таким чином, ізоморфні графи відрізняються лише ідентифікаторами (іменами) своїх вершин. Із погляду теорії графів ця відмінність неістотна, тому зазвичай ізоморфні графи ототожнюють і, зображаючи графи у вигляді діаграм, або зовсім не ідентифікують їхні вершини, або нумерують вершини натуральними числами.

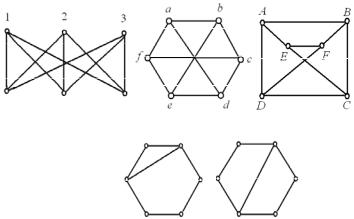
Приклад 4.6. Неважко переконатися, що всі графи на рис. 4.2, ізоморфні між собою, а графи на рис. 4.3 − не ізоморфні.

H1 H2 Рис. 4.3 ◄

165

Наприклад, відображення ϕ множини вершин

V1 = {1,2,3,4,5,6}

графа G1 на множину вершин

V2 = {a, b, c, d, e, f}

графа G2, за яким ϕ(1) = a, ϕ(2) = c, ϕ(3) = e, ϕ(4) = f, ϕ(5) = d, ϕ(6) = b, є ізоморфізмом графа G1 на граф G2. Аналогічно можна побудувати ізоморфне відображення графа G2 на граф G3.

Відношення ізоморфізму є відношенням еквівалентності на сукупності графів.

Граф G = (V, E) називають повним, якщо будь-які дві його вершини суміжні (тобто E = V (2)). Повний граф із n вершинами позначають Kn.

Приклад 4.7.

1. Скільки ребер містить повний граф із n вершинами? Оскільки в повному графі будь-які дві його вершини з'єднані

ребром, то кількість його ребер становить C(n, 2) = n(n – 1)/2. 2. Чи існує повний граф, у якого кількість ребер дорівнює: (а) 15; (б) 18; (в) 199…900…0 (k дев'яток і k нулів)?

(а) Кількість ребер повного графа з n вершинами дорівнює n(n – 1)/2. Рівняння n(n – 1)/2 = 15 має корені 6 і –5. Отже, існує повний граф із6 вершинами, кількість реберу якому дорівнює 15.

(б) Рівняння n(n – 1)/2 = 18 не має натуральних коренів, тому такий повний граф не існує.

(в) Розглянемо рівняння

n(n – 1) = 2 199…900…0 = 200…0 199…9 (k нулів і k дев'яток).

Число у правій частині цього рівняння можна подати у вигляді 2 10k(2 10k – 1), тобто n = 2 10k. Отже, такий повний граф існує й має 2 10k вершин. ◄

Для графів можна означити операції об'єднання, перетину й доповнення.

Об'єднанням графів G1 = (V1, E1) і G2 = (V2, E2) називають

граф G = (V1 V2, E1 E2); позначають G = G1 G2. Об'єднання G = G1 G2 називають прямою сумою графів G1 i

G2, якщо V1 ∩ V2 = .

Перетином і різницею графів G1 = (V, E1) i G2 = (V, E2) з од-

наковими множинами вершин називають відповідно графи

G′= (V, E1 ∩ E2) i G′′ = (V, E1 \ E2); позначають G′= G1 ∩ G2 і G′′ = G1 \ G2.

166

Доповненням графа G = (V, E) називають граф

G = (V, V (2) \ E).

Отже, граф G має ту саму множину вершин V, що й граф G, а вершини графа G суміжні тоді й лише тоді, коли вони несуміжні в G. Для графа G із n вершинами виконується G = Kn \ G.

Графи G1 i G2 ізоморфні тоді й тільки тоді, коли ізоморфні їхні доповнення G1 i G2 .

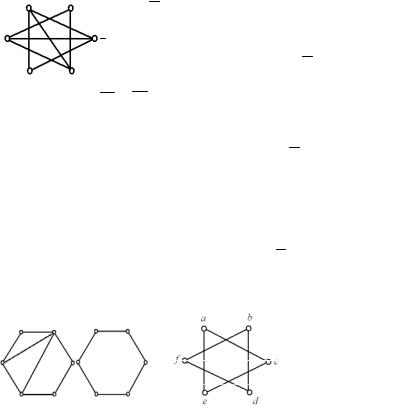
Приклад 4.8. Об'єднання й перетин графів H1 і H2 із прикладу 4.6 подано на рис. 4.4, а доповнення графів G2 i H2 – на рис. 4.5.

Граф G, ізоморфний своєму доповненню G, називають са

модоповнювальним.

Приклад 4.9.

1. Граф G = (V, E), у якому

V = {a, b, c, d} і E = {(a, b), (b, c), (c, d)},

самодоповнювальний.

2. Чому дорівнює кількість ребер у графі G, якщо граф G має

n вершин і k ребер?

n(n – 1)/2 – k (див. приклад 4.7(1)).

3.Визначити, скільки існує попарно неізоморфних графів, які мають 8 вершин і 25 ребер.

Доповнення кожного з таких графів матиме 8 вершин і 3 ребра (див. попередній пункт). Існує тільки 5 попарно неізоморфних графів з такими параметрами. Доповнення кожного із цих п'яти графів задовольняють умову задачі.

4.Довести, що кількість вершин будь-якого само доповню-

вального графа дорівнює або 4k, або 4k + 1, k N.

167

Якщо m – кількість ребер самодоповнювального графа G = (V, E) з n вершинами, то n(n – 1)/2 – m = m, тобто

n(n – 1) = 4m.

Із того, що число n(n – 1) кратне 4, випливає, що n = 4k або n = 4k + 1, k N. ◄

Завдання для самостійної роботи

1. Накресліть діаграму повного графа з n вершинами Kn для: (а) n = 2; (б) n = 3; (в) n = 4; (г) n = 5.

2. Чи існує повний граф, у якого кількість ребер дорівнює: (а) 21; (б) 27; (в) 500…0500…0 (у кожній групі k нулів); (г) 8k 2 + 2k, k N?

3.Довести, що для довільного графа G об'єднання G G є повним графом.

4.Нехай графи G1 = (V, E1) i G2 = (V, E2) задано за допомогою матриць суміжності A1 та A2, відповідно (|V | = n). Визначити матрицю суміжності A для графа:

5. Довести, що ізоморфне відображення ϕ графа G1 = (V1, E1) на граф G2 = (V2, E2) установлює певне взаємно однозначне відображення ψ множини ребер E1 на множину ребер E2.

6.Довести, що ізоморфні графи мають однакову кількість вершин та однакову кількість ребер.

7.Довести, що графи ізоморфні тоді й тільки тоді, коли ізоморфні їхні доповнення.

8.Визначити, скільки існує попарно неізоморфних графів, які мають:

(а) 8 вершин і 26 ребер; (б) 5 вершин і 78 ребер; (в) 6 вершин і 12 ребер.

9.Знайти нетривіальний самодоповнювальний граф із найменшою кількістю вершин.

10.Довести, що довільний самодоповнювальний граф містить або 4k 2 − k, або 4k 2 + k ребер, k N.

168

4.3. Графи та бінарні відношення

Між множиною всіх графів із множиною вершин V і множиною всіх антирефлексивних симетричних бінарних відношень на V існує взаємно однозначна відповідність: графу G = (V, E) відповідає таке відношення R на V, що (v, w) R тоді й тільки тоді, коли (v, w) E, v, w V. Зокрема, порожньому графу G = (V, ) відповідає порожнє відношення на V (R = ), а повному графу − відношення (V V) \ iV, де iV – діагональне (тотожне) відношення: iV = {(v, v) | v V }.

Очевидно, що операціям об'єднання, перетину й доповнення графів відповідають аналогічні операції для відношень. Якщо графам G1 i G2 відповідають відношення R1 i R2, то гра-

фам G1 G2, G1 ∩ G2 і G1 – відношення R1 R2, R1 ∩ R2 i

R1 \ iV = (V V) \ (R1 iV).

Якщо R – транзитивне відношення, то у відповідному графі G для кожної пари ребер (v, w), (w, u) E існує замикальне ребро

(v, u) E.

4.4. Степені вершин графа

Степенем δ(v) вершини v називають кількість інцидентних їй ребер. Вершину степеня 0 називають ізольованою, а вершину степеня 1 − кінцевою (або висячою).

Кубічним називають граф, степені всіх вершин якого дорівнюють 3.

У будь-якому графі G = (V, E) виконується рівність

Справедливість цього твердження випливає з того, що кожне ребро графа інцидентне двом вершинам, тому воно вносить у суму степенів усіх вершин рівно дві одиниці.

Приклад 4.10.

1. Як визначити степінь певної вершини графа G за його матрицею суміжності A?

169

Степінь вершини v із номером i дорівнює сумі елементів i-го рядка матриці A, оскільки ця сума визначає кількість вершин, суміжних із вершиною v.

2. Нехай A − матриця суміжності графа G із n вершинами. Довести, що i-й діагональний елемент матриці A2 дорівнює степеню δ(vi) i-ї вершини графа G, i = 1, 2, …, n.

Елемент аіі(2) матриці A2

аіі(2) = ∑aik aki = ∑aik2 = ∑aik , k k k

оскільки aik = aki і aij{0, 1}.

Отже, аіі(2) = δ(vi) (див. попередню задачу).

3. Довести, що в будь-якому графі з n вершинами (n ≥ 2) завжди знайдуться принаймні дві вершини з однаковими степенями.

Припустимо, що існує граф G із n вершинами, усі степені вершин якого попарно різні. Ці степені можуть дорівнювати 0, 1, 2, ..., n – 1. Однак якщо в графі G є вершина степеня 0 (ізольована), то в ньому не може бути вершини степеня n – 1. Отже, степені принаймні двох вершин збігаються.

4. Визначити, чи існує граф із шістьма вершинами, степені

(а) Такий граф не існує, тому що сума степенів усіх його вершин непарна, що суперечить рівності (4.1).

(б) Такий граф існує, його матриця суміжності

(в) Граф із такими степенями вершин не існує. За умовою він має дві ізольовані вершини, отже, максимальне значення степеня для будь-якої з решти чотирьох вершин – 3, тобто в такому графі не може бути вершини зі степенем 4.

5. Довести, що доповнення жодного кубічного графа не є кубічним графом.

170

Припустимо, що такий кубічний граф G із n вершинами існує. Тоді із того, що степені всіх вершин графа G і його доповнення дорівнюють 3, випливає, що (n – 1) – 3 = 3, тобто n = 7. Звідси

∑ іδ(vі ) = 2 7 = 21,

що суперечить рівності (4.1). ◄

Завдання для самостійної роботи

1.Чому дорівнює степінь кожної вершини у повному графі з n вершинами?

2.Як визначити степінь певної вершини графа G за його матрицею інцидентності B?

3.Скільки вершин має бути в кубічному графі? Скільки ребер

утакому графі?

4.У графі з n вершинами тільки дві вершини мають однакові степені. Чи можуть обидві ці вершини мати степінь 0 або степінь n – 1?

5.У футбольному турнірі беруть участь 15 команд. Довести, що в будь-який момент знайдеться команда, яка зіграла парну кількість матчів.

6.Довести, що в ізоморфних графів кількість вершин степеня k однакова для довільного k.

7.Визначити, чи існує граф із шістьма вершинами, степені яких дорівнюють:

4.5. Шлях у графі. Зв'язність графів

Маршрутом (або шляхом) у графі G = (V, E) називають послідовність

вершин vi і ребер ei таку, що кожні два сусідні ребра в ній мають спільну вершину, отже, ei = (vi, vi + 1), i = 1, 2, …, k. Вершину v1 називають початком, а вершину vk + 1 − кінцем шляху. Усі інші вершини цього шляху називають проміжними, або внутрішніми.

171