
- •111Equation Chapter 1 Section 1основная часть
- •1 Обзор литературы
- •1.1 Основы теории движения исз
- •1.1.1 Уравнения движения
- •1.1.2 Уравнения движения центра масс исз
- •1.2 Моделирование возмущающих сил, действующих на исз
- •1.2.1 Возмущения, связанные с Землей
- •1.2.2 Возмущения от Луны и Солнца
- •1.2.3 Возмущения от светового давления
- •1.2.4 Возмущения от сопротивления атмосферы
- •1.2.5 Эффект Пойнтинга-Робертсона
- •1.3 Солнечно-синхронные орбиты
- •1.4 Определение местоположения резонансных областей
- •1.4.1 Критические аргументы и их частоты
- •2 Постановка задачи работы
- •3 Способы и методы решения задачи
- •3.1 Описание программного комплекса «Численная модель движения искусственных спутников Земли»
- •3.2 Численное моделирование движения солнечно-синхронных спутников
- •4 Результаты и их обсуждение
111Equation Chapter 1 Section 1основная часть
1 Обзор литературы
1.1 Основы теории движения исз
1.1.1 Уравнения движения
В теории движения искусственных спутников Земли используют уравнения небесной механики, в которых учитываются возмущения, которые характерны для движения искусственных спутников Земли: несферичность гравитационного поля Земли, притяжение Луны и Солнца, световое давление, сопротивление атмосферы и другие.
Уравнения
Ньютона-Эйлера для большой полуоси а,
эксцентриситета е,
момента прохождения перицентра
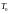 ,
наклона i,
долготы восходящего узла ,
аргумента перицентра
имеют вид [1]:
,
наклона i,
долготы восходящего узла ,
аргумента перицентра
имеют вид [1]:
 212\* MERGEFORMAT (.)
212\* MERGEFORMAT (.)
где
 гравитационный
параметр, м3/c;
гравитационный
параметр, м3/c;
G – гравитационная постоянная, м3кг1с2;
M – масса возмущающего тела, кг;
 истинная
аномалия, рад;
истинная
аномалия, рад;
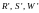 компоненты возмущающего ускорения,
направленные вдоль радиуса-вектора, по
касательной к траектории в направлении
движения и по нормали, соответственно.
компоненты возмущающего ускорения,
направленные вдоль радиуса-вектора, по
касательной к траектории в направлении
движения и по нормали, соответственно.
В том случае, если все возмущающие силы обладают потенциалом, удобно использовать уравнения движения Лагранжа:
 313\* MERGEFORMAT (.)
313\* MERGEFORMAT (.)
1.1.2 Уравнения движения центра масс исз
Уравнения движения центра масс ИСЗ в прямоугольной инерциальной системе координат, связанной с центром Земли, имеют вид [1]:
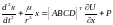 414\* MERGEFORMAT (.)
414\* MERGEFORMAT (.)
Здесь
 вектор положения
объекта, t
физическое время,
вектор положения
объекта, t
физическое время,
 гравитационный
параметр центрального тела; r
– модуль вектора положения. Возмущающее
ускорение, стоящее в правой части
уравнений движения, разделено на два
слагаемых. Первое содержит все возмущающие
ускорения, производимые силами, имеющими
потенциал, к которым в рассматриваемом
случае относятся все возмущения,
связанные с Землей. Поскольку все эти
силы вычисляются в системе координат,
жестко связанной с Землей, а уравнения
движения интегрируются в инерциальной
системе координат, перед первым слагаемым
стоит произведение матриц
гравитационный
параметр центрального тела; r
– модуль вектора положения. Возмущающее
ускорение, стоящее в правой части
уравнений движения, разделено на два
слагаемых. Первое содержит все возмущающие
ускорения, производимые силами, имеющими
потенциал, к которым в рассматриваемом
случае относятся все возмущения,
связанные с Землей. Поскольку все эти
силы вычисляются в системе координат,
жестко связанной с Землей, а уравнения
движения интегрируются в инерциальной
системе координат, перед первым слагаемым
стоит произведение матриц
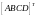 для преобразования координат из земной
вращающейся системы в земную инерциальную.
Причем матрица А задает движения
полюса, D
матрица прецессии, C
– матрица нутации, B
– матрица, осуществляющая преобразование
инерциальной системы истинной даты во
вращающуюся систему истинной даты. Ко
второму слагаемому относятся все
возмущающие ускорения, обусловленные
силами, не связанными с гравитационным
потенциалом Земли. В данном случае это
возмущающее влияние Луны и Солнца,
световое давление, сопротивление
атмосферы. Кроме того, при высокоточном
прогнозировании движения ИСЗ в уравнения
движения должны быть введены релятивистские
поправки, связанные с отклонением
метрики реального физического пространства
от ньютоновской метрики уравнений.
для преобразования координат из земной
вращающейся системы в земную инерциальную.
Причем матрица А задает движения
полюса, D
матрица прецессии, C
– матрица нутации, B
– матрица, осуществляющая преобразование
инерциальной системы истинной даты во
вращающуюся систему истинной даты. Ко
второму слагаемому относятся все
возмущающие ускорения, обусловленные
силами, не связанными с гравитационным
потенциалом Земли. В данном случае это
возмущающее влияние Луны и Солнца,
световое давление, сопротивление
атмосферы. Кроме того, при высокоточном
прогнозировании движения ИСЗ в уравнения
движения должны быть введены релятивистские
поправки, связанные с отклонением
метрики реального физического пространства
от ньютоновской метрики уравнений.
1.2 Моделирование возмущающих сил, действующих на исз
1.2.1 Возмущения, связанные с Землей
Представление потенциала Земли в виде разложения по сферическим функциям в системе координат, жестко связанной с Землей, имеет вид [2]:
 515\* MERGEFORMAT (.)
515\* MERGEFORMAT (.)
Потенциал Земли использовался в форме представления:
 616\* MERGEFORMAT (.)
616\* MERGEFORMAT (.)
где
 средний
экваториальный радиус Земли, а шаровые
функции
средний
экваториальный радиус Земли, а шаровые
функции
 717\* MERGEFORMAT (.)
717\* MERGEFORMAT (.)
и их производные вычислялись с помощью рекуррентного алгоритма Киннингема.
В задачах высокоточного моделирования
движения искусственных спутников земли
Международная служба вращения Земли
(IERS) рекомендует использовать,
как стандартную, модель геопотенциала
EGM96, имеющую 360-й порядок
и степень. В качестве масштабирующих
параметров с коэффициентами данного
разложения геопотенцила нужно использовать
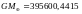 кг3/с2
произведение
гравитационной постоянной на массу
Земли и
кг3/с2
произведение
гравитационной постоянной на массу
Земли и
 м
экваториальный
радиус Земли.
м
экваториальный
радиус Земли.
Выбор коэффициентов
 и
и
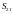 реализуется следующим образом. Полное
определение мгновенных значений этих
двух коэффициентов с учетом полюсного
прилива неупругой Земли дается как
реализуется следующим образом. Полное
определение мгновенных значений этих
двух коэффициентов с учетом полюсного
прилива неупругой Земли дается как
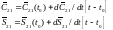 818\* MERGEFORMAT (.)
818\* MERGEFORMAT (.)
где
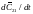 и
и
 производные по
времени, определенные на эпоху
производные по
времени, определенные на эпоху
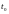 = 1 января 2000 г. есть
= 1 января 2000 г. есть
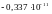 год1
и
год1
и
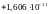 год1
соответственно, нормированные
коэффициенты
год1
соответственно, нормированные
коэффициенты
 на 1 января 2000 г. задаются как
на 1 января 2000 г. задаются как
 919\* MERGEFORMAT (.)
919\* MERGEFORMAT (.)
Вычисление поправок от приливов к
коэффициентам геопотенциала выполняется
двухшаговым способом. На первом шаге
оценивается часть приливного потенциала,
связанная с номинальными значениями
чисел Лява
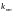 :
:
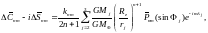 10110\* MERGEFORMAT (.)
10110\* MERGEFORMAT (.)
где
номинальное число
Лява степени n и порядка
m;
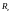 экваториальный
радиус Земли;
экваториальный
радиус Земли;
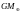 гравитационный
параметр Земли,
гравитационный
параметр Земли,
 гравитационный
параметр Луны (j = 2) и
Солнца (j = 3);
гравитационный
параметр Луны (j = 2) и
Солнца (j = 3);
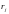 геоцентрическое
расстояние до Луны или Солнца;
геоцентрическое
расстояние до Луны или Солнца;
 фиксированная
западная долгота (от Гринвича) Луны или
Солнца;
фиксированная
западная долгота (от Гринвича) Луны или
Солнца;
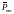 нормированная
присоединенная функция Лежандра,
связанная с классической (ненормированной)
функцией соотношением
нормированная
присоединенная функция Лежандра,
связанная с классической (ненормированной)
функцией соотношением
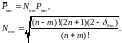 11111\* MERGEFORMAT (.)
11111\* MERGEFORMAT (.)
Соответственно нормированные коэффициенты
геопотенциала
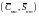 связаны с ненормированными коэффициентами
связаны с ненормированными коэффициентами
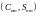 как
как
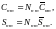 12112\* MERGEFORMAT (.)
12112\* MERGEFORMAT (.)
В результате из уравнения 110 имеем
поправки
 и
и
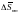 для n = 2 и 3 и всех m
независимо от поправок для частотной
зависимости, оцениваемых на втором
шаге.
для n = 2 и 3 и всех m
независимо от поправок для частотной
зависимости, оцениваемых на втором
шаге.
Далее на первом шаге вносятся поправки в коэффициенты четвертой степени, производимые приливами второй степени:
 13113\* MERGEFORMAT (.)
13113\* MERGEFORMAT (.)
причем m = 0, 1, 2.
На шаге 2 в вычисленные на первом шаге
величины вносятся частотно зависимые
поправки. Вклад в
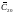 от долго периодических приливных
компонент различной частоты f
есть
от долго периодических приливных
компонент различной частоты f
есть
 14114\* MERGEFORMAT (.)
14114\* MERGEFORMAT (.)
Вклад в
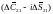 от суточных приливных компонент и в
от суточных приливных компонент и в
 от полусуточных компонент задается
формулой
от полусуточных компонент задается
формулой
 15115\* MERGEFORMAT (.)
15115\* MERGEFORMAT (.)
Здесь
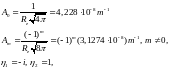 16116\* MERGEFORMAT (.)
16116\* MERGEFORMAT (.)
 разность между
разность между
 ,
определённой как
,
определённой как
 на частоте f, и
номинальной величиной
на частоте f, и
номинальной величиной
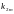 в смысле
в смысле
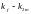 плюс вклад океанических приливов;
плюс вклад океанических приливов;
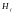 амплитуда (в метрах)
члена с частотой f
в гармоническом разложении потенциала,
производимого приливом;
амплитуда (в метрах)
члена с частотой f
в гармоническом разложении потенциала,
производимого приливом;
 17117\* MERGEFORMAT (.)
17117\* MERGEFORMAT (.)
где
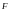 пятимерный вектор
фундаментальных аргументов теории
нутации,
пятимерный вектор
фундаментальных аргументов теории
нутации,
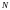 пятимерный вектор
множителей к переменным Делоне для
нутационной частоты
пятимерный вектор
множителей к переменным Делоне для
нутационной частоты
 есть среднее гринвичское звездное
время, выраженное в угловых единицах.
есть среднее гринвичское звездное
время, выраженное в угловых единицах.
