Умножение с младших разрядов в дополнительном коде

Алгоритм:

[Z]_дк= (...(0+[X]_дк*[y_n+1– y_n])*2^-1+ [X]_дк*[y_n– y_n-1])*2^-1+ ...

... + [X]_дк*[y₂– y₁])*2^-1+ [X]_дк*[y₁– y₀]

Если y_n= y_n+
1, то производится сдвиг частичного произведения.

Если y_n= 0 и y_n+1= 1, то к частичному произведению прибавляется [X]_дк

Если y_n= 1 и y_n+1= 0, то из частичного произведения вычитается [X]_дк.

Пример:

Умножение со старших разрядов в дополнительном коде

[Z]_дк= [X]_дк*[Y]_дк= [X]_дк*(y₁– y₀) + [X]_дк*(y₂– y₁)*2^-1+ ... +

+ [X]_дк*(y_n+1– y_n)*2^-n

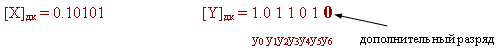
[-X]_дк= 1.01011

[Z]_дк= [-X]_дк+ [X]*2^-1+ [X]_дк*2^-2*0 + [-X]_дк*2^-3+

+ [X]_дк*2^-4+ [-X]_дк*2^-5

₊1.01011 [-X]_дк

0.010101 [X]_дк*2^-1

________

₊1.101011

1.11101011 [-X]_дк*2^-3

__________

₊1.10010111

0.000010101 [X]_дк*2^-4

___________

₊1.101000011

1.1111101011 [-X]_дк*2^-5

____________

1.1001110001

Ответ: [Z]_дк= 1.1001110001

9. Лекция: Деление



Страницы: 1 \| 2\|3\|4\|вопросы\|»	\| учебники\|для печати и PDA\|ZIP

Если Вы заметили ошибку - сообщите нам, или выделите ее и нажмите Ctrl+Enter

В лекции даны методы деления чисел с фиксированной запятой в прямых кодах и дополнительных (обратных) кодах. Описаны операции над числами с плавающей запятой – умножение, деление, сложение, вычитание.



Реализация операции деления в ЭВМ в двоичной системе счисления выполняется проще, чем в десятичной. Это объясняется тем, что при определении каждой цифры частного нужно сделать только одну пробу. Если числа X и Y заданы в прямом коде, и они представлены с фиксированной запятой, то для выполнения деления используются два основных алгоритма: со сдвигом и автоматическим восстановлением остатка; со сдвигом делителя и автоматическим восстановлением остатка. Пусть: [X]_пк= sign X. x₁x₂..x_n [Y]_пк = sign Y. y₁y₂..y_n [Z]_пк = [X]_пк/[Y]_пк = sign Z. z₁z₂..z_n X и Y должны быть такими, чтобы: \|Z\| < 1 (то есть фиксированная запятая) Деление в прямом коде со сдвигом и автоматическим восстановлением остатка sign Z = sign X sign Y \|X\| - \|Y\| = ₀ Если ₀0, то z₀= 1 и 2₀- \|Y\| =₁(z₀– целая часть результата). Если ₀< 0, то z₀= 0 и 2₀+ \|Y\| =₁ и т. д. Пример: [X]_пк= 0.100 [Y]_пк= 1.110 sign Z = 1 0 = 1 [-\|Y\|]_дк= 1.010 ₊0.100 = [\|X\|]_дк 1.010 = [-\|Y\|]_дк 1.110 = ₀= [\|X\|]_дк+ [-\|Y\|]_дк< 0, z₀= 0 ₊1.100 = 2₀(сдвиг в ДК отрицательного числа) 0.110 = [\|Y\|]_дк 0.010 = ₁= 2₀+ [\|Y\|]_дк> 0, z₁= 1 ₊0.100 = 2₁ 1.010 = [-\|Y\|]_дк 1.110 = ₂= 2₁+ [-\|Y\|]_дк< 0, z₂= 0 ₊1.100 = 2₂(сдвиг в ДК отрицательного числа) 0.110 = [\|Y\|]_дк 0.010 = ₃= 2₂+ [\|Y\|]_дк> 0, z₃= 1 Ответ: [Z]_пк= 1.101 Деление в прямом коде со сдвигом делителя и автоматическим восстановлением остатка sign Z = sign X sign Y \|X\| - \|Y\| = ₀ Если ₀0, то z₀= 1. Если₀< 0, то z₀= 0. Разрядная сетка (n + d) разрядов, где d = log₂n Пример: 1) [X]_пк= 1.1001 2) [Y]_пк= 1.1011 n = 4, d = 2 Ответ: [Z]_пк= 0.1100