Функции 4-х переменных
Для функций 4-х переменных применяются диаграммы следующего вида:
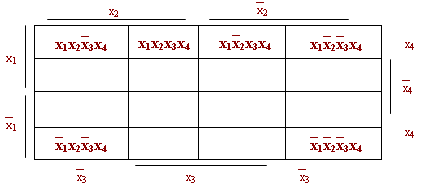
Все, что было сказано относительно функций 2-х, 3-х переменных справедливо и в данном случае. Но данная диаграмма обладает дополнительной особенностью: при поиске минимальной формы функции необходимо считать склееными правый край с левым и верхний с нижним.
Говорят, что для удобства целесообразно считать данную диаграмму написанной на поверхность тора.
Пример:
f(x1,x2,x3,x4)
= x1x2x3x4
x1x2x3x4
x1x2x3x4
x1x2x3x4
x1x2x3x4
x1x2x3x4
Составим диаграмму:
fmin(x1,x2,x3,x4)
= x1x4
x3x4
Заметим, что на основании свойства диаграммы четыре единицы, стоящие в угловых клетках диаграммы соответствуют конституентам, которые склеиваются между собой.
Итак, дадим формализированное описание метода.
Опредение. Правильной конфигурацией ранга К называется совокупность единиц (нулей), образующая прямоугольник площадью 2к.
Для минимизации функции, зависящей от n аргументов, отыскиваются правильные конфигурации вначале n-1 ранга, затем n-2 ранга и т.д.
Далее определяется накрытие найденных правильных конфигураций совместной проекцией соответствующих строк и столбцов, которая выделяет данную правильную конфигурацию.
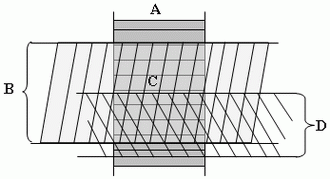Рис.
4.1.Определение правильных
конфигураций
C– правильная конфигурация
A,B,D– проекции конфигурации
А*В– результат склеек
Свойства диаграмм Вейча
С помощью диаграмм Вейча можно находить:
минимальную форму по СКНФ
минимальную форму по ДНФ и КНФ функции
все одинаково минимальные формы
минимальную форму неполностью определенных функций.
Пусть f(x1x2x3) задана не в виде СДНФ, а в ДНФ:
f(x1x2x3)
= x1x2
x1x2x3
x1x2
Заполним соответствующую диаграмму:
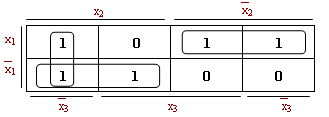
Так как x1x2= x1x2(x3
x3)
= x1x2x3
x1x2x3,
то в соответствующие клетки диаграммы
поставлены единицы.
Поэтому: fmin(x1,x2,x3)
= x2x3
x1x2
x1x2
Преимущество метода: простота и наглядность для небольшого числа аргументов.
Недостатки: неприменяемость метода для большого числа аргументов (> 6) вследствие сложности диаграмм и потери наглядности.
|
5. Лекция: Минимизация неполностью определенных функций | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Страницы: 1 | 2 | 3 | вопросы | » |
| учебники | для печати и PDA | ZIP | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Если Вы заметили ошибку - сообщите нам, или выделите ее и нажмите Ctrl+Enter | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
В лекции представлена минимизация неполностью определенных функций, дан синтез функций в базисах штрих Шеффера и стрелка Пирса, даны подходы к минимизации конъюнктивных форм. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Очень часто, если не в большинстве случаев, работа конкретного устройства описывается с помощью неполностью определенной функции, так как некоторые комбинации входных сигналов не подаются или являются запрещенными. Определение. Неполностью определенной функцией является такая переключательная функция, значения которой на некоторых наборах аргументов могут быть произвольными (т.е. равными "0" или "1").
Определение.
Пусть функция f(x1,x2,...xn)
не определена на "р" наборах
аргументов. Тогда полностью определенную
функцию
Очевидно, существует 2р различных функций, эквивалентных f(x1,x2,...xn).
Задача минимизации
f(x1,x2,...xn)
состоит в выборе такой эквивалентной
Введем две
вспомогательные эквивалентные функции
ТЕОРЕМА.
МДНФ неполностью определенной
f(x1,x2,...xn)
совпадает с дизъюнкцией самых коротких
импликант
Пример: Пусть задана f(x1,x2,...xn) в виде следующей таблицы:
Тогда
а
Найдем простые
импликанты
Простые импликанты
Построим импликантную матрицу.
Выполним
оптимальное покрытие конституент
единицы
f1min(x1x2
x3
x4)
= 11- -
f2min(x1x2
x3
x4)
= 11- -
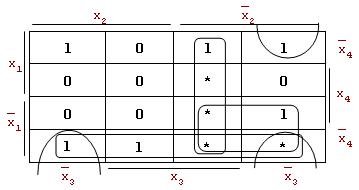
Минимизация с помощью диаграмм Вейча неполностью определенных функций в наглядной и удобной форме позволяет отыскать минимальные формы. Пример: Рассмотрим функцию f(x1x2 x3 x4) и найдем ее минимальную форму. Заполнить диаграмму Вейча по следующим правилам: в клетки диаграммы поставим единицы, которые соответствуют конституентам единицы, нули – для отсутствующих конституент и символ неопределенности – "*" (звездочка) – в остальные.
Видно, что в клетки для конституент: x1x2x3x4, x1x2x3x4, x1x2x3x4 целесообразно "поставить" единицы вместо символов неопределенности, так как в этом случае образуется правильная конфигурация 2-го ранга, которая покрывается произведением x2x3. Аналогично и в клетку x1x2x3x4 нужно "поставить" единицу.
Итак, fmin(x1x2
x3
x4)
= x2x3
Замечание. Все, что было сказано относительно минимизации функции, представленной в СДНФ или ДНФ справедливо для функции, заданной в СКНФ или КНФ. В этом случае необходимо отыскивать правильные конфигурации, образованные нулями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(x1,x2,...xn)
будем считать эквивалентной к
f(x1,x2,...xn),
если ее значения на тех наборах, на
которых f(x1,x2,...xn)
определена, совпадают. 
(x1,x2,...xn),
которая имеет простейшую форму. 
0(x1,x2,...xn),
1(x1,x2,...xn),
которые принимают на запрещенных
наборах аргументов значения 0 и 1
соответственно. 
1(x1,x2,...xn),
которые совместно накрывают все
конституенты единицы
0(x1,x2,...xn),
и ни одна из которых не является лишней.
0(x1x2x3x4)
= 0
5
8
12
15
= x1x2x3x4
x1x2x3x4
x1x2x3x4
x1x2x3x4
x1x2x3x4
= 0000
0101
1000
1100
1111,
1(x1x2x3x4)
= 0
1
2
3
5
8
10
12
13
14
15
= 0000
0001
0010
0011
0101
1000
1010
1100
1101
1110
1111
1(x1x2x3x4)
1
1(x1x2x3x4)
1(x1x2x3x4)
= 0-01
-101
110-
11-0
00-
-
-0-0
1-
-0
11-
-
0
1
0
простыми импликантами
1
и получаем минимальную форму функции
f(x1x2
x3
x4)
-0-0
-101
= x1x2
x2x4
x2x3x4
-0-0
0-01
= x1x2
x2x4
x1x3x4
x1x4
x3x4
x1x2.