Электродинамика

I. Основные понятия и принципы электродинамики.

Электрический заряд и эм поле.

Электрический заряд – физическое понятие отражающее свойство заряженных тел:

1. Создавать ЭМ поле

2. Испытывать на себе действие ЭМ поля

Свойства заряда:

• Квантован (т.е. кратен элементарному заряду )

• Аддитивен

• Является скаляром

• Является релятивистским инвариантом (инвариантен относительно преобразований Лоренца).

• Ед.измерения заряда = Кулон (производная единица) 1 Кл = 1 А с (1 А – сила тока, при которой…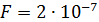 Н)

Модельные представления классической электродинамики о распределении зарядов

Непрерывное распределение зарядов

• – понятие физически бесконечно малого заряда

<< некоторой характерной величины зарядов задачи, но >>

• ‑понятие физически бесконечно малого объема; размеры << характерных размеров задачи

• – объемная плотность непрерывного распределителя зарядов

– поверхностная плотность зарядов

– линейная плотность зарядов

• В общем случае .

Кусочно-непрерывное распределение зарядов (граничные условия)

;

Система точечных зарядов

• «Точечный заряд» = заряд с нулевыми размерами, описываемый микроскопической плотностью , где ‑ Дельта функция Дирака.

‑ радиус‑вектор места расположения i-го заряда.

• Микроскопическая объемная плотность системы точечных зарядов (микроскопических зарядов)

Полный заряд

«Макроскопическая» плотность получается из микроскопической с помощью процедуры огрубления

Модельные представления о распределении токов

Элементарный ток точечного заряда

Микроскопическая плотность тока

Макроскопическая непрерывная плотность тока получается с помощью огрубления

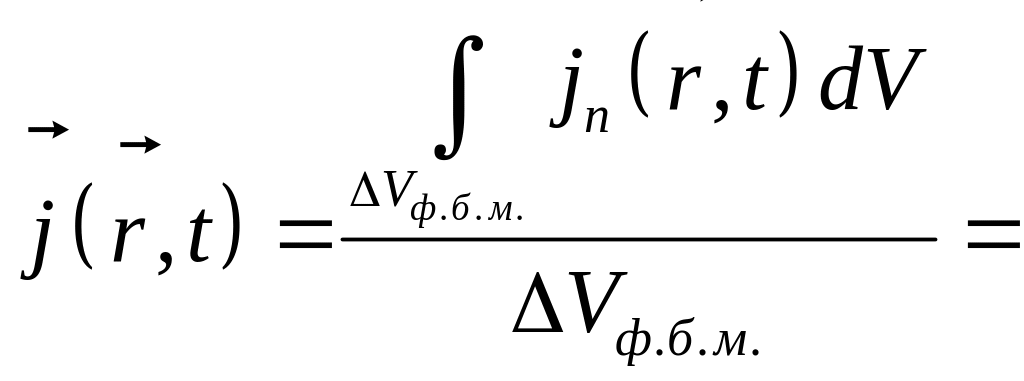
Макроскопическая плотность тока одиноименных зарядов e определяется соотношением

, где

,

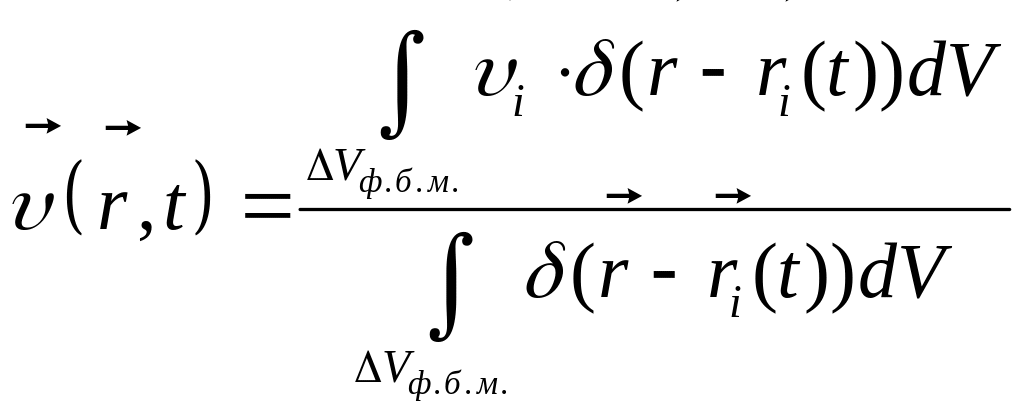Количественной характеристикой электрического тока через поверхность S является величина, называемая силой тока, которая определяется соотношением:

,

где , – нормаль к элементу поверхности, площадью .

Закон сохранения заряда

Наряду с фундаментальными законами сохранения энергии, импульса, момента импульса – (точные законы) + во всех физических процессах выполняется закон сохранения заряда:

При любых известных взаимодействиях элементарных частиц сумма электрических зарядов до и после взаимодействия одинакова.

В классической электродинамике:

В изолированной системе электрический заряд сохраняется.

В изолированной системе изменение заряда определяется током, из системы или в систему. Интегральная формулировка закона сохранения заряда имеет вид

,

где Q – заряд, I – сила тока через поверхность, – нормаль интегральной формулы закона сохранения заряда.

При фиксированной границе

;

Кроме того

.

Отсюда

Это дифференциальная формулировка закона сохранения заряда = уравнение непрерывности

При стационарном распределении зарядов заряды движутся по замкнутым трубкам (в случае непрерывного распределения) или по замкнутым орбитам (в случает точечных зарядов).

Электромагнитное поле. Напряженность электрического поля. Индукция магнитного поля.

• ЭМ поле – основной объект изучения в электродинамике.

• Отличие полевой и вещественной форм материи: взаимопроникновение полей с одной стороны и невозможность помещения (внедрения) тел в одну и ту же область пространства без изменения их свойств.

• Единство материи = применимость понятий к веществу и полю, для которого они непрерывно распределены по пространству с определенной плотностью. При взаимодействии вещества и поля изменяются их ^.

• Исходным для описания ЭМ поля является силовое действие. Различают две составляющие силы

(1) электрическую , действующую на заряд независимо от скорости

(2) магнитную пропорциональную как q так и скорости движения заряда .

Напряженность электрического поля, _-поле, ‑характеризует только силовое действие данного поля (= сила, действующая на единичный положительный заряд, разная в разных полях)

Магнитная индукция, _{-поле, –} характеризует магнитное поле, действующее на движущийся заряд. В общем случае на заряд, помещенный в ЭМ поле, действует сила Лоренца.

Единицы и :

1 ;

При измерениях различают заряды, создающие поле, и пробный заряд.

Формулы для , – по существу представляют собой определения и .

Плотность силы Лоренца

Квазилинейными токами называются токи, поперечные размеры которых пренебрежимо малы по сравнению с длиной. Бесконечно малый участок квазилинейного тока, характеризуется вектором , где – элемент квазилинейного проводника. Пренебрегая изменением вектора плотности тока в пределах поперечного сечения проводника , где нормаль к поперечному сечению квазилинейного проводника параллельна оси проводника и вектору плотности тока , силу тока можно представить в виде

.

Или, вводя элемент объема , можно записать

.

Сила Ампера.

Исходя из выражения для магнитной составляющей силы Лоренца

и предыдущего соотношения, получаем выражение для силы Ампера, действующей на элемент квазилинейного проводника с током

.

ЭМ поле определено, если известно значение двух величин и .

Если = ; = ‑ поле стационарно

Если = ; = - поле стационарно и однородно

«Заряды создают поле» = Заряды неразрывно связаны с полем ( но ЭМ поле может существовать и в отсутствие зарядов).

Любопытно: только кулоновское поле – заряды покоятся, кулоновское и постоянное магнитное поля – заряды движутся равномерно, переменное ЭМ поле – заряды движутся ускоренно.

Потенциальное поле

Напомню, что потенциальное поле описывается соотношениями:

1. ‑ дифференциальная формулировка условия потенциальности

( Интегральная формулировка условия потенциальности )

2.

Чтобы удовлетворить условию , можно представить в виде , что после подстановки во второе уравнение приводит к уравнению Пуассона

для скалярного потенциала

Вихревое поле

Описывается дифференциальным уравнениями

• 1) 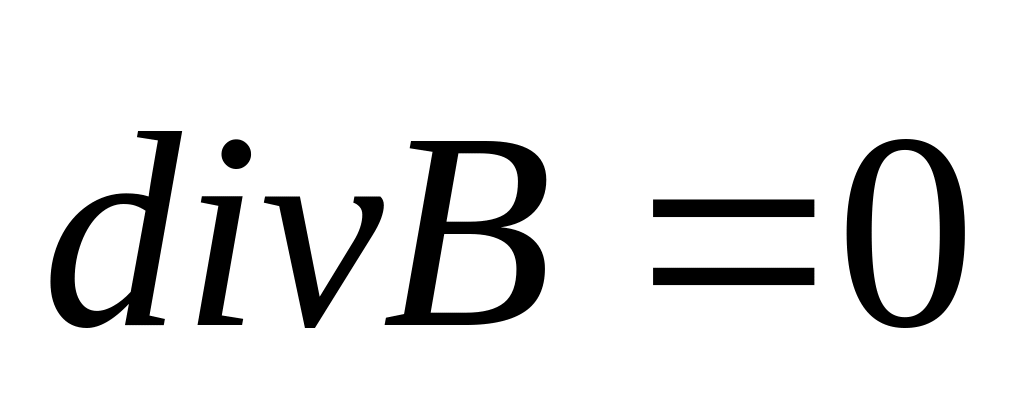‑ дифференциальная формулировка условий соленоидальности

2)

• ‑ интегральная формулировка условия соленоидальности

Первое уравнение удовлетворяется с помощью введения векторного потенциала

Подстановка во второе уравнение с учетом первого приводит к уравнению Пуассона для векторного потенциала.

В общем случае поле можно представить в виде суммы потенциальной и вихревой составляющих: Например , тогда уравнения, описывающие произвольное поле имеет вид:

;

Отсюда следует, что ЭМ поле, состоящее из двух полей – электрического и магнитного – должно описываться двумя парами таких уравнений.

И действительно система уравнений Максвелла состоит из четырех уравнений.

Система уравнений Максвелла (СУМ) для ЭМ поля в вакууме.

С исторической точки зрения СУМ является обобщением элементарных законов электромагнетизма. С точки зрения теоретического описания ЭМ явлений СУМ играет роль исходных теоретических принципов, позволяющих дать классическое описание любых макроскопических ЭМ явлений.

В системе единиц СИ СУМ для ЭМ поля в вакууме имеет вид

I.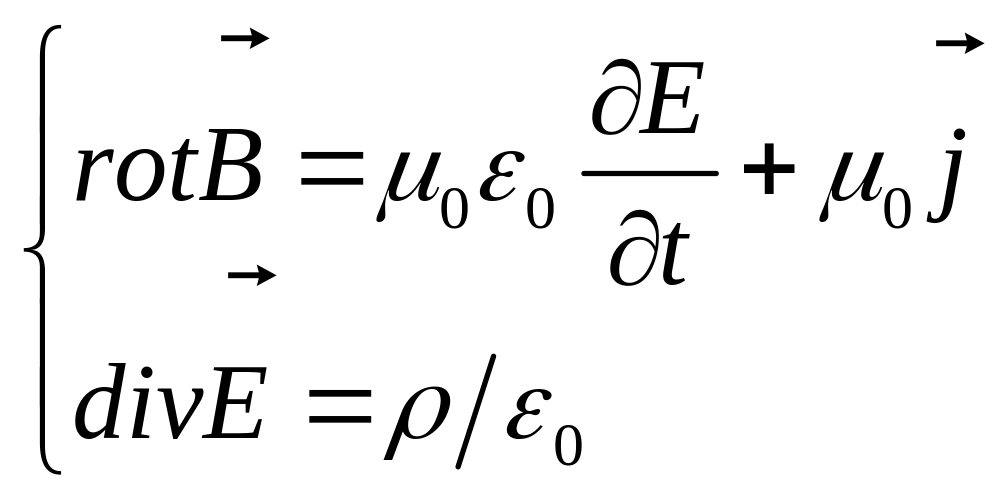 – пара уравнений с источниками поля

II. – пара уравнений без источников поля

Дома :

1) найти размерность из (I.1) с учетом и закона Кулона;

2) убедиться прямым расчетом, что , где ‑ скорость света в вакууме.

Связь между уравнениями Максвелла. (Обобщение статических соотношений на динамику).

Справедливы формулы

1)

С учетом уравнения непрерывности это дает

Если , как это имеет место в электростатике, то это равенство выполняется и в динамике т.к. .

С другой стороны, используя (I.2) из СУМ можно получить закон сохранения заряда.

2) – постоянная во времени, а т.к. - произвольное переменное поле, то - может быть только нулем(?)

Графическое изображение полей

Для наглядности электрическое и магнитное поле часто изображаются силовыми линиями, которые определяются таким образом, что вектор (или ) направлен по касательной к ним в каждой точке пространства. Математическое определение этих линий дается условием коллинеарности вектора (или ) и

или _.

Принцип суперпозиций полей.

При наличии нескольких источников ЭМ поля возникает вопрос о связи между результирующим полем и полем отдельных источников.

С математической точки зрения уравнения Максвелла представляет собой линейные дифференциальные уравнения в частных производных первого порядка.

Линейность уравнений Максвелла является математическим выражением принципа суперпозиции, которому подчиняется ЭМ поле:

векторы и результирующего ЭМ поля равны алгебраической сумме векторов составляющих полей:

.

Важнейшим приложением принципа суперпозиции является представление ЭМ поля в виде разложения по системам ортогональных функций, например, по плоским волнам.

Виды задач, решаемых электродинамикой

Основная задача электродинамики

Решение сводится к отысканию полей и по заданным источникам и .

Сначала находится общее решение СУМ, содержащее некоторые произвольные функции. Решение конкретной задачи находится с помощью определения этих произвольных функций из заданных начальных и граничных условий.

• Начальные условия это заданные значения поля

в некоторый момент времени, принимаемый за начальный (t=0).

• Граничные условия это заданные значения поля

во всех точках некоторой поверхности s – «границы».

• В пустоте отсутствуют какие-либо выделенные поверхности. Поэтому под «граничными условиями» понимают характер поведения поля при удалении от системы зарядов.

Точный физический смысл имеют задачи, в которых источники поля занимают ограниченную область пространства. Граничные условия в этом случае сводятся к требованиям определенного характера затухания поля при бесконечном удалении от источников поля

_.

• Рассматриваемые далее бесконечные системы зарядов: бесконечные нити, поверхности (зарядов и токов) и т.д. являются полезными идеализациями и с физической точки зрения требуют специального исследования.

Обратная задача ЭД (а именно отыскание распределения зарядов и токов по заданному ЭМ полю) в основном сводится к дифференцированию известных функций . Но для нахождения точечных, линейных или поверхностных источников поля используется интегральная формулировка СУМ.

Задача о движении зарядов в заданном поле – это чисто механическая задача, решаемая с помощью второго закона Ньютона в виде

_.

Задача об излучении ЭМ волн сводится к нахождению ЭМ поля, создаваемого заданным движением зарядов.

Задача о рассеянии ЭМ волн сводится к двум предыдущим:

на первом этапе решается механическая задача о движении зарядов в заданном ЭМ поле.

на втором этапе находится вторичное ЭМ поле, создаваемое заданным движением зарядов, которое накладывается на первичное поле.

Уравнение Максвелла-Лоренца

1.Допустим, что имеется изолированная макроскопическая система зарядов и ЭМ поля в вакууме, рассматриваемая на протяжении таких интервалов времени, за которые заряды и поле не выходят за пределы некоторого конечного объема V.

2.Предположим, что мы имеем механические модели тел, несущих электрические заряды. В простейшем случае это свободные материальные точки массой m_i, расположенные в точках . Тогда СУМ для ЭМ поля в вакууме приобретают вид

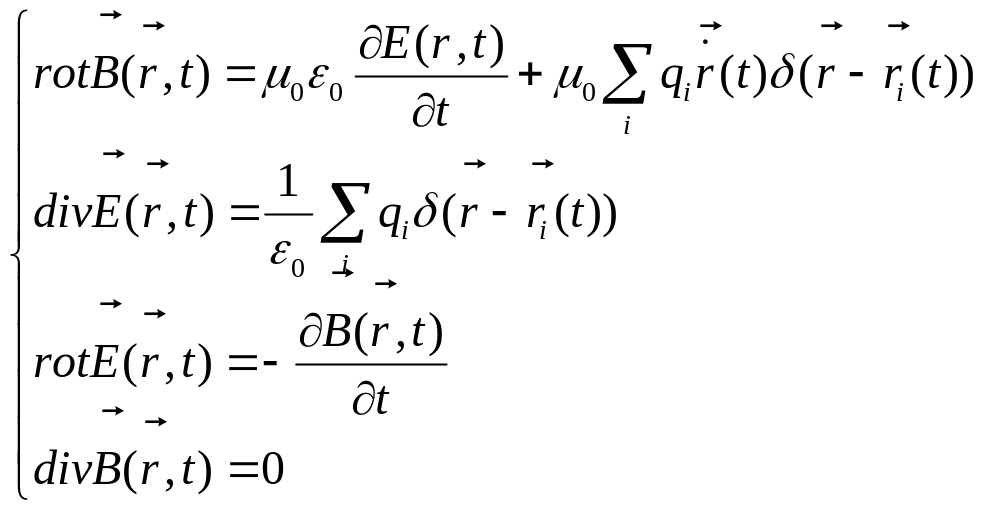
Уравнения движения зарядов в отсутствие сил не ЭМ природы имеют вид

_.

Совокупность этих уравнений называется системой уравнений Максвелла-Лоренца (СУМ-Л).

В принципе она позволяет определить состояние системы в любой момент времени по начальным условиям. Это значит, что в ЭД справедлив принцип причинности.

На этом основании считается, что ЭД является теорией с динамическими закономерностями. Действительно, …определение динамической системы.

Вообще говоря, на тела, несущие заряды, могут действовать силы и не ЭМ происхождения (например, гравитационные, химические и др.), которые не описываются законами классической ЭД. Эти силы получили в ЭД название сторонних сил. При этом поле зарядов по-прежнему определяется СУМ.

В этом смысле постановка проблемы в СУМ шире, чем в СУМ-Л.