
- •Контрольная работа №1
- •Вариант 1
- •Вариант 2
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Вариант 31
- •Вариант 32
- •Вариант 33
- •Вариант 34
- •Вариант 35
- •Вариант 36
- •Вариант 37
- •Вариант 38
- •Вариант 39
- •Вариант 40
- •Вариант 41
- •Вариант 42
- •Вариант 43
- •Вариант 44
- •Вариант 45
- •Вариант 46
- •Вариант 47
- •Вариант 48
- •Вариант 49
- •Вариант 50
- •Вариант 51
- •Вариант 52
- •Вариант 53
- •Вариант 54
- •Вариант 55
Контрольная работа №1
(1- курс)
Вариант 1
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы а(1; 2; 3), b(-1; 3; 2), c (7; -3; 5) и d(6; 10; 17) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4 : A1 (4; 2; 5), A2 (0; 7; 2), A3 (0; 2; 7), A4 (1; 5; 0).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Найти
производные
 данных функций.
данных функций.
а) |
б)
|
в)
|
г)
|
д)
Задание 5.
Найти
и
а) у = x / (x2-1); б) x = cos (t / 2); y = t – sin t.
|
Задание 6.
Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f
(x)
=
 .
.
Задание 7.
Прямоугольник вписан в эллипс с осями 2а и 2в. Каковы должны быть стороны прямоугольника, чтобы его площадь была наибольшей?
Вариант 2
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы а(4; 7; 8),b (9; 1; 3),c(2; -4; 1) и d(1; -13; -13) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4: A1(4; 4; 10),A2(4;10; 2), A3 (2; 8; 4), A4 (9; 6; 4).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Найти производные данных функций:
а)
в)
г)
д)
Задание 5. Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t). а) у = ln ctg2x; б) x = t3 + 8t; y = t5 +2t. Задание 6. Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f
(x)
=
Задание 7. Равнобедренный треугольник, вписанный в окружность радиуса R, вращается вокруг прямой, которая проходит через его вершину параллельно основанию. Какова должна быть высота этого треугольника, чтобы тело, полученное в результате его вращения, имело наибольший объем?
Вариант 3 Задание 1. Дана система линейных уравнений
Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления. Задание 2. Даны векторы а(8; 2; 3), b(4; 6; 10), c (3; -2; 1) и d (7; 4; 11) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе. Задание 3. Даны координаты вершины пирамиды А1А2А3А4 :A1 (4; 6; 5), A2 (6; 9; 4), A3 (2; 10; 10), A4 (7; 5; 9). Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж. Задание 4. Найти производные данных функций.
Задание 5. Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t). а) у = x3 ln x; б) x = t – sin t; y = 1 – cos t.
Задание 6. Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в]. f (x) = . Задание 7. Прямоугольник вписан в эллипс с осями 2а и 2в. Каковы должны быть стороны прямоугольника, чтобы его площадь была наибольшей?
Вариант 4
|
Задание 1.
Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления.
Задание 2.
Даны векторы a(10; 3; 1), b(1; 4; 2), c(3; 9; 2) и d (19; 30; 7) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе.
Задание 3.
Даны координаты вершины пирамиды А1А2А3А4: A1 (3; 5; 4), A2 (8; 7; 4), A3 (5; 10; 4), A4 (4; 7; 8).
Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
Задание 4.
Найти производные данных функций.
а)
|
|||||||
б)
|
|||||||
в)
|
|||||||
г)
|
|||||||
д)
Задание 5. Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).
а)
у = xe-x Задание 6. Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f
(x)
=
Задание 7. Требуется изготовить открытый цилиндрический бак данного объема. Стоимость квадратного метра материала, идущего на изготовление дна бака, равно р1 руб., а стенок р2 руб. Каковы должны быть радиус дна и высота бака, чтобы затраты на материалы для его изготовления были наименьшими?
Вариант 5 Задание 1. Дана система линейных уравнений
Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления. Задание 2. Даны векторы a (1; 2; 3), b (2; -3; 1), c (-1; 2; 1), d (2; 2; 8)в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе. Задание 3. Даны координаты вершины пирамиды А1А2А3А4:A1 (6; 6; 2), A2 (5; 4; 7), A3 (2; 4; 7), A4 (7; 3; 0). Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2 ; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж. Задание 4. Найти производные данных функций.
Задание 6. Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f
(x)
=
Задание 7. Найти радиус основания и высоту конуса наименьшего объема, описанного около шара радиуса R.
Вариант 6 Задание 1. Дана система линейных уравнений
Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления. Задание 2. Даны векторы a (4; 2; 5), b (-3; 5; 6), c (2; -3; -2), d (8; 11; 13) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе. Задание 3. Даны координаты вершины пирамиды А1А2А3А4: A1 (3; 3; 4), A2 (6; 9; 1), A3 (1; 7; 3), A4 (8; 5; 8). Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж. Задание 4. Найти производные данных функций.
Задание 5. Найти и для заданных функций: а) у = f (x); б) x = (t), у = g(t). а) у = ectg3x; б) x = 3 cos t ; y = 4 sin2 t.
Задание 6. Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f
(x)
=
Задание 7. При каких линейных размерах закрытая цилиндрическая банка данной вместимости, будет иметь наименьшую полную поверхность?
Вариант 7 Задание 1. Дана система линейных уравнений
Доказать её совместность и решить двумя способами: 1) Методом Гаусса; 2) средствами матричного исчисления. Задание 2. Даны векторы a (1; 3; 2), b (3; -1; 5), c (-6; 5; -3), d (12; -10; 6) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе. Задание 3. Даны координаты вершины пирамиды А1А2А3А4 : A1 (1; 8; 2), A2 (5; 2; 6), A3 (5; 7; 4), A4 (4; 10; 9). Найти:1)длину ребра А1А2; 2)угол между ребрами А1А2 И А1А4; 3)угол между ребром А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5)объем пирамиды; 6)уравнение прямой А1А2 ; 7)уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж. Задание 4. Найти производные данных функций.
|
Задание 5.
Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).
а) у = ex cos x; б) x = 3 t – t3; y = 3 t3.
Задание 6.
Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f
(x)
=
 .
.
Задание 7.
Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен а. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света?






 для заданных функций: а) у = f
(x);
б) x
=
для заданных функций: а) у = f
(x);
б) x
=
 (t),
у =
(t).
(t),
у =
(t).


 .
. .
.



 ;
;



 ;
;
 ;
б) x
= ln
t;
y
=
;
б) x
= ln
t;
y
=
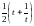 .
.






 .
.





 .
.



 ;
;