Обратимся к системе "идеальный газ". Запишем I закон термодинамики для изохорического процесса:

(6)

Внутренняя энергия идеального газа есть функция только температуры (при неизменной массе).

Разберём изобарический процесс с идеальным газом. Для этого процесса теплота запишется . Для записи изменения внутренней энергии используем формулы (6). Тогда по I закону термодинамики

.

В соответствии с уравнением состояния (5) величина pdV при постоянстве p перепишется как . И из последнего равенства получается

C_p = C_V + R. (7)

Таким образом, с помощью I закона термодинамики и уравнения состояния идеального газа удалось получить полезную формулу, выражающую соотношение между теплоёмкостями C_p и С_V (оно называется соотношением Майера).

Работа при длительном изобарическом процессе может быть записана как

A = p(V₂ - V₁).

Изотермический процесс с идеальным газом. Для этого процесса

T = const, dT = 0. Изменение внутренней энергии (функции только температуры) равно нулю. Значит, по I закону термодинамики

. (8)

Сообщённая газу теплота идёт на совершение им работы. Это самый подходящий процесс для тепловой машины (если не замечать трудностей обеспечивания многократной повторяемости процесса).

Приведём запись работы и теплоты через наблюдаемые параметры:

.

. (9)

Ещё одним замечательным процессом является адиабатический процесс – процесс без теплообмена с окружающей средой. На практике адиабатическими можно считать такие процессы, когда за характерное время процесса система не успевает получить заметное количество тепла (по сравнению, например, с работой). Критерий отсутствия теплообмена должен учитывать и теплоизоляционные качества стенок и быстроту протекания процесса. Даже в случае, казалось бы, плохих теплоизоляционных характеристик стенок процесс является адиабатическим, если протекает достаточно быстро. Примерами адиабатического процесса являются: быстрое расширение газа при кратковременном вытекании некоторой порции его через малое отверстие; быстрое сжатие горючей смеси в цилиндре двигателя внутреннего сгорания; периодические сжатия и расширения вещества в поле звуковой волны.

Быстрые адиабатические процессы могут считаться квазистатическими, если при сравнительно малых экстенсивных параметрах системы время релаксационных процессов в ней пренебрежимо мало по сравнению с характерным временем процесса.

Выясним, каковы соотношения между наблюдаемыми параметрами при квазистатическом адиабатическом процессе с идеальным газом. По I закону термодинамики .

С помощью уравнения состояния (4) выразим dT через p, V, dp, dV :

.

Подставив dT в I закон термодинамики, получим

.

Так как C_V + R = C_p, то далее удобно ввести константу , называемую адиабатической постоянной. И тогда , откуда далее

. (10)

Уравнение (10) называется уравнением Пуассона. Его можно переписать в переменных V,T или p,T :

. (10^l)

. (10^ll)

Уравнение Пуассона говорит о связи между изменениями каких-либо двух параметров, хотя при адиабатическом процессе меняются все три параметра V, p, T . На диаграмме V – p график адиабатического процесса (кратко, адиабаты) представляет собой гиперболу класса . Адиабата всегда идёт круче изотермы.

Как записать работу при адиабатическом процессе с идеальным газом? Исходим из формулы . Для неэлементарного процесса 1 – 2

.

Наиболее доступной для наблюдения величиной является объём. В последней записи отношение температур с помощью формулы (10^l) выразим через отношение объёмов, а для преобразования величины воспользуемся соотношением Майера и уравнением состояния:

;

. (11)

Все рассмотренные выше процессы относятся к политропическим процессам. Для всех политропических процессов соблюдается постоянство теплоёмкости (она не меняется в ходе процесса). Общее уравнение политропического процесса pVⁿ = const, где n – число (целое или дробное).

Э н т р о п и я –– ф у н к ц и я с о с т о я н и я с и с т е м ы

Будем иметь в виду систему – идеальный газ. Рассмотрим величину при квазистатическом, а значит, и при обратимом процессе:

Правую часть можно представить как дифференциал некоторого выражения, а именно: . В выражение в квадратных скобках входят параметры состояния, а значит, и само выражение есть функция состояния. Последнее утверждение можно обобщить на произвольную систему (обобщение такое составляет содержание теоремы Карно). Таким образом, при обратимых процессах величина есть дифференциал некоторой функции состояния S. Эта функция была названа энтропией (по Клаузиусу).

(12)

Запишем формулу изменения энтропии для процесса 1 – 2 с идеальным газом:

. (13)

Мерой чего является энтропия? Энтропия есть мера хаотичности теплового движения. Это можно увидеть из таких примеров.

Пример 1. Плавление кристаллического тела, когда системе сообщается тепло при некоторой постоянной температуре, и в соответствии с формулой (12) энтропия увеличивается. Известно, что при плавлении движение атомов и молекул становится гораздо более неупорядоченным. Только с этим и можно связать изменение S.

Пример 2. Изотермическое расширение идеального газа от объёма V₁ до объёма V₂ > V₁. Здесь в соответствии с формулой (13) изменение энтропии положительно, а молекулам газа предоставляется больший объём, то есть "большая свобода", "больший оперативный простор". Степень неупорядоченности увеличивается и только с этим можно связать увеличение энтропии. Можно привести и другие подобные примеры.

З а к о н в о з р а с т а н и я э н т р о п и и

Энтропию как меру хаотичности теплового движения можно приписывать как равновесным, так и неравновесным состояниям. Как меняется энтропия при некотором необратимом процессе в изолированной системе, когда она "самостоятельно" переходит от состояний, далёких от равновесия, к состояниям, близким к равновесию и в конце концов к равновесию? Обратимся опять к примерам.

Пример 3. В начальном состоянии имеются две разделённые половинки стержня. Температура левой половинки T₁, температура правой половинки

T₂ < T₁ . Далее половинки приводятся в контакт через вспомогательную узкую прослойку, теплопроводность которой гораздо меньше теплопроводности материала стержня. Путём теплопроводности через прослойку происходит выравнивание температур, когда температура каждой половинки будет T = 0,5(T₁ +T₂). Процессы нагревания правой половинки и охлаждения левой половинки можно считать квазистатическими и обратимыми. За необратимость процесса во всей системе 1 + 2 отвечает контакт между половинками.(узкая прослойка). Изменение энтропии можно представить как сумму изменения энтропии в первой половинке и изменения таковой во второй половинке, то есть

.

.

Так как T²/T₁T₂ = (T₁ + T₂)²/4T₁T₂ > 0, то .

Пример 4. Идеальный газ расширяется в пустоту в условиях механической и тепловой изоляции (рис. 23). Вначале газ находился в объёме V₁, ограниченном перегородкой A. По другую сторону от перегородки никакого газа нет (вакуум). После резкого удаления перегородки газ занимает объём V₂ > V₁. Расширение происходит без совершения работы и без теплообмена. Поэтому внутренняя энергия не меняется, а следовательно, не меняется температура. При подсчёте изменения энтропии мы можем принять, что состояние 1 (V = V₁) есть конечное состояние обратимого зотермического расширения от некоторого начального объёма V₀ до объёма V₁ > V₀, а состояние 2 (V=V₂) – конечное состояние обратимого изотермического расширения от V₀ до V₂. Согласно формуле (13) разность энтропий в состояниях 2 и 1 можно представить так:

Рис. 23

.

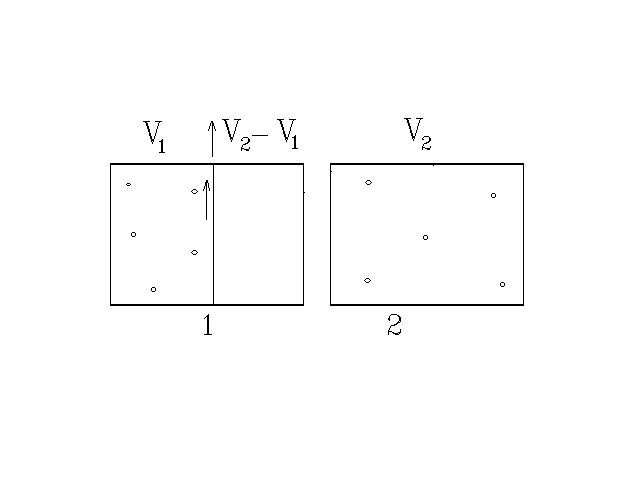
Рассмотренные примеры позволяют сделать обобщение: В замкнутых изолированных системах энтропия не убывает:

. (14)

Если в полностью изолированной системе отсутствуют процессы (система в своём равновесии), то энтропия не меняется. Если же в системе идут необратимые процессы, а в замкнутых изолированных системах возможны только такие, то энтропия возрастает. Короче, в таких системах энтропия стремится к максимуму.

II з а к о н т е р м о д и н а м и к и и к. п. д. т е п л о в ы х м а ш и н

Утверждение, выражаемое записью (14), есть одна из формулировок II закона термодинамики. Другие формулировки II закона термодинамики (классические) читаются так:

Невозможен двигатель, который периодически забирал бы из одного теплового резервуара некоторое количество тепла и полностью превращал бы его в работу без каких-либо изменений в окружающих телах (формулировка Томсона- Кельвина);

Невозможен самопроизвольный переход тепла от тела с меньшей температурой к телу с большей температурой без каких-либо изменений в окружающих телах (формулировка Клаузиуса).

Тепловой двигатель, упомянутый в формулировке Томсона-Кельвина, называют вечным двигателем II рода. Невозможен вечный двигатель II рода – это уже формулировка Планка.

Все приведённые формулировки равносильны. В своё время формулировки II закона термодинамики появились в связи с вопросом о к.п.д. тепловых машин. В тепловых машинах система периодически должна совершать работу над внешними телами. Это значит, что система периодически должна возвращаться в начальное состояние 1 (рис. 24), причём возвращаться иным путём, нежели при удалении из состояния 1 (чтобы работа над системой при возвращении её была меньше работы системы над внешними телами при удалении её из состояния 1). То есть система совершает замкнутый процесс – цикл. За цикл совершается в целом положительная работа A, которая численно равна площади фигуры цикла. Это ясно видно, если используется диаграмма V – p. На какой- то части цикла система получает тепло Q₁ от одних внешних тел – нагревателя (на рис. 24 участок a). На другой части цикла система отдаёт некоторое количество тепла Q₂ (рис. 24, участок b). Как можно убедиться с помощью формулировок II закона, получать тепло от системы должны уже другие тела – холодильник. По I закону термодинамики для цикла

Q

Рис. 24

= Q₁ - Q₂ = A, (15)

так как изменение внутренней энергии за цикл равно нулю. Работа A считается полезной величиной, теплота нагревателя Q₁ считается затратами. К.п.д. цикла (т.е. к.п.д. тепловой машины) будет

. (16)

Как II закон термодинамики помогает делать суждения о к.п.д. тепловой машины при конкретных холодильнике и нагревателе и как "перекликаются" между собой разные формулировки II закона термодинамики, разберём всё это на следующем примере. Пусть имеются два массивных тела с температурами T₁ и T₂ < T₁ соответственно (рис. 25). В дальнейшем будем их называть термостатами. Ещё тело 1 можно назвать нагревателем, тело 2 –– холодильником. Если бы не было тела 2 (холодильника), получить работу с помощью одн

Рис. 25

ого первого тела было бы невозможно. Об этом прямо говорит формулировка Томсона – Кельвина. С точки зрения энтропии система (тело 1) находится в равновесии, энтропия максимальна, процессы возникнуть не могут (энтропия не может убывать). Большая система из двух тел 1 и 2 является в принципе неравновесной, так как температуры её частей разные. В этой системе «можно спровоцировать» процессы и получить работу. Простой контакт тела 1 с телом 2 ничего не даст. Будет необратимый процесс теплопроводности подобно процессу в примере 1. Работа не совершается (нет перемещений стенок). Нужно поступить более разумно – ввести рабочее тело, которое поочередно то контактирует с телом 1, то не контактирует ни с каким телом, то контактирует с телом 2. Лучше всего роль рабочего тела выполняет газ, так как он заметно меняет свой внешний параметр – объём. Работа, совершаемая рабочим телом, будет тем больше, чем меньше мы допустим какие-либо необратимые процессы. Самый лучший случай – случай, когда необратимые процессы вовсе исключены. Это значит, что при контакте рабочего тела с термостатом 1 температура рабочего тела должна быть T₁ , а при контакте его с термостатом 2 температура должна быть T₂. Когда рабочее тело не контактирует ни с одним термостатом (изолировано), температура его меняется между значениями T₁ и T₂.. Таким образом, самый выгодный цикл с рабочим телом в случае термостатов с постоянными температурами T₁ и T₂ должен состоять из двух изотерм и двух адиабат (рис. 26). Такой цикл называется циклом Карно. К.п.д. тепловой машины, работающей с нагревателем, постоянная температура которого T₁, и холодильником, постоянная температура которого T₂, будет максимально возможным, если цикл рабочего тела есть цикл Карно. Выделенное предложение есть содержание теоремы Карно. Легко составить формулу для к.п.д. цикла Карно. В соответствии с ф

Рис. 26

ормулой (12) для обратимых процессов можно записать (см. рис. 26):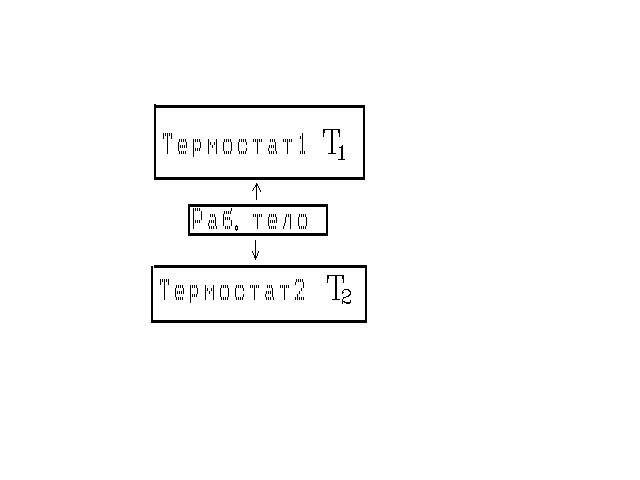

И к.п.д. цикла Карно будет

. (17)

м о л е к у л я р н о – к и н е т и ч е с к а я

т е о р и я

Поведение макроскопических тел изучается ещё молекулярно–кинетической теорией (МКТ). Другое название этой теории – физическая статистика (статистическая физика). Здесь макроскопические свойства тел объясняются с помощью представлений об атомно–молекулярной структуре вещества. Основные положения молекулярно–кинетической теории следующие.

1. Тела состоят из множества микрочастиц –– атомов и молекул, находящихся в беспрестанном хаотическом движении.

2. В течение большого промежутка времени поведение частиц или даже групп частиц подчиняется статистическим закономерностям.

3. Статистические закономерности можно описать с помощью некоторых функций распределения.

4. Любой макроскопический параметр системы есть статистически среднее от некоторой микроскопической величины. Подсчёт статистически среднего проводится с помощью функций распределения.

Положения 1 и 2 являются обобщением всего опыта, накопленного наукой и практической деятельностью. В чём заключаются статистические закономерности? Поведение одной частицы в течение большого промежутка времени (когда на её движение повлияли много других частиц) выглядит настолько замысловатым и запутанным, что, казалось бы , трудно о нём сказать что–то определённое. Однако это как раз позволяет сделать утверждение (чуждое духу детерменизма): частица за большое время обязательно побывает в любом наперёд заданном состоянии, в каких–то состояниях она побывает чаще, в каких–то состояниях – реже. Как можно пояснить положение 4? Например, давление газа есть статистически среднее от такой микроскопической величины как импульс, передаваемый единице площади стенки за единицу времени.

Максвелловское распределение молекул по скоростям. Статистические закономерности поведения макросистемы можно описать с помощью функций распределения. Одной из таких функций, причём важнейших функций, является функция, описывающая распределение молекул по скоростям (распределение Максвелла). Доля молекул dN(v)/N, величины скорости которых имеют значение v в пределах dv, пропорциональна интервалу dv и, кроме того, есть функция v:

(18)

Здесь k = R/N_A – постоянная Больцмана; – постоянная; m – масса молекулы; N_A – число Авогадро.

Самым главным (ответственным) множителем здесь является множитель

, (19)

называемый функцией Максвелла. Множитель можно истолковать как элемент объёма в скоростном пространстве (пространстве, где осями являются v_x, v_y, v_z ). С помощью распределения Максвелла можно найти среднее значение величины, являющейся функцией скорости. Например: средняя скорость <v> , средний квадрат скорости <v²> . Процедура подсчёта средних такова:

(20)

Для средней скорости и среднего квадрата скорости формула (20) перепишется:в виде

(21)

. . (22)

Опираясь на формулу (22), можно записать формулу для средней кинетической энергии молекулы, если последнюю считать материальной точкой:

. (23)

Наряду со средней скоростью <v> и среднеквадратичной скоростью (<v²>)^1/2 часто требуется знать так называемую вероятную скорость v_P. Это значение скорости, соответствующее максимуму выражения dN/Ndv. Такая скорость чаще всего встречается у молекул. Исследуя на максимум множитель перед dv в правой части (17), получим

. (24)

Теплоёмкость идеального газа по классической молекулярно-инетической теории. В формуле (23) для средней кинетической энергии молекула считается материальной точкой, имеющей три степени свободы. Все эти степени свободы равноправны, и поэтому на каждую степень свободы приходится средняя энергия kT/2. Этот результат обобщается на случай, когда молекула не является материальной точкой и имеет дополнительные степени свободы. Это формулируется как теорема о равномерном распределении средней энергии частицы по степеням свободы.

Так в двухатомной молекуле наряду с поступательным движением (три степени свободы) возможны вращательные движения вокруг двух осей, перпендикулярных оси молекулы. А если между атомами молекулы существует упругая связь (расстояние между атомами меняется), то этой связи следует приписать две степени свободы, на каждую из которых приходится средняя энергия kT/2 По теореме о равномерном распределении энергии по степеням свободы на каждую степень свободы (поступательную ли, вращательную ли,) приходится средняя энергия kT/2. Средняя энергия колебательного движения состоит из средней кинетической энергии и средней потенциальной энергии. В случае гармонических колебаний эти энергии равны друг другу и, значит, средняя энергия колебательного движения молекулы равна kT/2 + kT/2 = kT. Теплоёмкость идеального газа определяется тем, сколько степеней свободы и какие именно степени свободы следует приписать молекуле газа.

Если газ одноатомный (He, Ne, Ar ..}, то молекуле следует приписать три поступательные степени свободы. Внутренняя энергия одного моля будет N_AkT/2, где N_A – число Авогадро. В соответствии с этим мольные теплоёмкости C_V , C_p и адиабатическая постоянная будут:

.

Для идеального газа из двухатомных молекул без упругой связи между атомами число степеней свободы равно пяти ( три поступательных и две вращательных). Отсюда для теплоёмкостей и адиабатической постоянной получится:

.

Для газа из двухатомных молекул с упругой связью между атомами число степеней свободы равно семи. Поэтому внутренняя энергия одного моля такого газа будет

N_A(kT/2)(3 + 2 + 2) = (7/2)N_AkT.

Отсюда

.

Минимальное значение C_V трёхатомного газа равно 3R (три поступательные степени свободы и три вращательные). В этом случае молярная теплоёмкости и адиабатическая постоянная будут

Более высокие значения определяются тем, сколько колебательных степеней свободы имеет молекула газа при данной температуре.

Результаты опытов говорят о том, что значение C_V двухатомного газа равно либо 3R/2 (при очень низких температурах), либо 5R/2 (температуры порядка комнатной), либо 7R/2 (при очень высоких температурах). Почему вращательные степени свободы появляются лишь при комнатных температурах и выше, а колебательные степени свободы появляются при очень высоких температурах? Этого классическая молекулярно-кинетическая теория объяснить не может. Эту трудность преодолевает квантовая механика.

Распределение Больцмана. Так как скорость и кинетическая энергия связаны однозначно, то распределение Максвелла можно назвать распределением по кинетическим энергиям. В формуле (17) в показатель степени входит кинетическая энергия, делённая на kT, а множитель v²dv можно переписать через энергию E и dE:.

.

Если система находится во внешнем силовом поле, то частицы наряду с кинетической энергией имеют потенциальную энергию во внешнем силовом поле. Потенциальная энергия отдельной частицы за большое время меняется как случайная величина. Есть все основания считать, что закон случая для потенциальной энергии будет тем же самым, что и для кинетической энергии. Тогда для распределения по потенциальным энергиям можно записать

.

Формула записана по аналогии с формулой (17). Вместо кинетической энергии теперь фигурирует потенциальная энергия U(x,y,z), вместо элемента скоростного объёма – элемент реального пространства dV = dxdydz. При переходе к более удобной записи формулы вводят плотность частиц n = dN/dV и новую константу Nconst = const^l = n₀. Тогда

. (25)

Константа n₀ имеет смысл концентрации частиц в том месте, где потенциальная энергия равна нулю.

Формулу (25) можно применить к молекулам атмосферы Земли, считая их частицами одинаковой массы (), а также к отдельной компоненте смеси газов атмосферы – азоту, кислороду, углекислому газу, водороду и т.д. В этом случае

. (26)

Здесь z – высота над поверхностью Земли.

Чем больше масса молекулы газа, тем быстрее концентрация газа убывает с высотой. На большой высоте состав атмосферы обогащён более лёгкими фрациями и обеднён более тяжёлыми фракциями. Если равенство (26) помножить на kT, причём температура T считается не зависящей от z, а газ считается идеальным, то получится барометрическая формула

. (27)

С помощью этой формулы можно узнавать высоту, сравнивая показания барометра в данном положении с показаниями барометра на уровне Земли.

Я в л е н и я п е р е н о с а , д л и н а с в о б о д н о г о п р о б е г а,

к о э ф ф и ц и е н т ы п е р е н о с а

Релаксационные процессы, как правило являются процессами переноса. Типичными процессами переноса являются диффузия и теплопроводность. При диффузии происходит перенос молекул примеси из мест, где концентрация больше, в места, где концентрация меньше. При теплопроводности происходит перенос средней кинетической энергии из мест, где она больше (т.е., где больше температура), в места, где она меньше. Причём при теплопроводности перенос вещества отсутствует.

Важную роль для процессов переноса в газах играет длина свободного пробега молекулы. Это средний путь, проходимый молекулой за время между двумя последовательными соударениями. Если бы молекулы газа сталкивались не друг с другом, а только со стенками сосуда, то процессы переноса проходили бы чрезвычайно быстро. Скажем, распространение запаха духов в комнате (диффузия примеси) проходило бы за сотые доли секунды, так как средняя скорость молекул при комнатной температуре составляет сотни метров в секунду, а размер комнаты – несколько метров.

Выясним, как длина свободного пробега связана с другими параметрами газа и прежде всего с концентрацией. Можно записать

, (28)

где λ – длина свободного пробега; Z – среднее число столкновений, испытываемых молекулой за одну секунду.

Столкновения молекул происходят потому. что молекулы имеют хотя и малые, но конечные размеры. Будем считать молекулы твёрдыми шариками диаметром d . Чтобы составить выражение для Z, рассмотрим мысленную ситуацию (рис. 27). Выделенная молекула, изображённая на рисунке как жёсткий шар, движется со средней относительной скоростью среди прочих подобных себе неподвижных молекул, изабражённых точками . Если расстояние между линией скорости выделенной молекулы и центром иной молекулы будет меньше 2r = d , то столкновение произойдёт (см. рис. 27). В данном случае площадь «мишени» в виде круга радиусом d есть эффективное сечение столкновения Разумно утверждать, что если на объём цилиндра с площадью основания и образующей

<

Рис. 27

v_отн> 1с приходится одна молекула газа, то выделенная молекула в среднем испытает одно столкновение за одну секунду. Если же на указанный объём приходится Z молекул, то выделенная молекула испытает в среднем Z столкновений за одну секунду. Число молекул в объёме цилиндра будет nS<v_отн>. Тогда для длины свободного пробега (с учётом формулы (28) и формулы <v_отн> = 2^1/2<v>) получается

. (29)

По классическим представлениям длина свободного пробега зависит от концентрации молекул.

Часто важно знать, какова вероятность того, что молекула пройдёт путь x, не испытав столкновения. Не демонстрируя вывод, приведём формулу для этой вероятности:

. (30)

В предельных случаях формула (30) даёт очевидные с точки зрения здравого смысла результаты .

Длина свободного пробега и коэффициенты переноса. Как с длиной свободного пробега связаны коэффициенты переноса – коэффициент диффузии D и коэффициент теплопроводности K?

Феноменологический закон диффузии (первое уравнение Фика) для одномерного случая можно записать так:

, (31)

где dN/dt – число молекул, переносимых в единицу времени через поверхность S, помещённую в точку x и ориентированную перпендикулярно оси x;

n = n (x) – концентрация молекул как функция координаты x.

Феноменологический закон теплопроводности для одномерного случая:

, (31)

где dQ/dt – количество тепла, переносимое в единицу времени через воображаемую поверхность S, помещённую в точку x и ориентированную перпендикулярно оси x; «T» – температура как функция координаты x.

Попытаемся составить выражение dN/dt, исходя из представлений о хаотическом движении молекул газа. Назовём односторонним хаотическим молекулярным потоком число молекул, проходящих справа налево через поверхность S за 1 с. Выражение для этого потока, полученное с помощью распределения Максвелла, имеет вид

,

где v – средняя арифметическая скорость молекулы.

У

Рис. 16

чтём теперь фактор столкновений. Если, скажем, молекулы стартовали из точек на расстоянии x от S (рис. 28), то не все они дойдут до поверхности S и пересекут её. Часть молекул испытает столкновения и потеряется. Поэтому для потока молекул этой категории, стартующих из точек x, через поверхность S, должно быть справедливо выражение

(32)

В этом выражении первый множитель есть в соответствии с формулой

(30) вероятность того, что молекула пролетит путь x без столкновений. Величина есть среднее смещение молекулы вдоль оси x.. Она связана со средней длиной свободного пробега соотношением

. (34)

Множитель 2/3 учитывает то обстоятельство, что не всегда случайный пролёт «средней» молекулы на расстояние бывает в направлении оси x.

Поток молекул всех категорий справа налево через поверхность S есть сумма выражений (33), записанных для всех слоёв dx со всевозможными x. Вклад каждого слоя пропорционален множителю (здесь зависимостью n = n(x) можно пренебречь). Сумма всех таких множителей есть длина свободного пробега, то есть

.

Поэтому долевым вкладом слоя надо считать величину .

Поток справа налево молекул всех x-категорий запишется

.

Перепишем это выражение, применяя интегрирование по частям:

.

Здесь n₀ – концентрация молекул в точке x = 0 (на поверхности S); множитель dn/dx был вынесен за знак интеграла, так как эта величина практически неизменна на интервале x порядка нескольких длин свободного пробега.

При записи встречного потока молекул слева направо мы должны ввести ось x^l , противоположную оси x. Поэтому dn/dx^l = - dn/dx. Тогда для данного потока получится

.

Этот поток больше. чем dN_– /dt_{_}, так как в нашем случае (см. рис. 28)

dn/dx < 0_{_}. Разность потоков dN₊/dt – dN_–/dt и есть диффузионный поток через поверхность S. Для него с учётом соотношения (34) получается выражение

(35)

Сравнивая формулу (35) с формулой (31), видим, что

. (36)

Коэффициент диффузии пропорционален длине свободного пробега.

Нетрудно понять, что и коэффициент теплопроводности K также пропорционален длине свободного пробега. Молекулярный механизм теплопроводности состоит в том, что молекулы при их переходах через поверхность S надо рассматривать как переносчиков средней кинетической энергии (в расчёте на одну молекулу). Чтобы записать энергию, переносимую молекулами категории x (справа налево), надо выражение для dN₊/dt помножить на величину C_VT(x)/N_A. Проделав далее выкладки, аналогичные выкладкам при выводе формулы (35), получим такое выражение для потока тепла:

. (37)

Сравнивая (37) с (32) и учитывая, что

( –– плотность), видим

. (38)

Между коэффициентами K и D существует связь

. (39)

В своё время указание на такую связь было большим успехом молекулярно-кинетической теории газа.