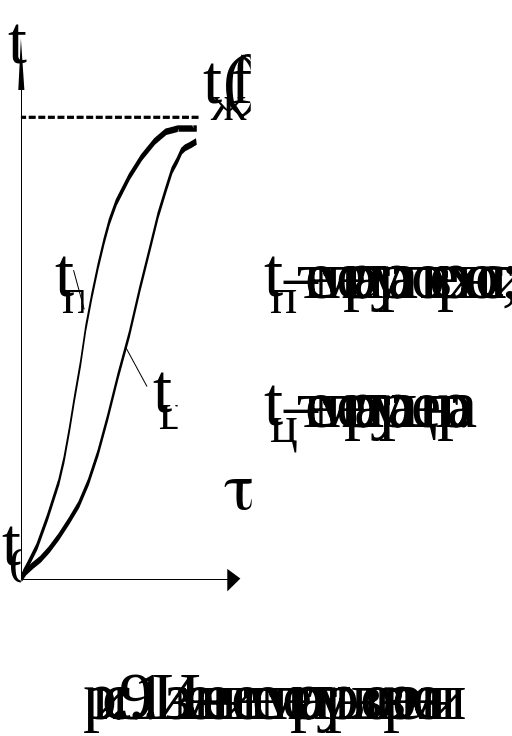
9 Нестационарная теплопроводность. Температурный график нагрева (охлаждения) тела.
Нагрев металла для ковки, штамповки и т.д. в нагревательной и термической печах происходит при нестационарном режиме, т.е. температура (t, С) в металле изменяется не только в пространстве, но и во времени.
По
мере нагрева температура в каждой точке
асимптотически приближается к температуре
греющей среды. Наиболее быстро изменяется
температура по поверхности (
).
Нестационарная теплопроводность
наблюдается и при внезапном изменении
температуры одного из теплоносителей.
В этом случае не вся теплота будет
передаваться через стенку, а часть её
уйдёт на изменение энтальпии (внутренняя
энергия самой стенки), и при наступлении
стационарного режима вся теплота будет
передаваться от одного теплоносителя
к другому. Поэтому нестационарные
процессы теплопроводности связаны с
изменением внутренней энергии или
энтальпии вещества. Нестационарные
режимы теплопроводности могут быть
периодическими или переходными.
Переходные процессы характеризуются
переходом из одного стационарного
состояния в другое, они наиболее часто
встречаются в практике. Периодические
режимы – это такие режимы, при которых
некоторые распределения температуры
повторяются через определённые промежутки
времени.
10 Графики (номограммы) для расчета температуры в центре и на поверхности тел классической формы (неограниченная пластина, бесконечный цилиндр, шар).
Рассмотрим
процесс охлаждения плоской стены
(пластины), толщиной
.
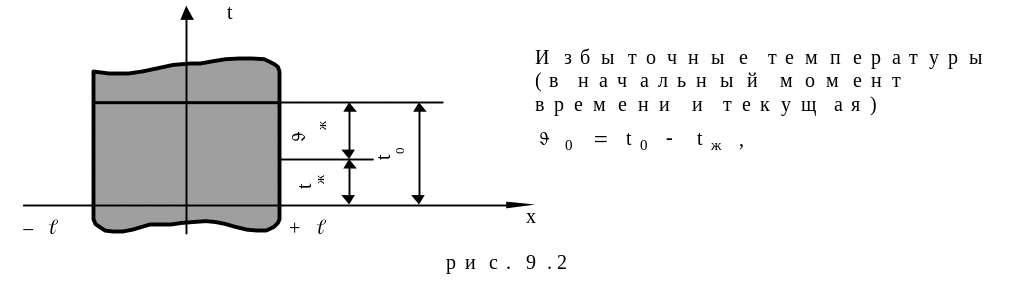
Уравнение однородной стационарной теплопроводности (9.1) для рассматриваемого случая можно записать через избыточную температуру:
. (9.4)
Для решения этого уравнения необходимо иметь краевые условия.
Начальные условия.
1) 
, 
.
.
Граничные
условия: так как плоскость симметрии
пластины проходит через
,
то
2) 
,
при
.
При
на поверхности пластины граничные
условия III-рода:
3) при
.
.
В соответствии с (9.2) общее решение (9.4) будет иметь вид:
. (9.5)
Используя начальные и граничные условия для определения постоянных интегрирования , можно получить трансцендентное уравнение вида:
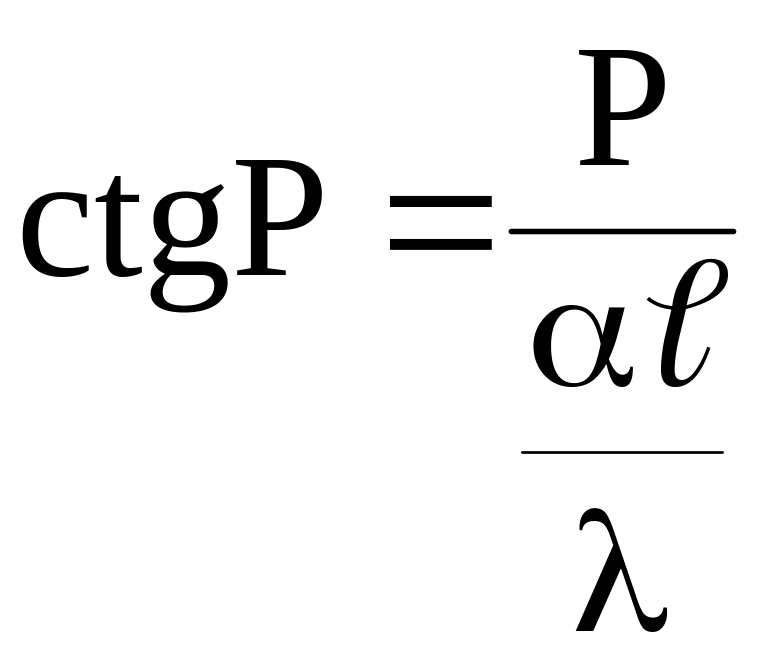, (9.6)
. (9.7)
Уравнение (9.7) наиболее просто решается графически.
Из рисунка 9.3 видно, что имеется бесчисленное множество корней для каждого значения Bi. Найдём границы изменения числа Bi.
Если
Bi,
то при заданном размере стенки
и её материала, в этом случае ;
при этом температуры стенки и жидкости
оказались равными
,
а корни уравнения (9.7) имеют следующие значения
;
;
;
…;
,
.
На
практике
,
это случай когда
.
Если
Bi
0,
0. В этом случае избыточная температура:
,
т.е. теплоотдачи от поверхности пластины
к жидкости нет, и корни уравнения (9.7)
,
где n – порядковый номер корня.
Для каждого значения 0 Bi, решение дифференциального уравнения (9.4) будем искать в виде:
. (9.8)
Определив
,
запишем окончательное решение уравнения
теплопроводности (9.4):
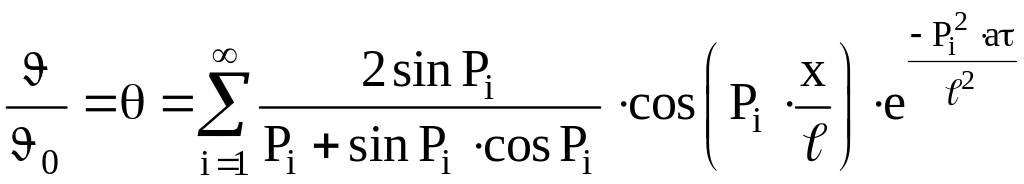(9.9)
(быстросходящийся ряд Фурье)
Решение (9.9) можно представить в обобщённых переменных:
, (9.10)
где 
– безразмерная
координата;
– число
подобия Фурье (безразмерное время).
Решения (9.10) представлены в виде простых и удобных номограмм, которые могут быть двух видов. Номограммы построены для двух случаев:
– центр
пластины
– поверхность
пластины
Зависимость (9.10) справедлива также для цилиндра и шара.
Для
решения прямой задачи определения
температуры в центре либо на поверхности
пластины через какой-то момент времени
после её охлаждения в среде с
,
при заданных размерах
,
материале пластины ,
и
находится
.
Поднимаем до пересечения с нужным Bi и
находим относительную избыточную
температуру, тогда абсолютная температура
в центре будет равна:
.
В любом сечении температура находится с помощью решения (9.9).
Скорость распределения и изменение температуры в теле зависит от отношения поверхности тела к его объёму. Чем больше это отношение, тем больше скорость распространения температуры в теле. Это справедливо для любых значений Bi.
Для
безграничной пластины, цилиндра, шара
при
уравнения температурного поля в
безразмерных координатах:
,
,
.
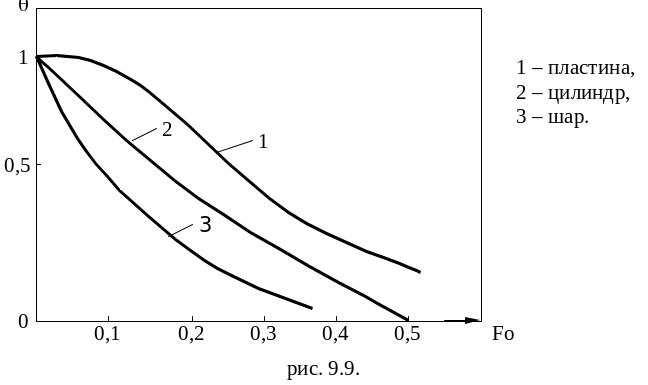
При
одинаковом определяющем размере
и прочих равных условиях
наибольшая скорость изменения температуры
во времени будет наблюдаться для шара.
У него больше отношение поверхности к
объёму.
Если
сравнить отношения поверхности тела к
его объёму для пластины, цилиндра и
шара, то их можно представить:
.