3 Теплопроводность через однослойную плоскую стенку при граничных условиях I-го рода.

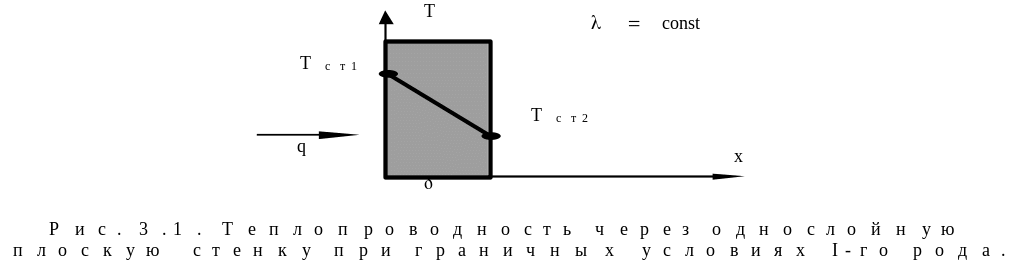
Т.к. процесс стационарный, то температуры на поверхности не меняются во времени и, следовательно, ,

и дифференциальное уравнение теплопроводности будет уравнение Лапласа. Так как температура меняется только вдоль оси ОХ, то для неё:

и .

В этом случае дифференциальное уравнение теплопроводности:

. (3.1)

При , температура ;

при , .

Решаем дифференциальное уравнение (3.1)

,  .

При , ;

при , ;

следовательно, ,

– решение ДУ (3.1). (3.2)

Формула (3.2) описывает распределение температуры в плоской однородной стенке.

Плотность теплового потока определяется согласно закону Фурье:

, (3.3)

Величина называется термическим сопротивлением , .

– тепловая проводимость.

– полный температурный перепад.

Текущий температурный перепад: .

Безразмерный температурный напор обозначим через ,

В безразмерных координатах Уравнение прямой линии имеет вид: . (3.5)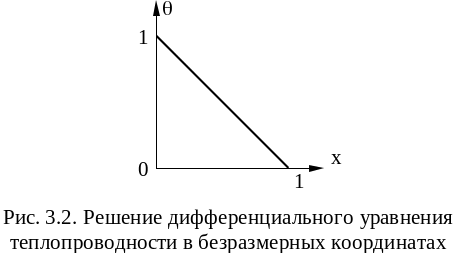

Формула (3.5) – решение уравнения (3.1) в безразмерных координатах.Чтобы найти тепловой поток Q надо по (3.3) определить плотность теплового потока и умножить её на поверхность: Вт.

4 Теплопередача через плоскую однослойную стенку при граничных условиях III-рода

Теплопередача – процесс теплообмена между двумя средами (теплоносителями), разделёнными стенкой (перегородкой). В этом случае при граничных условиях III-рода задаются температуры сред теплоносителей, коэффициенты теплоотдачи между горячей средой и стенкой и между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности и толщина стенки δ.

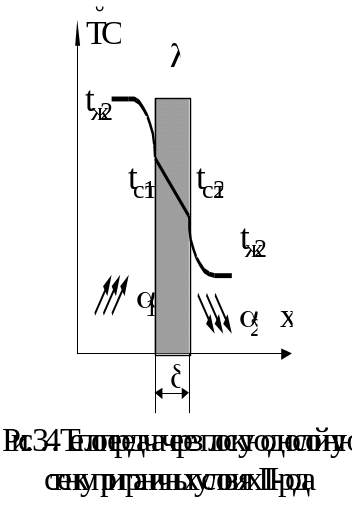
Требуется найти плотность теплового потока, тепловой поток и температуру поверхности стенки.

Согласно закону Ньютона-Рихмана плотность теплового потока между горячей средой и поверхностью стенки: . (3.9)

По закону Фурье этот же поток передаётся теплопроводностью:

. (3.9)

Этот же тепловой поток согласно закону Ньютона-Рихмана от наружной поверхности стенки отдаётся холодной среде:

. (3.9)

Выражая из этих уравнений разности температур и складывая между собой, мы окончательно получаем выражение для плотности теплового потока q: , . (3.10)

Обозначим величину , (3.11)

К – коэффициент теплопередачи через плоскую однослойную однородную стенку. Он представляет собой количество теплоты, передаваемое в единицу времени через единицу поверхности при разности температур между средами в один градус. Значения коэффициентов теплопередачи для различных видов теплообмена будут даны в таблице в разделе конвективного теплообмена. Коэффициент теплопередачи всегда меньше меньшего α. Для того чтобы увеличить теплопередачу, нужно увеличить меньшее α. . (3.12)

Тепловой поток . (3.13)

Величина обратная коэффициенту теплопередачи – полное термическое сопротивление теплопередачи:

, (3.14)

где – термическое сопротивление теплоотдачи со стороны горячей жидкости;

– термическое сопротивление стенки (чем меньше , тем выше );

– термическое сопротивление теплоотдачи от стенки к холодной среде. .

Полное количество теплоты, передаваемое через стенку за время τ

, Дж.

Коэффициента теплопередачи не является термофизическим коэффициентом, его нет в справочниках. Он рассчитывается по формуле (3.11).Из (3.9) легко найти температуры горячей и холодной стенок:

, (3.15)

.