18. Теплоотдача при свободном движении жидкости в неограниченном пространстве

Полагаем, что объём жидкости так велик, что свободное движение, возникающее у других тел, расположенных в этом объёме, не оказывает влияния на рассматриваемое движение.

Рассмотрим случай свободной конвекции от вертикальной стенки и от горизонтальной трубы:

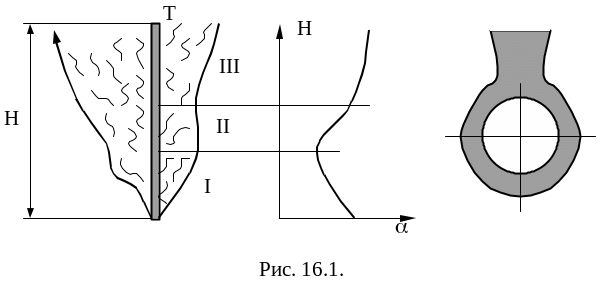
I –ламинарный режим; II–переходная зона (локонообразный режим); III –развитый турбулентный режим течения.

Для зоны I, когда :

. (16.1)

Для III зоны, когда :

. (16.2)

Для горизонтальной трубы: 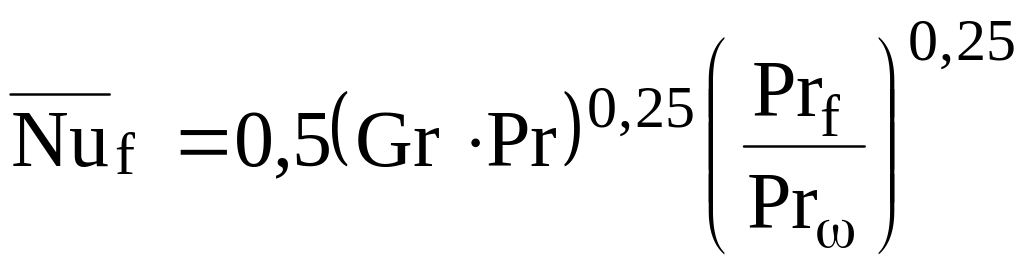. (16.3)

Эта формула справедлива для случая, когда . Характерный размер – наружный диаметр трубы.

Для очень тонких горизонтальных проволок коэффициент теплоотдачи рассчитывается по следующей формуле: .

20 Теплоотдача при свободной конвекции в ограниченном пространстве (узкие щели)

Если объём жидкости невелик, то свободное движение, возникающее у других тел или частей данного тела, расположенных в этом объёме, может оказать влияние на рассматриваемое течение жидкости при свободной конвекции.

Возьмём две вертикальных пластины и рассмотрим два случая:

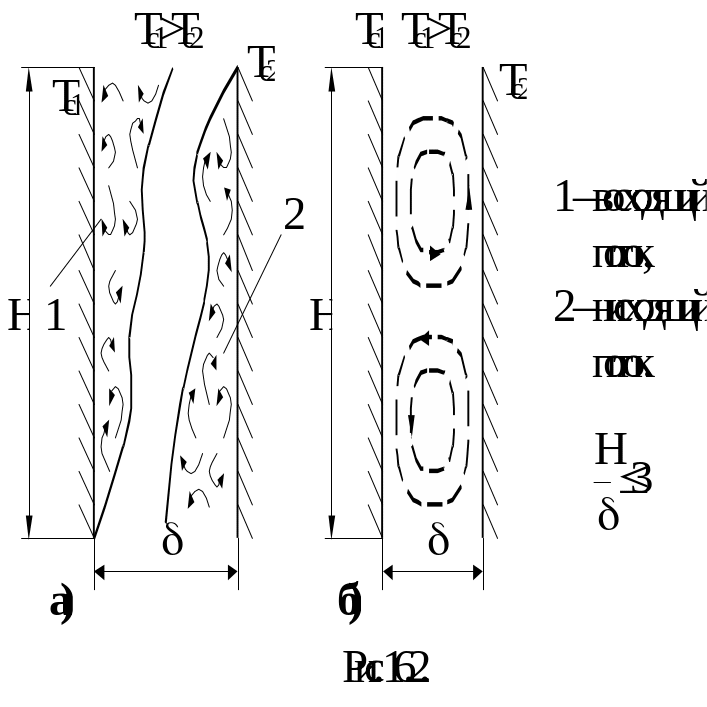
Если расстояние между пластинами  велико (рис. 16.2 (а)), то восходящие и нисходящие потоки движутся без взаимных помех. В этом случае движение и теплообмен имеют такой же характер, как и в неограниченном пространстве, и теплообмен рассчитывается по приведённым ранее (смотри вопрос 19) критериальным зависимостям (16.2).

Если расстояние между пластинами мало (рис.16.2 (б)), то вследствие взаимных помех возникают внутренние циркуляционные контуры, высота которых определяется толщиной щели . В этом случае увеличивается поток тепла от поверхности с температурой стенки Т_с1 к поверхности с температурой стенки Т_с2 за счёт конвекции. Для горизонтальной щели (рис.16.3 (а)), когда температура верхней стенки больше температуры нижней стенки щели, течение может практически отсутствовать. Если температура нижней поверхности больше температуры верхней (рис.16.3 (б)), то в щели возникают конвективные токи, чередующиеся между собой. В этом случае поток тепла от стенки с температурой Т_с1 к стенке с температурой Т_с2 возрастает за счёт конвекции.

Для практических расчётов конвективного теплообмена в ограниченном пространстве эти сложные процессы конвективного переноса теплоты через щели заменяют эквивалентным процессом теплопроводности и рассчитывают его по закону теплопроводности Фурье.

Средняя плотность теплового потока условно записывается через закон теплопроводности Фурье:

. (16.5)

В этом случае эквивалентный коэффициент теплопроводности

, (16.6)

где _к – коэффициент конвекции;

_f – коэффициент теплопроводности среды.

Если произведение , то конвекция не учитывается, и коэффициент конвекции равен 1 (чистая теплопроводность).

Если , то коэффициент конвекции рассчитывается по формуле Михеева:

. (16.7)