7. Основные характеристики соответствия данных требованиям закона нормального расп ределения (Гаусса)

Факторные показатели, учитываемые в модели, должны быть сформированы при одних и тех же или близких экономических условиях, чтобы они отвечали закону нормального распределения (закону Гаусса). Закон Гаусса: если показатель сформирован в близких экономических условиях, то вероятность появления значения показателя возрастает по мере приближения его величины к средней арифметической (иксу с черточкой сверху). Максимальная ордината (значение по вертикальной оси) рассчитывается по формуле .

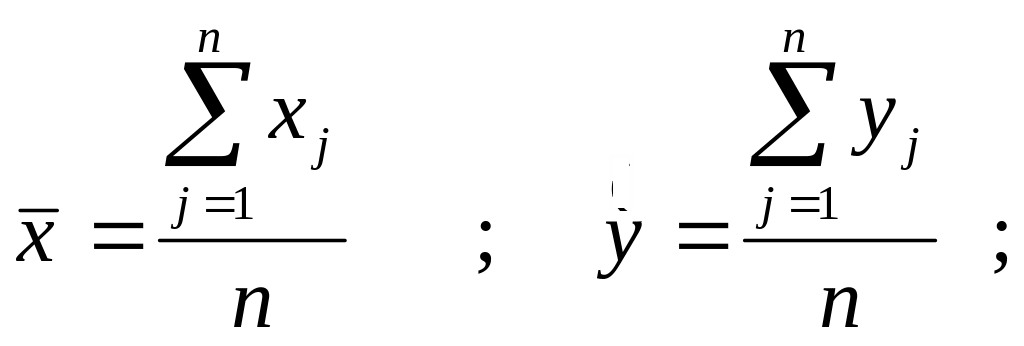
1. средние значения переменных 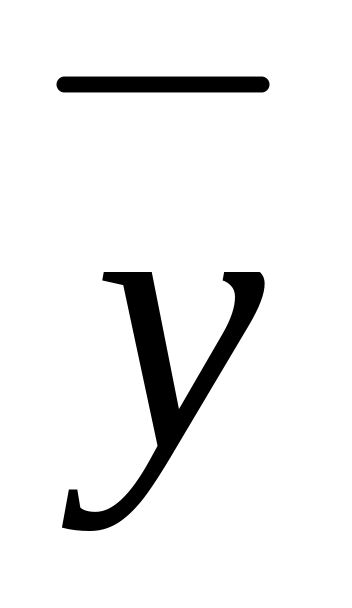- среднее значение результативного признака; _{n –число факторов}

2. отклонения от средних значений

В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии, факторов. Иными словами, имеют место отклонения фактических данных от теоретических . Величина этих отклонений и лежит в основе расчета остаточной дисперсии. Чем меньше величина остаточной дисперсии, тем меньше влияние не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным.

3. дисперсии D и средние квадратические отклонения σ:

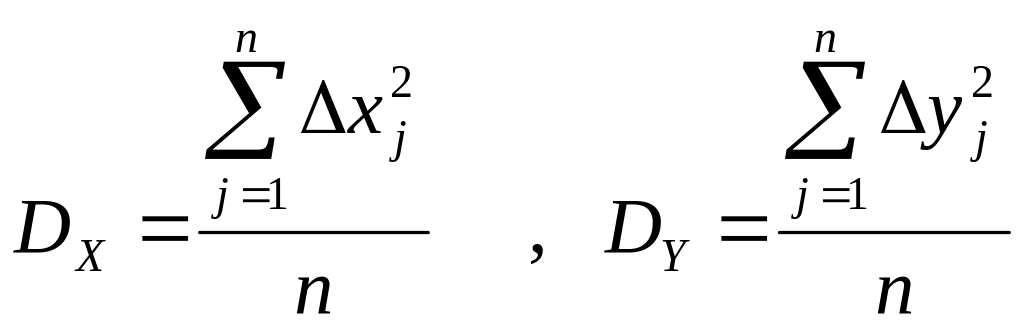
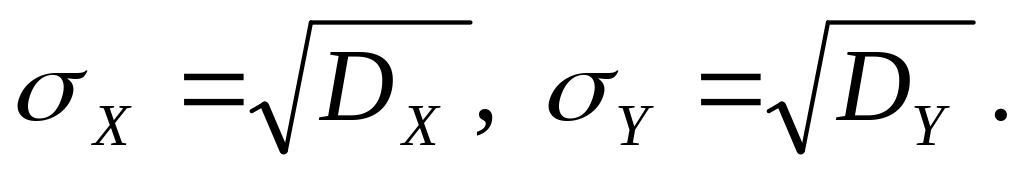
Функция нормального распределения σ² – дисперсия.

Нормальный закон распределения (закон Гаусса)– наиболее часто встречающийся на практике закон распределения. Главная особенность состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Нормальный закон, как и другие теоретические распределения, не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. А вот конкретная форма распределения задается специальными параметрами в этом уравнении. Например, всем понятно выражение типа у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Без заданных параметров невозможно четко представить эту линию. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами, которые «подгоняют» модель под реальные данные. Кривая Гаусса по форме несколько напоминает колокол, поэтому график нормального закона часто еще называют колоколообразной кривой. Если вдруг увидите термин «колоколообразная кривая», знайте, что речь идет о нормальном распределении.

Как видно, у графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Другими словами, вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

Как правило, резко выделяющиеся значения, т. е. минимумы и максимумы, вследствие проверки по закону нормального распределения приходится исключать до 25% объектов. Поэтому при сборе данных число объектов, по которым берутся данные для построения моделей, берем на 20-25% больше, чем n ≥ 20 или n ≥ 2,5k, где k – число факторов, включая результативный. Максимальные и минимальные значения, которые отбрасываются, сформированы при других экономических условиях, а не 100% являются неверными.