2.2. Критерии точности представления квантованного сигнала

В результате обратного преобразования из непрерывно-дискретной формы в непрерывную получается сигнал 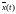, отличающийся от исходного 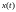на величину ошибки 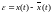. Сигнал называется воспроизводящей функцией.

Способы дискретизации и воспроизведения влияют на ошибку и ее параметры. Обычно, чем шире шаг квантования по уровню или по времени или чем меньше количество n членов разложения сигнала в ряд, тем больше ошибка и одновременно меньше данных нужно передавать через канал связи или меньше объем памяти, требуемый для хранения этого сигнала. Поэтому, зная связь между параметрами дискретизации и восстановления, надо выбирать компромиссное решение, удовлетворяющее как по точности, так и по объемам данных.

Ошибка 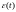является функцией времени и потому неудобна для использования в качестве критерия точности тракта дискретизация-восстановление.

Поэтому в качестве такого критерия обычно используют какой-либо функционал ошибки.

1. Чаще всего в качестве такого функционала применяют среднеквадратическую погрешность, определяемую по формуле:

.

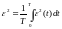Здесь Т – некоторый временной интервал, на котором находится среднеквадратическая ошибка.

2. Иногда применяют другой критерий – наибольшее отклонение:

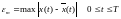
Однако его использование затруднено из-за необходимости априорного знания максимального значения сигнала и его производных.

3. Еще один критерий называется интегральным. Он находится по формуле: .

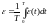Интегральный критерий характеризует в основном отклонение среднего значения воспроизведенного сигнала от исходного. Его имеет смысл использовать тогда, когда целью передачи сигнала является передача именно его среднего значения. Критерий характеризуется минимальными объемами требуемых априорных знаний о передаваемом сигнале.

Вероятностный критерий задается формулой: 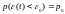, где 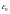− ширина доверительного интервала, а 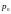− доверительная вероятность.

Вероятностный критерий показывает с какой вероятностью отклонения воспроизведенного сигнала от исходного не выйдет за пределы доверительного интервала. Очевидно, что, чем ширина интервала меньше, а вероятность выше, тем точность воспроизведения сигнала будет больше. Однако отсутствие больших отклонений от исходного сигнала при этом не гарантируется.

Информационный критерий. При использовании этого критерия рассматривается количество информации, заключенной в воспроизведенном сигнале относительно исходного.

3. Формулировка теоремы Найквиста-Котельникова и ее ограничения.

Котельников доказал, что, если некоторый сигнал x(t) имеет ограниченный сверху частотой f_m спектр, то его можно проквантовать по времени с периодом 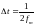и затем с абсолютной точность восстановить по формуле:

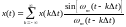(2.6)

Ряд (2.6) называется рядом Котельникова, а вышеуказанное утверждение – теоремой Котельникова.

По определению сигнал x(t) и его спектр S(jω) находятся в следующих отношениях:

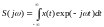; (2.7)

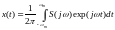. (2.8)

Формулы (2.7) и (2.8) образуют пару преобразований Фурье (прямое и обратное. Ограниченный интервал интегрирования в (2.8) – следствие ограниченности спектра, поскольку 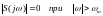. Здесь ω – круговая частота, а .

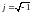Полиномы Лагранжа и их использование для восстановления непрерывных сигналов,

Воспроизводящая функция в большинстве случаев рассчитывается по формул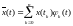е: , где 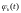− некоторые функции. Эти функции обычно стремятся выбрать так, чтобы

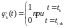. (2.14)

В этом случае 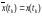, т.е. значения воспроизводящей и исходной функций совпадают в моменты взятия отсчетов или, как принято говорить, в узлах интерполяции.

Функции, обладающие этим качеством, нашел выдающийся французский математик и механик Жозеф Луи Лагранж (1736-1813).

Функции Лагранжа L зависят от одного аргумента t и двух параметров – n и k. Здесь n – максимальный номер отсчета, а k – номер функции.

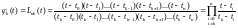(2.15)

Несложно доказать, что функции Лагранжа отвечают условию (2.14). Из формулы (2.15) следует, что функция Лагранжа является полиномом n-ой степени. Воспроизводящая функция 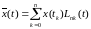по этой причине также является полиномом и называется полиномом Лагранжа n-ой степени.

Полином Лагранжа можно использовать для расчета воспроизводящей функции как при равномерной, так и при неравномерной дискретизации. Если же ограничиться только равномерной дискретизацией, полином Лагранжа можно преобразовать к виду: