2.3. Динамика поступательного движения системы материальных точек и твердого тела. Внешние и внутренние силы. Замкнутая система материальных точек. Центр масс и теорема о его движении.

Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой.

Силы взаимодействия между материальными точками механической системы называются внутренними.

Силы, с которыми на материальные точки системы действуют тела, не входящие в систему, называются внешними.

Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной).

Рассмотрим механическую систему, состоящую из n тел, массы и скорости которых соответственно равны Пусть равнодействующие внутренних сил, действующих на каждое из этих тел, а равнодействующие внешних сил.

Запишем второй закон Ньютона для каждого из n тел механической системы:

. . . . . . . . .

.

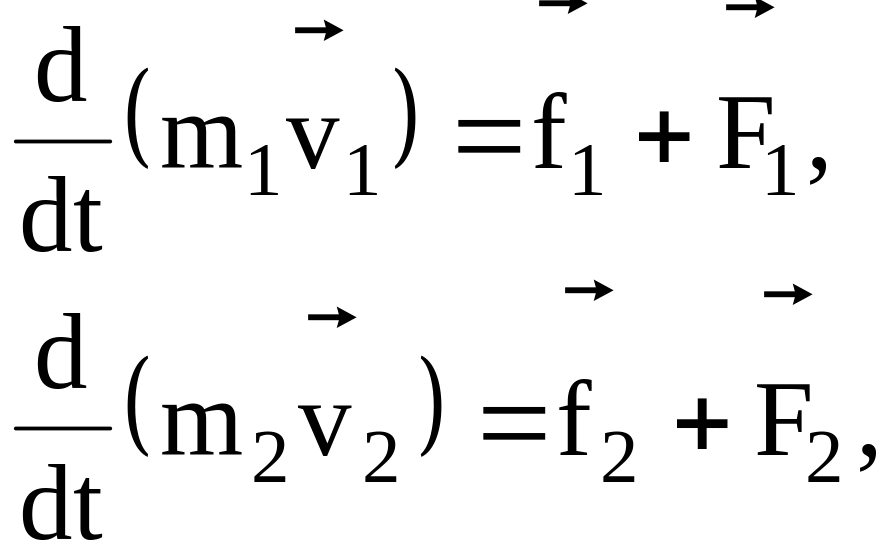
Складывая эти уравнения, получим:

Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то

,

или

, (2.3.1)

где импульс системы.

Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему. Уравнение (2.3.1) является уравнением движения механической системы.

В классической механике уравнение движения механической системы можно также записать, используя понятие центра масс системы.

Центром масс (инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение масс этой системы и радиус-вектор центра масс определяется соотношением:

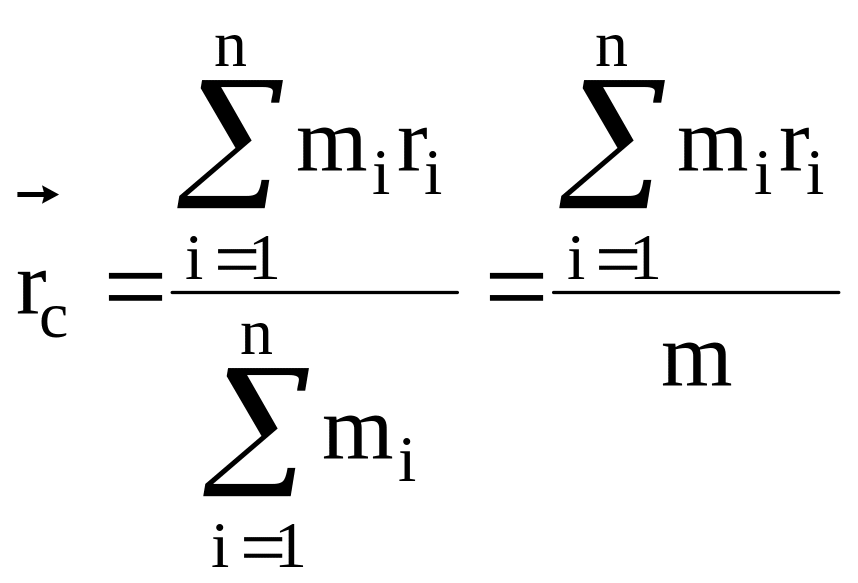, (2.3.2)

где m - масса всей системы.

Очевидно, что скорость центра масс:

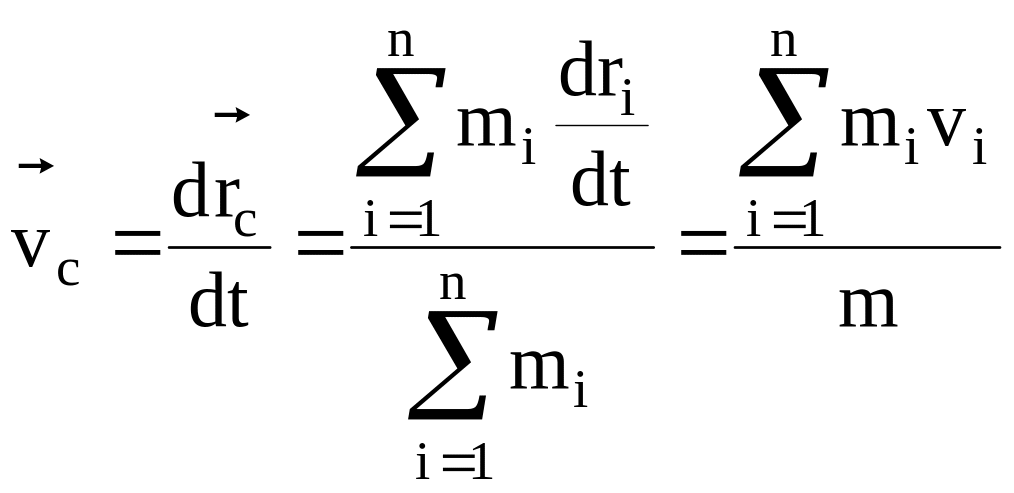. (2.3.3)

Но системы. Следовательно, получаем:

.

Учитывая выражение (2.3.1), согласно которому , получим теорему о движении центра масс:

Центр масс системы материальных точек движется как материальная точка массой, равной массе всей системы, под действием силы, равной геометрической сумме всех внешних сил, приложенных к системе.

. (2.3.4)

Из (2.3.4) очевидно, что центр масс замкнутой системы (на которую не действуют внешние силы) движется прямолинейно и равномерно или покоится.

2.4. Динамика вращательного движения. Момент инерции относительно оси вращения. Теорема Штейнера.

При изучении вращения твердого тела пользуются понятием момента инерции.

Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

. (2.4.1)

В случае непрерывного распределения масс эта сумма сводится к интегралу

, (2.4.2)

где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами x, y, z.

В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 2.1).

Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним - r+dr. Момент инерции каждого полого цилиндра (так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm - масса всего элементарного цилиндра; его объем . Если - плотность материала, то и . Тогда момент инерции сплошного цилиндра

,

но так как - объем цилиндра, то его масса , а момент инерции

.

Приведем значения моментов инерции (таблица) для некоторых тел (тела считаются однородными, m - масса тела).

Таблица

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиусом R	Ось симметрии
Сплошной цилиндр или диск радиусом R	То же
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его середину
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его конец
Шар радиусом R	Ось проходит через центр шара

Момент инерции тела является аналогом массы при вращательном движении, и также как масса является величиной – аддитивной. То есть момент инерции системы тел относительно оси равен сумме моментов инерций отдельных тел относительно данной оси.

Как видно из таблицы, момент инерции тела зависит от его размеров и формы, то есть от распределения массы, а также от положения оси вращения.

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:

Момент инерции тела J относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы m тела на квадрат расстояния (a) между осями:

.