3. Общие указания к расчету размерных цепей.

Расчет линейных и угловых размерных цепей производится методами максимума – минимума (max – min) и вероятностным.

В стандартную методику расчета включаются только номинальные размеры и допуски на них. Однако как показывает практика, отклонения от расположения поверхностей достигают до 60% общей величины исходного звена.

4. Решение обратной задачи.

4.1. Расчет сборочных размерных цепей методом максимума – минимума.

Обратная или технологическая задача заключается в определении допуска замыкающего звена при известных допусках составляющих звеньев или размеров детали.

В основе расчета размерных цепей методом максимума – минимума лежит предположение, что при сборке изделия могут сочетаться максимальные увеличивающие и минимальные уменьшающие звенья или наоборот. Таким образом, в пределы допуска замыкающего звена попадают все возможные сочетания размеров.

Решение технологической (обратной) задачи включает в себя:

1 – определение номинальной величины замыкающего звена;

2 – определение допуска на замыкающее звено;

3 – определение предельных отклонений замыкающего звена.

1) Номинальный размер замыкающего звена определяется по выражению:

(1)

где - увеличивающее звено;

- уменьшающее звено.

2. Допуск замыкающего звена определяется по формуле (1):

;

(2)

где - допуски составляющих звеньев;

3) Предельные отклонения замыкающего звена определяются через координаты середин полей допусков или по определенным отклонениям.

1. Через координаты середин полей допусков ΔC_i;

;

(3)

Предельные отклонения, es – верхнее, ei – нижнее, определяются по выражениям:

;

(4)

b) По предельным отклонениям:

;

(5)

где – соответственно верхнее, нижнее отклонения и увеличивающих звеньев;

– то же для уменьшающих звеньев.

4.2. Расчет линейных размерных цепей вероятностным методом.

Вероятность сочетаний предельных размеров деталей при сборке весьма мала. Это учитывает вероятностный метод, который позволяет получать расширенные поля допусков и тем самым уменьшить себестоимость изделия.

1. Номинальное значение замыкающего звена определяется по выражению (2):

   ;

2. Допуск замыкающего звена:

;

(6)

где:

К – коэффициент рассеивания размера (К=Т/6σ), характеризующий точность технологического процесса.

3. Координата середины поля допуска:

;

(7)

где α – коэффициент эксцентриситета, характеризующий несовпадение размера настройки и координаты середины поля допуска ΔС_i.

4. Предельные отклонения определяются по выражениям (4).

Для проектных целей, при неизвестных значениях К и α принимают:

1. для скалярных величин, которыми являются допуски размеров;

2. ; – для увеличивающих, 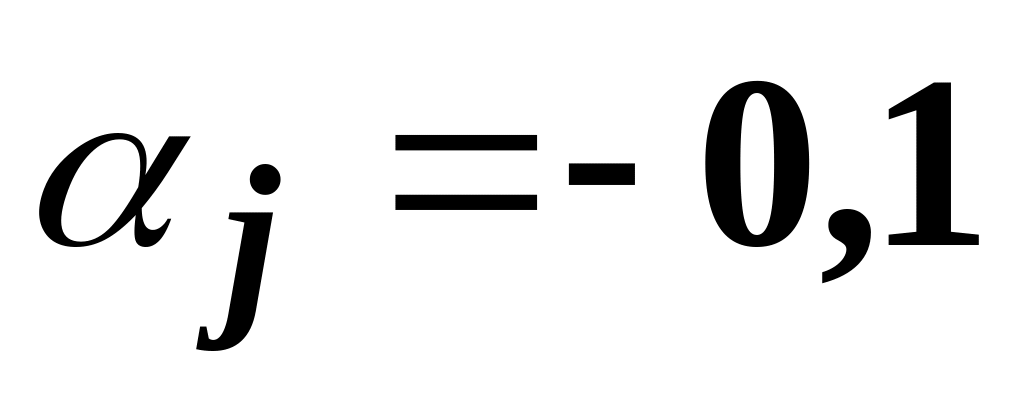– для уменьшающих звеньев.

Для проектных целей выражения (6) и (7) примут вид:

;

(6а)

;

(7а)