5Вопрос Правила нанесения размеров на чертежах

Величину детали можно определять только по размерным числам. Их наносят над размерны­ми линиями возможно ближе к их середине Размерные линии 'Ограничивают стрелками, кото­рые остриём должны касаться выносных линий , линий контура или осевых линий. Размерную линию следует проводить параллельно отрезку, размер которого указывают по возможности вне контура изображения. Расстояние между параллельными размерными линиями и от размерной линии до парал­лельной ей линии контура берут от 7 до 10 мм. Нельзя допускать, чтобы размерные линии пересе­кались с выносными или являлись продолжением линий контура, осевых, центровых и выносных. Запрещается использовать линии контура, осевые, центровые и вы­носные в качестве размерных. Чтобы размерные линии не пересекались с вынос­ными, меньший размер наносят ближе к изображению, а больший - дальше Размер стрелок следует выдерживать приблизительно одинаковым на всём чертеже. Каждый размер на чертеже указывают только один раз. Размерные числа линейных размеров наносят в со­ответствии с положением размерных линий. Если размерная линия вертикальная, то размерное число ставят справа . На наклонных размерных линиях цифры пишут так, чтобы они оказа­лись в удобном для чтения положении. Линейные размеры на машиностроительных чер­тежах указывают в миллиметрах; если размеры нанесены у изображений, то единицы измерений (мм) не простав­ляют .  Угловые размеры , их указывают в градусах (°), минутах (') и секундах ("), проставляя единицы измерения, например, размер 30°. Размерную линию при этом проводят в виде дуги окружности с центром в вершине угла.Для обозначения диаметра перед размерным чис­лом во всех случаях наносят знак - кружок, перечеркнутый прямой линией под углом 75°. Для обозначения радиуса перед размерным числом всегда наносят знак R - латинская прописная буква . Стрелку наносят с одной стороны . Если деталь имеет не­сколько   одинаковых  отвер­стий или других элементов (кроме скруглений), то нано­сится размер одного из них, а количество    отверстий или других элементов указывают перед размерным числом .Размеры толщины или длины детали, форма которой задана одним видом, наносят, как показано на рис. 10. Пе­ред числом, указывающим толщину детали, наносят бук­ву S, а перед числом, указывающим длину детали, - бук­ву L

6Вопрос. Деление отрезков, углов, окружностей на равные части.

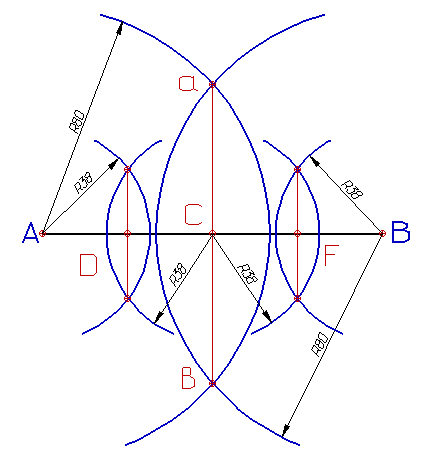
Деление отрезков:

Из концов отрезка А и В циркулем проводят две дуги окружности радиусом R, несколько большим половины отрезка, до взаимного пересечения в точках а и в.  Через полученные точки а и в проведем прямую, которая пересекает отрезок АВ в точке С, делящей отрезок на две равные части.

Проделав подобные построения для отрезков АС и СВ, получим точки D и F. Точки С, D и F делят отрезок АВ на четыре равные части.

__________________

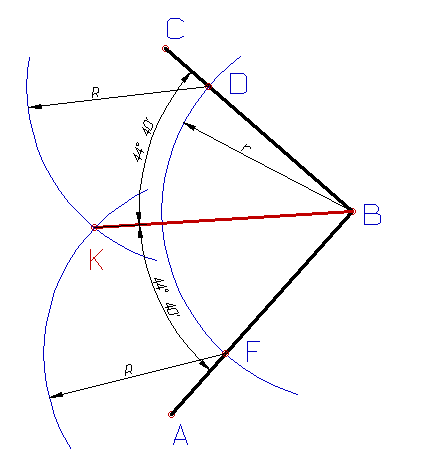
Для того чтобы разделить угол АВС пополам нужно провести биссектрису из вершины угла. Построение биссектрисы выполняется в следующей последовательности:

• Из вершины угла проводят дугу окружности произвольного радиуса r до пересечения со сторонами угла в точках D и F;

• Из полученных точек проводят две дуги радиусом R, величина которого больше половины длины дуги DF, до взаимного пересечения в точке К;

Прямая проходящая через вершину В и точку К - биссектриса данного угла т.е. делит угол на две равные части.

_________________

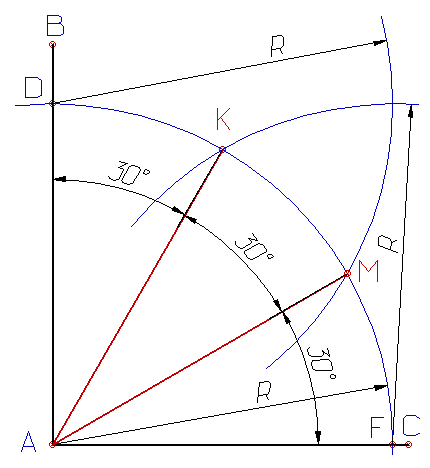
Деление прямого угла на три равные части

Деление прямого угла АВС на три равные части выполняется в следующей последовательности: Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F; Из полученных точек проводят две дуги тем же радиусом R,  до взаимного пересечения пересечения с дугой DF в точках К и М; Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.

_____________________

Деление окружности на восемь равных частей. Чтобы разделить окружность на восемь равных частей, достаточно провести две пары диаметров, т. е. объединить оба случая построения квадрата. Одну пару взаимно перпендикулярных диаметров строят по катетам, другую — по гипотенузе угольника. ___________________ Деление окружности на три равные части. Поставив опорную ножку циркуля в конец диаметра, описывают дугу радиусом, равным радиусу R окружности. Получают первое и второе деления. Третье деление находится на противоположном конце диаметра. Ту же задачу можно решить с помощью линейки и угольника с углами 30 и 60°. Для этого устанавливают угольник большим катетом параллельно вертикальному диаметру. Вдоль гипотенузы из точки 1 (первое деление) проводят хорду; получают второе деление . Перевернув угольник и проведя вторую хорду, получают третье деление. Соединив точки 2 и 3 прямой, получают равносторонний треугольник. ___________________ Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности. Из противоположных концов одного из диаметров окружности(точек 1,4) описывают дуги. Точки 1, 2, 3, 4, 5, 6 делят окружность на равные части. Соединив их прямыми, получают правильный шестиугольник. Ту же задачу можно выполнить при помощи линейки и угольника с углами 30 и 60°. Деление окружности на пять равных частей. Пятой части окружности соответствует центральный угол в 72° (360°: 5 = = 72°). Этот угол можно по строить при помощи транспортира. Дальнейшее деление окружности выполняют при помощи хорды найденной дуги. Соединив точки хордами, получим правильный вписанный пятиугольник. Показано вычерчивание пятиконечной звезды, основанное на делении окружности. на пять равных частей.