П.3 Обратная матрица
Матрица B называется обратной к матрице
,
если справедливо равенство:
.
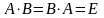Обозначение:
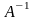
− Только квадратная матрица может иметь обратную матрицу.
− Не всякая квадратная матрица имеет обратную матрицу.
Свойства:
;
;
,
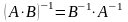где матрицы
−квадратные,
одинаковой размерности.
Квадратная матрица называется невырожденной, если её определитель не равен нулю. В противном случае матрица называется вырожденной.
Матрицей, союзной к матрице А, называется транспонированная матрица алгебраических дополнений элементов аij данной матрицы:
.
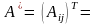
Теорема.
Всякая невырожденная матрица имеет
обратную, при этом
.
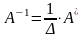►Проведем
доказательство для случая матрицы 3-го
порядка. Пусть
.
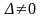Составим союзную матрицу А*=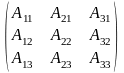
и найдем произведение:
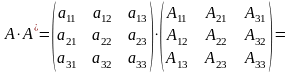
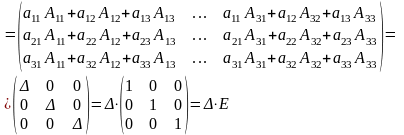
Умножая слева обе части равенства на матрицу , получим:
.
■
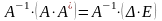
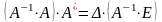
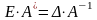
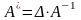
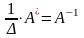Пример
Для нахождения обратной матрицы можно использовать метод элементарных преобразований строк:
Составляют расширенную матрицу, приписывая справа от исходной матрицы единичную матрицу соответствующей размерности:
.
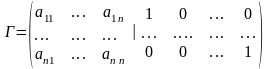Элементарными преобразованиями строк матрицу Г приводят к виду:
.
−
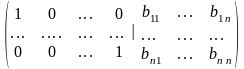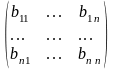искомая обратная матрица
.
П.12 Ранг матрицы
Минором k-ого порядка матрицы
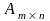называется определитель, составленный
из элементов исходной матрицы, стоящих
на пересечении любых k
строк и k столбцов
(
).
Замечание. Каждый элемент матрицы является ее минором 1-го порядка.
Теорема. Если в матрице все миноры k-ого порядка равны нулю, то равны нулю все миноры большего порядка.
►Разложим минор (определитель) (k+1)-ого
порядка через элементы 1-ой строки:
.
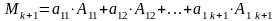Алгебраические
дополнения по сути являются минорами
k-ого порядка,
которые по условию теоремы равны нулю.
Следовательно,
.
■
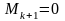В матрице порядка
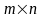минор порядка
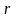называется базисным, если
он не равен нулю, а все миноры порядка
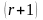и выше равны нулю, или не существуют
вовсе, т.е.
совпадает с меньшим из чисел
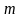или
.
Столбцы и строки матрицы, из которых стоит базисный минор, называются базисными.
В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Порядок базисного минора матрицы называется рангом матрицы и обозначается:
,
.
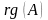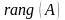Очевидно,
что
.
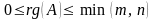Например.
1.
,
.
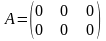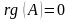2.
.
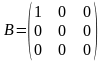Матрица
В содержит единственный ненулевой
элемент
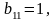являющийся минором 1-го порядка. Все
определители более высоких порядков
будут содержать 0-ю строку и поэтому
равны 0. Следовательно,
.
Свойства:
При транспонировании матрицы ее ранг не меняется:
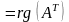;Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится;
Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Ранг ступенчатой матрицы
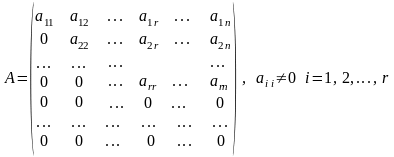
равен числу её ненулевых строк.
Примеры: Определить ранг матрицы.
1.
.
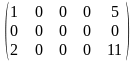
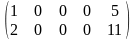
2.
.
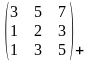
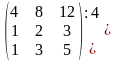
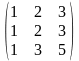
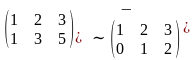П.5 Системы линейных уравнений (слу)
Линейным называется уравнение, содержащее переменные только в первой степени и не имеющее произведения переменных.
Совокупность линейных уравнений называют СЛУ:
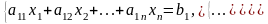
Если все свободные числа
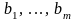равны нулю, то СЛУ называется
однородной (СЛОУ).Если существует хотя бы одно свободное число
,
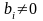то СЛУ называется неоднородной
(СЛНУ).Решением СЛУ называется такой набор чисел
,
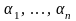который при подстановке в систему
вместо неизвестных преобразует уравнения
в верные числовые равенства.СЛУ называется совместной, если она имеет хотя бы одно решение.
Совместная система называется определенной, если она имеет единственное решение; и неопределенной, если она имеет более одного решения.
В последнем случае каждое её решение называется частным решением СЛУ. Совокупность всех частных решений называется общим решением.