§1. Линейная алгебра п.1 Матрица. Основные понятия

Таблицу чисел, содержащую строк и столбцов, называют матрицей размера :

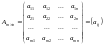, где и .

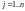Место каждого элемента 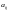однозначно определяется номером i−строки и j−столбца, на пересечении которых он находится.

• Матрицы 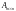и 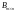равны между собой 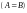, если равны все соответствующие элементы этих матриц: .

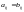• Матрицы и называются эквивалентными 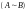, если одна из них получается из другой с помощью элементарных преобразований:

1. Перестановка местами двух строк (двух столбцов).

2. Умножение (деление) всех элементов строки (столбца) матрицы на число отличное от нуля.

3. Прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и тоже число.

Виды матриц:

• Матрица, содержащая один столбец (одну строку), называется столбцовой (строчной) матрицей или вектором (вектор-столбец или вектор-строка соответственно).

• Матрица, все элементы которой равны нулю, называется нулевой .

• Если число столбцов матрицы равно числу строк , то матрица называется квадратной .

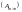− Элементы квадратной матрицы, стоящие на диагонали, идущей из верхнего левого угла, образуют главную диагональ: .

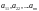− Элементы квадратной матрицы, стоящие на диагонали, идущей из верхнего правого угла, образуют побочную диагональ: .

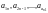• Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной: .

• Диагональная матрица, у которой каждый элемент главной диагонали равен единице называется единичной матрицей: .

В матричном исчислении нулевая 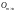и единичная 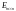матрицы играют роль чисел 0 и 1.

• Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной (побочной) диагонали, равны нулю.

• Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной.

Если матрица 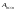, то .

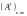Транспонированная матрица обладает следующим свойством: .

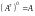• Матрица, у которой равны элементы, симметричные относительно главной диагонали, называется симметрической.

П.2 Основные действия над матрицами

1. Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Единственным условием этих операций является то, что они определены только для матриц одинакового размера.
	, ; .	1. ; 2. ; 3. ; 4. ; 5. .

Пример:

2. Умножение матрицы на число сводится к соответствующей операции над её элементами.
	, ; .	1. ; 2. ; 3. ; 4. .

Пример:

• Противоположной матрицей 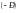для исходной матрицы называется матрица, у которой все элементы имеют противоположный знак по отношению к соответствующим элементам исходной матрицы: .

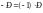  3. Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
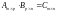
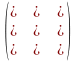
  	, ; . «строчка на столбец»: элемент i−строки и j−столбца матрицы С равен сумме произведений элементов i−строки матрицы А на соответствующие элементы j−столбца матрицы В.	1. 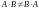; 2. ; 3. 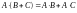; 4. 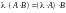; 5. .

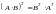• Если для матриц выполняется коммутативный закон умножения 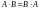, то матрицы называются перестановочными.

Перестановочными могут быть только квадратные матрицы одного и того же порядка.

Единичная матрица является перестановочной с любой другой матрицей того же размера: .

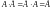Нулевая матрица является перестановочной с любой другой матрицей того же размера: .

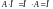4. Возведение матрицы в степень возможно только для квадратной матрицы.
	; ; ; .

Примеры.

1. Найти произведения матриц 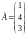и .

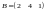Решение:  = .

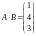
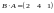
 = (21 + 44 + 13) = (21).

2. Даны матрицы 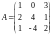, , 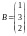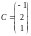. Найти .

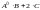Решение: ; ;

 = = ;

+ = .
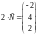
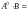
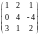
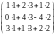
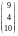
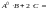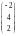
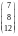
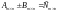
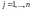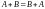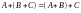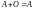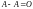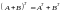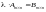
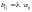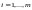
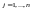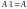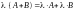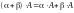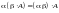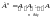
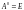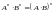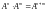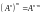