Пример проектирования лексического анализатора
Пусть {Li
| Li
A*
, i
[1,3]} –
семейство из трех регулярных языков
над входным алфавитом A,
где Li
– класс лексем языка Си или его ограничение
(подмножество)
для всех
i
[1, 3].
Язык L1 – множество идентификаторов языка Си; L2 - множество целочисленных констант языка Си в системе счисления с основанием 8; L3 – множество «пробельных» лексем, интерпретируемых как непустые слова над алфавитом {s, t}. Символы s и t условно обозначают «пробел» и «знак табуляции» соответственно.
Входной алфавит A представляют 256 символов в 8 – разрядной (байтовой) ASCII-кодировке. Числовой код символа «пробел» 0x20 и «знака табуляции» 0x09.
Языки Li индуцируют разбиения i алфавита A, i [1,3]: 1 = {[_a-zA-Z], [0-9], [^_a-zA-Z]}; 2 = {[0], [1-7], [lL], [uU], [^01-7 lL uU]}, 3 = {[\x20\x09], [^\x20\x09]}. Абстрактные алфавиты, соответствующие разбиениям, следующие: B1 = {a, 9, ? }, B2 = {0, 7, l, u, ? }, B3 = {s, ? }, Регулярные выражения еi представляют языки Li в соответствующих абстрактных алфавитах Bi , i [1,3] : e1 = а(а | 9)*, e2 = 0(0 | 7)* (λ|u|l|ul|lu), e3 = ss *.
Эквивалентные λ-диаграммы Di для еi , i [1,3] :
e1 = а (а | 9)*;
а:
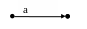
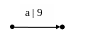
(а | 9):
(
а
| 9)*:
e1 = а (а | 9)*:
λ-диаграммa D1
а
λ
λ
а|9
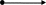
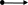
e2 = 0(0 | 7)* (λ|u|l|ul|lu):
λ-диаграммa D2
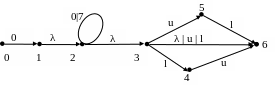
e3 = s s*:
λ-диаграммa D3
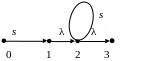
Детерминированные конечные автоматы Mi, допускающие языки l(Di), I [1,3]. Символом ‘*’ помечены финальные состояния, символом состояние “ошибки”. M1
Замыкание |
q\a |
a |
9 |
? |
[0]= {0} |
0 |
1 |
|
|
[1]={1, 2, 3} * |
1 |
3 |
3 |
|
[]= |
2 |
|
|
|
[{2,3}]={2,3} * |
3 |
3 |
3 |
|
M2
Замыкание |
q\a |
0 |
7 |
l |
u |
? |
[0]= {0} |
0 |
1 |
|
|
|
|
[1]={1,2,3,6} * |
1 |
3 |
3 |
4 |
5 |
|
[] = |
2 |
|
|
|
|
|
[2]={2,3, 6} * |
3 |
3 |
3 |
4 |
5 |
|
[{4,6}]={4,6} * |
4 |
|
|
|
6 |
|
[{5,6}]={5,6} * |
5 |
|
|
5 |
|
|
[6]= {6} * |
6 |
|
|
|
|
|
M3
Замыкание |
q\a |
s |
? |
[0]= 0 |
0 |
1 |
2 |
[1]={1, 2, 3} * |
1 |
3 |
|
[] = |
2 |
|
|
[{2,3}]={2,3} * |
3 |
3 |
|
Языки Li – не пусты, поскольку не пусты множества заключительных состояний автоматов Mi для всех i [1,3] , и λ-свободны, так как начальные состояния не являются заключительными;
Общий алфавит B = {0, 7, 9, a, l, u, s, ?}. Соответствующее разбиение алфавита A = {[0], [1-7], [89], [_a-km-tv-zA-KM-TV-Z], [lL], [uU], [\x20\x09], [^0-9_a-zA-Z\x20\x09]}.
Элементы алфавитов связаны следующими соотношениями:
элементы B1 = {a, 9, ?} – a = а | l | u,
9 = 0 | 7 | 9,
? = s | ?;
элементы B2 = {0, 7, l, u, ?} – 0 = 0,
7 = 7,
l = l,
u = u,
? = 9 | a | s | ?;
элементы B3 = {s, ?} –
s = s, t = t, ? = 0 | 7 | 9 | а | l | u | ?.
Применяя соотношения как правила подстановки к исходным выражениям, получаем регулярные выражения над общим алфавитом B:
e1 = (а | l | u)(а | l | u | 0 | 7 | 9)* ,
e2 = 0(0 | 7)* (λ|u|l|ul|lu),
e3 = ss*. Чтобы получить регулярные выражения, определяющие языки в исходном алфавите A, необходимо заменить вхождения символов алфавита B в регулярные выражения на выражения, представляющие соответствующие классы разбиения . Например, в языке C# выражения имеют следующие представления в формате строковых констант (литералов): e1 @”([_a-km-tv-zA-KM-TV-Z] | [lL] | [uU])”+ @”( [_a-km-tv-zA-KM-TV-Z] | [lL] | [uU] | [0] | [1-7] | [89])*” ; e2 @”[0]([0] | [1-7])* ( [uU] | [lL] | [uU] [lL] | [lL] [uU])?”;
e3 @” [\x20\x09] [\x20\x09]*”.
Диаграммы Di в алфавитах Bi также просто преобразуются в соответствующие диаграммы над общим алфавитом B: достаточно каждую a-дугу заменить параллельными b-дугами. Например, в диаграмме D1 каждая дуга (i, a, j) заменяется на (i, а | l | u, j), дуга (i, 9, j) – на (i, 0 | 7 | 9, j) и (i, ?, j) – на (i, s | t |?, j).
Приведенные к общему алфавиту B λ-диаграммы Di, i [1,3]:
e1 = (а | l | u)(а| l | u | 0 | 7 | 9)* ;
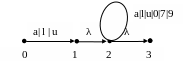
e2 = 0(0 | 7)* (λ|u|l|ul|lu):
λ-диаграммa D2
e3 = ss* :
λ-диаграммa D3
Детерминированные конечные автоматы Mi , приведенные к общему алфавиту B, i [1,3] . M1
Замыкание |
q\a |
0 |
7 |
9 |
a |
l |
u |
s |
? |
[0]= {0} |
0 |
|
|
|
1 |
1 |
1 |
|
|
[1]={1, 2, 3 } * |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
[] = |
2 |
|
|
|
|
|
|
|
|
[{2,3}]={2,3} * |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
M2
Замыкание |
q\a |
0 |
7 |
9 |
a |
l |
u |
s |
? |
[0]= {0} |
0 |
1 |
|
|
|
|
|
|
|
[1]={1,2,3,6} * |
1 |
3 |
3 |
|
|
4 |
5 |
|
|
[] = |
2 |
|
|
|
|
|
|
|
|
[2]={2,3,6} * |
3 |
3 |
3 |
|
|
4 |
5 |
|
|
[{4,6}]= {4,6} * |
4 |
|
|
|
|
|
6 |
|
|
[{5,6}]= {5,6} * |
5 |
|
|
|
|
6 |
|
|
|
[6]= {6} * |
6 |
|
|
|
|
|
|
|
|
M3
Замыкание |
q\a |
0 |
7 |
9 |
a |
l |
u |
s |
? |
[0]= 0 |
0 |
|
|
|
|
|
|
1 |
|
[1]={1, 2, 3} * |
1 |
|
|
|
|
|
|
3 |
|
[] = |
2 |
|
|
|
|
|
|
|
|
[{2,3}]={2,3} * |
3 |
|
|
|
|
|
|
3 |
|
Языки Li над общим алфавитом B так же не пусты, поскольку не пусты множества заключительных состояний автоматов Mi для всех i [1,3] , и λ-свободны, так как начальные состояния не являются заключительными.
Декартово
произведение двух детерминированных
конечных автоматов
aвтомат M1,2= M1
x M2 ,
допускающий объединение исходных
языков: L1
L2 .
M1,2
Вектор |
q\a |
0 |
7 |
9 |
a |
l |
u |
s |
? |
(0,0) |
0 |
1 |
|
|
3 |
3 |
3 |
|
|
(2,1) 2 |
1 |
4 |
4 |
|
|
5 |
6 |
|
|
(2,2)= |
2 |
|
|
|
|
|
|
|
|
(1,2) 1 |
3 |
7 |
7 |
7 |
7 |
7 |
7 |
|
|
(2,3) 2 |
4 |
4 |
4 |
|
|
5 |
6 |
|
|
(2,4) 2 |
5 |
|
|
|
|
|
8 |
|
|
(2,5) 2 |
6 |
|
|
|
|
8 |
|
|
|
(3,2) 1 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
|
|
(2,6) 2 |
8 |
|
|
|
|
|
|
|
|
Декартово произведение трех детерминированных конечных автоматов aвтомат M= M1 x M2 x M3 , допускающий объединение исходных языков: L1 L2 L3. M
Вектор |
q\a |
0 |
7 |
9 |
a |
l |
u |
s |
? |
(0,0,0) |
0 |
1 |
|
|
3 |
3 |
3 |
4 |
|
(2,1,2) 2 |
1 |
5 |
5 |
|
|
6 |
7 |
|
|
(2,2,2)= |
2 |
|
|
|
|
|
|
|
|
(1,2,2) 1 |
3 |
8 |
8 |
8 |
8 |
8 |
8 |
|
|
(2,2,1) 3 |
4 |
|
|
|
|
|
|
9 |
|
(2,3,2) 2 |
5 |
5 |
5 |
|
|
6 |
7 |
|
|
(2,4,2) 2 |
6 |
|
|
|
|
|
10 |
|
|
(2,5,2) 2 |
7 |
|
|
|
|
10 |
|
|
|
(3,2,2) 1 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
|
|
(2,2,3) 3 |
9 |
|
|
|
|
|
|
9 |
|
(2,6,2) 2 |
10 |
|
|
|
|
|
|
|
|
Пусть M =(Q, B , g, q0, F), где F= F1 F2 F3 , F1 = {3, 8}, F2 = {1, 5, 6, 7, 10}, F3 = {4, 8}. Соответствующие автоматы (Q, B , g, q0, Fi) допускают языки Li , i [1,3] .
Cемейство подмножеств {F1, F2, F3} состоит из попарно не пересекающихся множеств, следовательно семейство языков {L1, L2, L3} состоит из трех попарно не пересекающихся регулярных языков;
Автомат M , построенный методом «слияния диаграмм переходов» автоматов M1,2 и M3. Автоматы M и M изоморфны, поскольку их диаграммы переходов изоморфны. M
F |
q\a |
0 |
7 |
9 |
a |
l |
u |
s |
? |
|
0 |
1 |
|
|
3 |
3 |
3 |
9 |
|
2 |
1 |
4 |
4 |
|
|
5 |
6 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
3 |
7 |
7 |
7 |
7 |
7 |
7 |
|
|
2 |
4 |
4 |
4 |
|
|
5 |
6 |
|
|
2 |
5 |
|
|
|
|
|
8 |
|
|
2 |
6 |
|
|
|
|
8 |
|
|
|
1 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
|
|
2 |
8 |
|
|
|
|
|
|
|
|
3 |
9 |
|
|
|
|
|
|
10 |
|
3 |
10 |
|
|
|
|
|
|
10 |
|
Классификация состояний и переходов. По построению все состояния достижимы из начального состояния q0.
Множество «тупиковых» или состояний, сигнализирующих о лексической ошибке, Error ={q| g*(q, x) F}.
В автомате M= M1 x M2 x M3 множество Error = {2}, так как из q2 не достижимо ни одно финальное состояние q F.
Множество активных состояний Active = Q\ Error. Множество активных переходов ActiveTransition = {(q, a)| q Active и g(q, a) Active, a B }. Множество переходов, определяющих условие распознавания лексемы класса Li , EndLi = {(q, a)| q Fi и g(q, a) Error, a B }.
Символ a такой, что (q, a) EndLi определяет правый контекст лексемы x Li. Слово x переводит автомат из начального состояния в финальное состояние qFi, причем q =g*(q0, x).
Переходы множества ErrorL = {(q, a)| q Active \ F и g(q, a) Error, a B } определяют условия обнаружения лексической ошибки. Если (q, a) ErrorL, тогда слово x такое, что q =g*(q0, x) переводит автомат из начального состояния в активное не финальное состояние q, определяет допустимый собственный префикс некоторой лексемы, но
слово xa – не допустимый префикс, так как не существует слова y B*, что xaу L.
Очевидно, ActiveTransition, EndL1 , EndL2 , EndL3 , ErrorL, попарно не пересекающиеся множества переходов.
Семантические процедуры
Определить (классифицировать) множество P «действий» (семантических процедур) значит определить функцию выхода f : QB → P, где B= B {#}. Если f(q,a)=p P, тогда p – действие, выполняемое лексическим анализатором в состоянии q Q при входном символе a B. Формально символ # B служит признаком конца входного потока. Фактически результатом проектирования является разработка модели детерминированного конечного преобразователя M = (Q, B, P, f, g) простого типа.
Пусть P = { pActiveTransition, pEndL1, … , pEndLn, pErrorL}. Определим очевидным образом функцию выхода:
f(q,a)=pActiveTransition, если (q,a)ActiveTransition;
если (q,a) EndLi , то (q,#) EndLi , и f(q,a)=pEndLi, если (q,a) EndLi , i [1, n];
если (q,a) ErrorL, то (q,#) ErrorL, и
f(q,a)=pErrorL, если (q,a) ErrorL.
Тогда программная реализация (интерпретация) преобразователя M = (Q, B, P, f, g) определяет основные действия (функции) лексического анализатора при сканировании входного потока символов алфавита B.
Ниже на псевдоязыке приводится в обобщенной форме одна из возможных программных интерпретаций.
Интерпретация символов выходного алфавита P.
pActiveTransition:
s = s + a; //добавить входной символ, расширить префикс некоторой //лексемы
// q1 = <q>
q = g[q,b]; // b = [a] – класс входного символа а #
// q2 = <q> и (q1, b, q2) in ActiveTransition`
return;
pEndLi , i [1, n]:
//(q, b) in EndLi , i [1, n]
//<s> = x – лексема, b = [a] и <a> = a – правый контекст
tokenStream.WriteLine(“<L”, i, “>”, s);
if (b == [#])
{
//выход
return;
}
else
{
inputStream.UnGetC(a); // вернуть символ <a> = a во входной поток q = 0; // переключить автомат в начальное состояние
s=””; // очистить буфер для накопления символов очередной лексемы
return;
}
pErrorL:
s = s + a;
tokenStream.WriteLine(“<ErrorL>”, s); //s=xa
if (b == [#])
{
//выход
return;
}
else
{
//skip входной символ а, доставивший лексическую ошибку q = 0;
s=””;
return;
}