6.6. Кривые второго порядка. Окружность

Пусть на плоскости задана прямоугольная система координат 0ху.

Кривой второго порядка называется линия на плоскости, определяемая уравнением второй степени относительно текущих координат точки М(х, у, z). В общем случае это уравнение имеет вид:

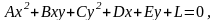
где коэффициенты А, В, С, D, E, L – любые действительные числа, причем хотя бы одно из чисел А, B, С отлично от нуля.

Далее рассмотрим четыре вида кривых второго порядка: окружность, эллипс, гипербола и парабола.

1.Окружностью называется множество точек на плоскости, расстояние от которых до фиксированной точки М₀(х₀, у₀) постоянно и равно R. Точка М₀ называется центром окружности, а число R – ее радиусом

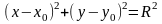
– уравнение окружности с центром в точке М₀(х₀, у₀) и радиусом R.

Если центр окружности совпадает с началом координат, то имеем:

– каноническое уравнение окружности.

2. Эллипс.

Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух данных точек есть величина постоянная (причем эта величина больше расстояний между данными точками). Данные точки называются фокусами эллипса.

– каноническое уравнение эллипса.

Отношение называется эксцентриситетом эллипса и обозначается: , 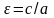. Так как 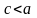, то < 1.

Следовательно, с уменьшением отношение стремится к 1, т.е. b мало отличается от а и форма эллипса становится ближе к форме окружности. В предельном случае при , получается окружность, уравнение которой есть

х² + у² = а² .

4. Гипербола

Гиперболой называется множество точек на плоскости, для каждой из которых абсолютная величина разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная (при условии, что эта величина меньше расстояния между фокусами и не равна 0).

Пусть F₁, F₂ – фокусы, расстояние между ними обозначим через 2с,

– каноническое уравнение гиперболы.

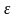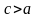Отношение называется эксцентриситетом гиперболы и обозначается , т.е. . Так как , то . Из формулы имеем: ,

Следовательно, эксцентриситет характеризует форму гиперболы.

4. Парабола

Параболой называется множество точек на плоскости, для каждой из которых расстояние до данной точки (называемой фокусом) равно расстоянию до данной прямой (называемой директрисой).

Пусть F – фокус, l – директриса параболы, р – расстояние от фокуса F до директрисы l (назовем р параметром параболы).

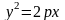
– каноническое уравнение параболы.

Заметим, что уравнение 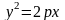при отрицательном р также задает параболу, которая будет расположена слева от оси 0у . Уравнение описывает параболу, симметричную относительно оси 0у, лежащую выше оси 0х при р > 0 и лежащую ниже оси 0х при р < 0.

П.6.7. Поверхности второго порядка.

Пусть в пространстве задана прямоугольная декартова система координат 0xyz. Поверхность называется поверхностью второго порядка, если она задается уравнением второй степени относительно текущих координат х, у, z.

1.Сферой называется множество точек в пространстве, удаленных от данной точки (называемой центром) на одно и то же расстояние (называемое радиусом).

– уравнение сферы с центром в точке S(a, b, c) и радиусом R. Если центр совпадает с началом координат 0(0, 0, 0), то получаем

– каноническое уравнение сферы.