
- •Мфюа. Маси. Кафедра оменд 2015
- •Математика часть 1. Линейная алгебра. Лекция 1.
- •Тема 1. Векторная алгебра.
- •П.1. Системы координат на плоскости и в пространстве.
- •П.2. Векторы.
- •П.2.2. Координаты вектора. Координатная запись вектора. П.3. Скалярное произведение векторов и его свойства.
- •Вычисление угла между векторами Из определения скалярного произведения и формул (2.5), (2.9) следует, что
- •Условие перпендикулярности векторов
- •П.4. Векторное произведение векторов и его свойства.
- •Свойства векторного произведения векторов
- •П.5. Смешанное произведение векторов и его свойства.
- •Вычисление объема тетраэдра и параллелепипеда, построенного на векторах (рис. 2.10).
- •Вычисление высоты тетраэдра (параллелепипеда).
- •Условие компланарности векторов (теорема 2.1):
- •Задание на Дом:
- •Тема 1. Векторная алгебра.
- •Тема 2. Матрицы и определители. П.2.1. Понятие матрицы
- •1.5. Действия над матрицами
- •П.2.2. Определители.
- •Разложение определителя по строке или столбцу
- •Тема 6. Аналитическая геометрия.
- •1.Уравнение прямой по угловому коэффициенту и точке:
- •3.Уравнение прямой по точке и направляющему вектору:
- •4.Уравнение прямой по двум точкам.
- •Уравнение прямой в отрезках имеет вид , где – ненулевые константы.
- •И, наконец, последний нами рассматриваемый тип уравнения прямой:
- •7.Уравнение прямой в параметрической форме:
- •П.6.2. Взаимное расположение двух прямых
- •6.6. Кривые второго порядка. Окружность
- •2. Эллипс.
- •4. Гипербола
- •4. Парабола
- •П.6.7. Поверхности второго порядка.
- •2. Эллипсоиды.
- •3.Цилиндрические поверхности.
- •4. Конические поверхности.
- •5. Гиперболоиды.
- •6.Параболоиды.
- •Литература.
- •Данко п.Е. И др. Высшая математика в упражнениях и задачах: в 2-х томах. – м.: Высшая школа, 2010.
- •Письменный д.Т. Конспект лекций по высшей математике: – м.: Айрис-пресс, 2007. -608 с.: ил. –(Высшее образование), isbn 5-8112-2893-7, 978-5-8112-2893-5.
- •Математика для заочников http://www.Mathprofi.Ru
Вычисление объема тетраэдра и параллелепипеда, построенного на векторах (рис. 2.10).
Если векторы некомпланарны, то по теореме 2.1
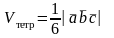 -
объем тэтраэдра. (2.13)
-
объем тэтраэдра. (2.13)
 объем
параллепипеда.
объем
параллепипеда.
Вычисление высоты тетраэдра (параллелепипеда).
Вычислим объем тетраэдра двумя способами:
с одной стороны,
 ,
,
с другой стороны,

отсюда
 (высота параллелепипеда такая же);
(высота параллелепипеда такая же);
Условие компланарности векторов (теорема 2.1):
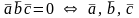 – компланарны.
– компланарны.
Задание на Дом:
РЕШИТЬ ЗАДАЧИ
Тема 1. Векторная алгебра.
1.Даны
векторы
2.Даны
векторы
Найти
скалярное произведение
3.Даны
векторы
(1;1)
и
(-5;2).
Найти скалярное произведение
|
4.Определить
площадь треугольника, построенного
на векторах
|
5.Определить площадь треугольника, построенного на векторах =(1;2;0), =(2;-1;3). |
6.Определить
объём параллелепипеда, построенного
на векторах
=(-1;1;0),
=(3;1;1),
|
Тема 2. Матрицы и определители. П.2.1. Понятие матрицы
Опр. 1. Прямоугольная таблица чисел, состоящая из m строк и n столбцов, называется матрицей.
Для обозначения матриц используются прописные буквы латинского алфавита: А, В, С, ....
Числа,
образующие матрицу, называются ее
элементами. В обозначениях элементы
матрицы, снабжаются двумя индексами i,
j, первый индекс – номер строки, второй
индекс – номер столбца, в которых
находится элемент, т.е.
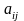 (i = 1, 2, ..., m; j = 1, 2, ..., n) элементы матрицы.
Таким образом, полное обозначение
матрицы имеет вид:
(i = 1, 2, ..., m; j = 1, 2, ..., n) элементы матрицы.
Таким образом, полное обозначение
матрицы имеет вид:
 .
(2.1)
.
(2.1)
Для краткого обозначения матрицы будем использовать запись:
 (2.2)
(2.2)
Числа m и n называются размерами матрицы, т.е. (2.1), (2.2) – записи матрицы размеров m на n (m строк и n столбцов).
Опр. 2. Если число строк матрицы совпадает с числом столбцов, т.е. m = n, то матрица называется квадратной порядка n.
Опр.
3.
Матрица, в которой столбцы заменены
строками, а строки столбцами, называется
транспонированной
и обозначается
 .
.
Опр.
4.
Элементы квадратной матрицы с одинаковыми
индексами называются главной диагональю,
т.е. элементами главной диагонали будут:

Транспонированная матрица получается из матрицы А поворотом на 180° относительно главной диагонали. Например,
если

1.5. Действия над матрицами
Рассмотрим
две матрицы одинаковых размеров m n:
,
n:
,
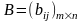 .
Обозначим через I множество, состоящее
из первых m чисел натурального ряда,
т.е.
.
Обозначим через I множество, состоящее
из первых m чисел натурального ряда,
т.е.
I = {1, 2, ..., m}.
Опр.5 Матрицы А и В называются равными, если
 ,
,
т.e. в которых равны элементы, стоящие на одинаковых местах.
Обозначается: А = В.
Опр. 6. Суммой матриц А и В называется матрица
 ,
элементы которой определяются по
формулам:
,
элементы которой определяются по
формулам:

т.e. элементы матрицы С равны сумме соответствующих элементов матриц А и В.
Обозначается: С = А + В.
Опр. 7.Произведением матрицы А на действительное число называется матрица , элементы которой вычисляются по формуле:

т.е. каждый элемент матрицы А умножается на число .
Обозначается:
 .
.
Пусть
теперь
 ,
,
 ,
т.е. число столбцов матрицы А совпадает
с числом строк матрицы В.
,
т.е. число столбцов матрицы А совпадает
с числом строк матрицы В.
Опр8. Произведением матрицы А на матрицу В называется матрица размера m n , элементы которой вычисляются по формуле:
 ,
,
т.е.
элемент матрицы С с номерами i и j равен
сумме попарных произведений элементов
i-й строки матрицы А на соответствующие
элементы j-го столбца матрицы В (правило
«строка на столбец»). Обозначается:
 .
.
Например,
если
 то элементы матрицы
будут равны:
то элементы матрицы
будут равны:





 ,
,
таким образом
 .
.
Произведение
матриц не коммутативно (не перестановочно)!,
т.е., вообще говоря,
 .
.
Опр.
9.
если все-таки
 ,
то матрицы А и В называются
перестановочными.
,
то матрицы А и В называются
перестановочными.
Опр.10. Квадратная матрица, у которой элементы, стоящие на главной диагонали равны 1, а все остальные равны 0, называется единичной и обозначается: Е.
Единичная
матрица перестановочна с любой квадратной
матрицей порядка n, так как нетрудно
убедиться, что
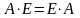 .
.
Опр.11. Определим понятие обратной матрицы. Оно определяется только для квадратных матриц. Далее А – квадратная матрица порядка n.
Матрица
 называется обратной
к матрице А, если
называется обратной
к матрице А, если
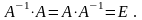
Поэтому матрицы А и называются взаимно обратными.

 (2;1)
и
(2;1)
и
 (-1;1).
Найти скалярное произведение
(-1;1).
Найти скалярное произведение
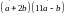
 и
и
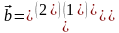 .
.
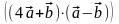

 =(3;2;0),
=(3;2;0),
 =(0;-1;1).
=(0;-1;1). =(0;-1;-2).
=(0;-1;-2).